- 数学C|空間ベクトル「空間の直線と平面の交点のベクトル」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|空間の直線と平面の交点のベクトル
空間ベクトル 31平行六面体 \(\rm ABCD-EFGH \) と辺 \(\rm AB \) の中点 \(\rm M \) について、対角線 \(\rm AG \) と \( \triangle {\rm DEM} \) との交点を \(\rm P \) とするとき、\( \overrightarrow{\rm AP} \) を \( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\)\(\overrightarrow{\rm AD}=\overrightarrow{y}~,~\)\( \overrightarrow{\rm AE}=\overrightarrow{z} \) を用いて表す方法は?
高校数学C|空間ベクトル
解法のPoint
空間の直線と平面の交点のベクトル
Point:空間の直線と平面の交点のベクトル
① 基本となる3つのベクトルを設定する。
\( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\overrightarrow{\rm AD}=\overrightarrow{y}~,~\overrightarrow{\rm AE}=\overrightarrow{z} \)
② 交点 \( \rm P \) が直線上にある条件式を立てる。
点 \( \rm P \) が直線 \( \rm AG \) 上にある
\(~\Leftrightarrow ~ \overrightarrow{\rm AP}=k\overrightarrow{\rm AG} \) となる実数 \( k \) がある
③ 交点 \( \rm P \) が平面上にある条件式を立てる。
点 \( \rm P \) が平面 \( \rm DEM \) 上にある
\(~\Leftrightarrow ~ \overrightarrow{\rm DP}=s\overrightarrow{\rm DE}+t\overrightarrow{\rm DM} \) となる実数 \( s~,~t \) がある
④ 2つの条件式を①の基本ベクトルで表して、4点 \( \rm A~,~B~,~D~,~E \) が同一平面上にないことをいい、係数を比較する。
⑤ これより、\(k\) の値を求めて、比を求める。
空間において、直線と平面の交点のベクトルでの表し方は、
① 基本となる3つのベクトルを設定する。
\( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\overrightarrow{\rm AD}=\overrightarrow{y}~,~\overrightarrow{\rm AE}=\overrightarrow{z} \)
② 交点 \( \rm P \) が直線上にある条件式を立てる。
点 \( \rm P \) が直線 \( \rm AG \) 上にある
\(~\Leftrightarrow ~ \overrightarrow{\rm AP}=k\overrightarrow{\rm AG} \) となる実数 \( k \) がある
③ 交点 \( \rm P \) が平面上にある条件式を立てる。
点 \( \rm P \) が平面 \( \rm DEM \) 上にある
\(~\Leftrightarrow ~ \overrightarrow{\rm DP}=s\overrightarrow{\rm DE}+t\overrightarrow{\rm DM} \) となる実数 \( s~,~t \) がある
④ 2つの条件式を①の基本ベクトルで表して、4点 \( \rm A~,~B~,~D~,~E \) が同一平面上にないことをいい、係数を比較する。
⑤ これより、\(k\) の値を求めて、比を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|空間の直線と平面の交点のベクトル
空間ベクトル 31
平行六面体 \(\rm ABCD-EFGH \) と辺 \(\rm AB \) の中点 \(\rm M \) について、対角線 \(\rm AG \) と \( \triangle {\rm DEM} \) との交点を \(\rm P \) とするとき、\( \overrightarrow{\rm AP} \) を \( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\)\(\overrightarrow{\rm AD}=\overrightarrow{y}~,~\)\( \overrightarrow{\rm AE}=\overrightarrow{z} \) を用いて表す方法は?
高校数学C|空間ベクトル
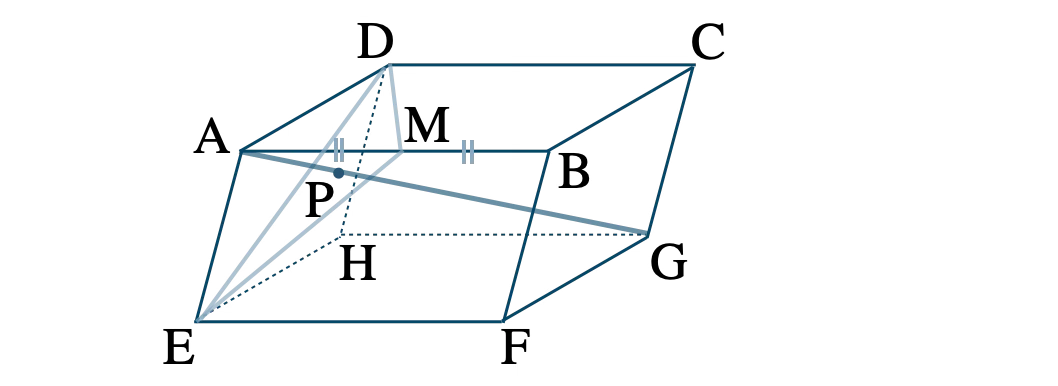
\( \overrightarrow{\rm AB}=\overrightarrow{x}~,~\overrightarrow{\rm AD}=\overrightarrow{y}~,~\overrightarrow{\rm AE}=\overrightarrow{z} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CG}
\\[3pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AE}
\\[3pt]~~~&=&\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}
\end{eqnarray}\)
ここで、点 \( \rm P \) は直線 \( \rm AG \) 上にあるので、
\( \overrightarrow{\rm AP}=k\cdot\overrightarrow{\rm AG} \) となる実数 \( k \) がある
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&k\cdot\left(\overrightarrow{x}+\overrightarrow{y}+\overrightarrow{z}\right)
\\[3pt]~~~&=&k\overrightarrow{x}+k\overrightarrow{y}+k\overrightarrow{z}~ ~ ~ \cdots {\small [\,1\,]}
\end{eqnarray}\)
次に、点 \( \rm P \) は平面 \( \rm DEM \) 上にあるので、
\( \overrightarrow{\rm DP}=s\overrightarrow{\rm DE}+t\overrightarrow{\rm DM} \) となる実数 \( s~,~t \) がある
始点を \( \rm A \) に揃えると、
\(\begin{eqnarray}~~~\overrightarrow{\rm AP}-\overrightarrow{\rm AD}&=&s(\overrightarrow{\rm AE}-\overrightarrow{\rm AD})+t(\overrightarrow{\rm AM}-\overrightarrow{\rm AD})
\end{eqnarray}\)
ここで、\( \overrightarrow{\rm AD}=\overrightarrow{y}~,~\overrightarrow{\rm AE}=\overrightarrow{z}\) と \(\overrightarrow{\rm AM}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm AB}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{x} \) より、
\(\begin{eqnarray}~\overrightarrow{\rm AP}-\overrightarrow{y}&=&s\overrightarrow{z}-s\overrightarrow{y}+\displaystyle \frac{\,1\,}{\,2\,}t\overrightarrow{x}-t\overrightarrow{y}
\\[5pt]~\overrightarrow{\rm AP}
&=&\displaystyle \frac{\,1\,}{\,2\,}t\overrightarrow{x}+\left(1-s-t\right)\overrightarrow{y}+s\overrightarrow{z}~ ~ \cdots {\small [\,2\,]}
\end{eqnarray}\)
\({\small [\,1\,]}\) と \({\small [\,2\,]}\) より、4点 \( \rm A~,~B~,~D~,~E \) は同一平面上にないので、
\(\begin{eqnarray}~~~ \left\{~\begin{array}{l}
k=\displaystyle \frac{\,1\,}{\,2\,}t \hspace{21pt}~ ~ ~ \cdots {\small [\,3\,]} \\[5pt] k=1-s-t ~ ~ ~ \cdots {\small [\,4\,]}\\[5pt] k=s \hspace{33pt}~ ~ ~ \cdots {\small [\,5\,]}
\end{array}\right.\end{eqnarray}\)
\({\small [\,3\,]}\) より \( t=2k \) 、\({\small [\,5\,]}\) より \( s=k \) を \({\small [\,4\,]}\) に代入すると、
\(\begin{eqnarray}~~~k&=&1-k-2k
\\[3pt]~~~4k&=&1
\\[5pt]~~~k&=&\displaystyle \frac{\,1\,}{\,4\,}
\end{eqnarray}\)
したがって、\({\small [\,1\,]}\) より
\( \overrightarrow{\rm AP}=\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{x}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{y}+\displaystyle \frac{\,1\,}{\,4\,}\overrightarrow{z} \)



