- 数学C|平面上のベクトル「ベクトルの大きさと等しいベクトル」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|ベクトルの大きさと等しいベクトル
平面上のベクトル 01ベクトルの大きさは何を表すか?また、あるベクトルと等しいベクトル or 向きが同じベクトル or 逆ベクトルとは?さらに、零ベクトルとは?
高校数学C|平面上のベクトル
解法のPoint
ベクトルの大きさと等しいベクトル
Point:ベクトルの大きさと等しいベクトル
ベクトルは始点と終点を用いて \(\overrightarrow{\rm AB}\) と表すか、1つの文字を用いて \(\overrightarrow{a}\) と表す。

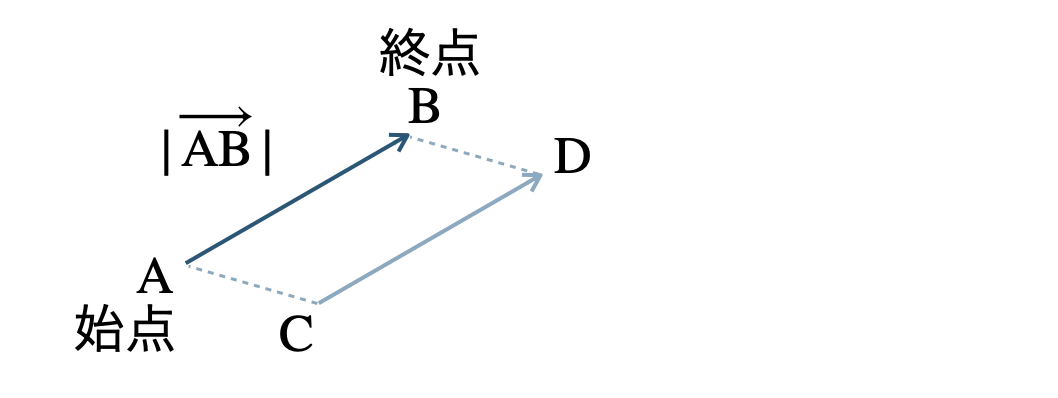
■ ベクトルの大きさ
その線分の長さで、\(|\,\overrightarrow{\rm AB}\,|\) や \(|\,\overrightarrow{a}\,|\) と表す。
■ 等しいベクトル
向きも大きさも等しいベクトルであり、
\(\overrightarrow{\rm AB}=\overrightarrow{\rm CD}\) や \(\overrightarrow{a}=\overrightarrow{b}\) と表す。
※ 平行移動で重なるベクトル
■ 向きが同じベクトル
平行で向きが同じベクトル。
※ 大きさは一致しなくてもよい。
■ 逆ベクトル
大きさが等しく、向きが反対のベクトル。
\(\overrightarrow{a}\) の逆ベクトルは \(-\overrightarrow{a}\)
\(\overrightarrow{\rm AB}\) の逆ベクトルは \(-\overrightarrow{\rm AB}=\overrightarrow{\rm BA}\)
■ 零ベクトル
始点と終点が一致するベクトルで、
大きさは \(0\) であり、\(\overrightarrow{0}\) と表す。
・点 \(\rm A\) において、\(\overrightarrow{\rm AA}=\overrightarrow{0}\)
・\(\overrightarrow{a}\) と 逆ベクトル \(-\overrightarrow{a}\) の和は零ベクトル
\(\overrightarrow{a}+(-\overrightarrow{a})=\overrightarrow{0}\)
・零ベクトルとの和 \(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\)
矢印のついた線分を「有向線分」といい、有向線分の「向き」と「大きさ」だけに注目した量を「ベクトル」という。
ベクトルは始点と終点を用いて \(\overrightarrow{\rm AB}\) と表すか、1つの文字を用いて \(\overrightarrow{a}\) と表す。


■ ベクトルの大きさ
その線分の長さで、\(|\,\overrightarrow{\rm AB}\,|\) や \(|\,\overrightarrow{a}\,|\) と表す。
■ 等しいベクトル
向きも大きさも等しいベクトルであり、
\(\overrightarrow{\rm AB}=\overrightarrow{\rm CD}\) や \(\overrightarrow{a}=\overrightarrow{b}\) と表す。
※ 平行移動で重なるベクトル
■ 向きが同じベクトル
平行で向きが同じベクトル。
※ 大きさは一致しなくてもよい。
■ 逆ベクトル
大きさが等しく、向きが反対のベクトル。
\(\overrightarrow{a}\) の逆ベクトルは \(-\overrightarrow{a}\)
\(\overrightarrow{\rm AB}\) の逆ベクトルは \(-\overrightarrow{\rm AB}=\overrightarrow{\rm BA}\)
■ 零ベクトル
始点と終点が一致するベクトルで、
大きさは \(0\) であり、\(\overrightarrow{0}\) と表す。
・点 \(\rm A\) において、\(\overrightarrow{\rm AA}=\overrightarrow{0}\)
・\(\overrightarrow{a}\) と 逆ベクトル \(-\overrightarrow{a}\) の和は零ベクトル
\(\overrightarrow{a}+(-\overrightarrow{a})=\overrightarrow{0}\)
・零ベクトルとの和 \(\overrightarrow{a}+\overrightarrow{0}=\overrightarrow{a}\)
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|ベクトルの大きさと等しいベクトル
平面上のベクトル 01
ベクトルの大きさは何を表すか?また、あるベクトルと等しいベクトル or 向きが同じベクトル or 逆ベクトルとは?さらに、零ベクトルとは?
高校数学C|平面上のベクトル
ベクトルの大きさは、その線分の長さを表す
等しいベクトルは、向きも大きさも等しいベクトル
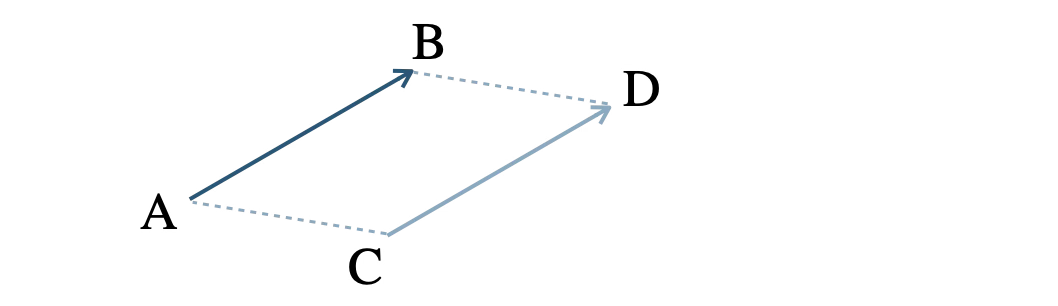

\(\overrightarrow{\rm AB}=\overrightarrow{\rm CD}\)
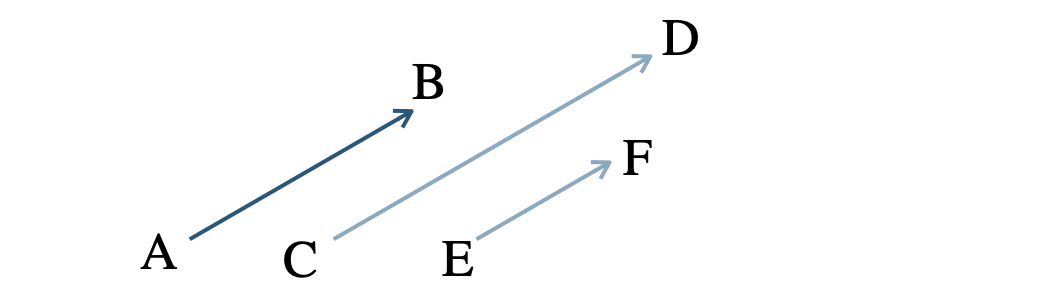
向きが同じベクトルは、平行で向きが同じベクトル
※ 大きさは一致しなくてもよい。
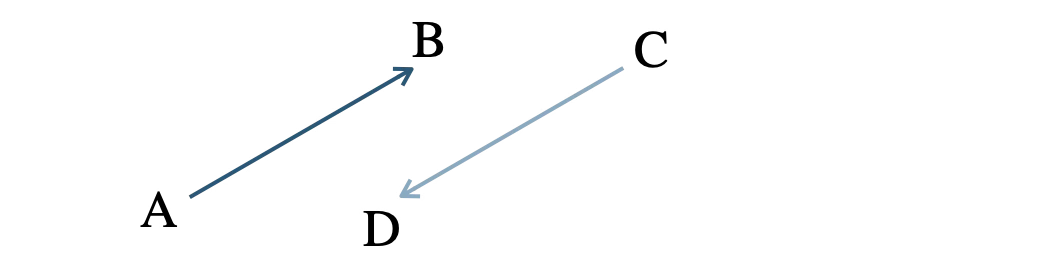
逆ベクトルは、大きさが等しく、向きが反対のベクトル

零ベクトル \(\overrightarrow{0}\) は、始点と終点が一致するベクトルで大きさは \(0\) である


