- 数学C|平面上のベクトル「正六角形における内積」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|正六角形における内積
高校数学C|平面上のベクトル
解法のPoint
正六角形における内積
1辺の長さ \(2\) の正六角形の内積の求め方は、


内部を対角線で6つの正三角形に分ける。
このとき、それぞれの正三角形の各辺の長さは \(2\) となり、内角はすべて等しく \(60^\circ\) となる。また、頂点から下ろした垂線の長さは \(\sqrt{3}\) となる。
これより、大きさやなす角を調べて、内積の値を求める。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|正六角形における内積
1辺の長さ \(2\) の正六角形 \(\rm ABCDEF\) において、内積 \(\overrightarrow{\rm AB} \cdot \overrightarrow{\rm AF}~,~\)\(\overrightarrow{\rm AB} \cdot \overrightarrow{\rm AE}~,~\)\(\overrightarrow{\rm AB} \cdot \overrightarrow{\rm AD}~,~\)\(\overrightarrow{\rm AB} \cdot \overrightarrow{\rm AC}~,~\)\(\overrightarrow{\rm AC} \cdot \overrightarrow{\rm AE}~,~\)\(\overrightarrow{\rm AD} \cdot \overrightarrow{\rm CE}\) の求め方は?
高校数学C|平面上のベクトル
内積 \(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AF}\) は、


\(|\,\overrightarrow{\rm AB}\,|=2~,~|\,\overrightarrow{\rm AF}\,|=2\)、なす角 \(\theta=120^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AF}&=&|\,\overrightarrow{\rm AB}\,|\,|\,\overrightarrow{\rm AF}\,|\cos120^\circ
\\[5pt]~~~&=&2{\, \small \times \,}2{\, \small \times \,}\left(\,-\displaystyle\frac{\,1\,}{\,2\,}\,\right)
\\[5pt]~~~&=&-2
\end{eqnarray}\)
内積 \(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AE}\) は、


\(|\,\overrightarrow{\rm AB}\,|=2~,~|\,\overrightarrow{\rm AE}\,|=2\sqrt{3}\)、なす角 \(\theta=90^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AE}&=&|\,\overrightarrow{\rm AB}\,|\,|\,\overrightarrow{\rm AE}\,|\cos90^\circ
\\[5pt]~~~&=&2{\, \small \times \,}2\sqrt{3}{\, \small \times \,}0
\\[5pt]~~~&=&0
\end{eqnarray}\)
内積 \(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AD}\) は、


\(|\,\overrightarrow{\rm AB}\,|=2~,~|\,\overrightarrow{\rm AD}\,|=4\)、なす角 \(\theta=60^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AD}&=&|\,\overrightarrow{\rm AB}\,|\,|\,\overrightarrow{\rm AD}\,|\cos60^\circ
\\[5pt]~~~&=&2{\, \small \times \,}4{\, \small \times \,}\displaystyle\frac{\,1\,}{\,2\,}
\\[5pt]~~~&=&4
\end{eqnarray}\)
内積 \(\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}\) は、
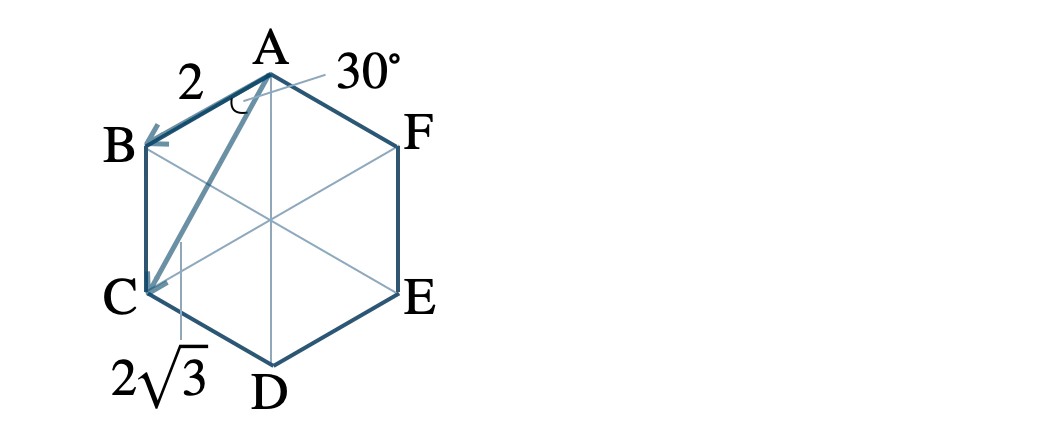

\(|\,\overrightarrow{\rm AB}\,|=2~,~|\,\overrightarrow{\rm AC}\,|=2\sqrt{3}\)、なす角 \(\theta=30^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}&=&|\,\overrightarrow{\rm AB}\,|\,|\,\overrightarrow{\rm AC}\,|\cos30^\circ
\\[5pt]~~~&=&2{\, \small \times \,}2\sqrt{3}{\, \small \times \,}\displaystyle\frac{\,\sqrt{3}\,}{\,2\,}
\\[5pt]~~~&=&2{\, \small \times \,}3=6
\end{eqnarray}\)
内積 \(\overrightarrow{\rm AC}\cdot\overrightarrow{\rm AE}\) は、


\(|\,\overrightarrow{\rm AC}\,|=2\sqrt{3}~,~|\,\overrightarrow{\rm AE}\,|=2\sqrt{3}\)、なす角 \(\theta=60^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AC}\cdot\overrightarrow{\rm AE}&=&|\,\overrightarrow{\rm AC}\,|\,|\,\overrightarrow{\rm AE}\,|\cos60^\circ
\\[5pt]~~~&=&2\sqrt{3}{\, \small \times \,}2\sqrt{3}{\, \small \times \,}\displaystyle\frac{\,1\,}{\,2\,}
\\[5pt]~~~&=&2{\, \small \times \,}3=6
\end{eqnarray}\)
内積 \(\overrightarrow{\rm AD}\cdot\overrightarrow{\rm CE}\) は、
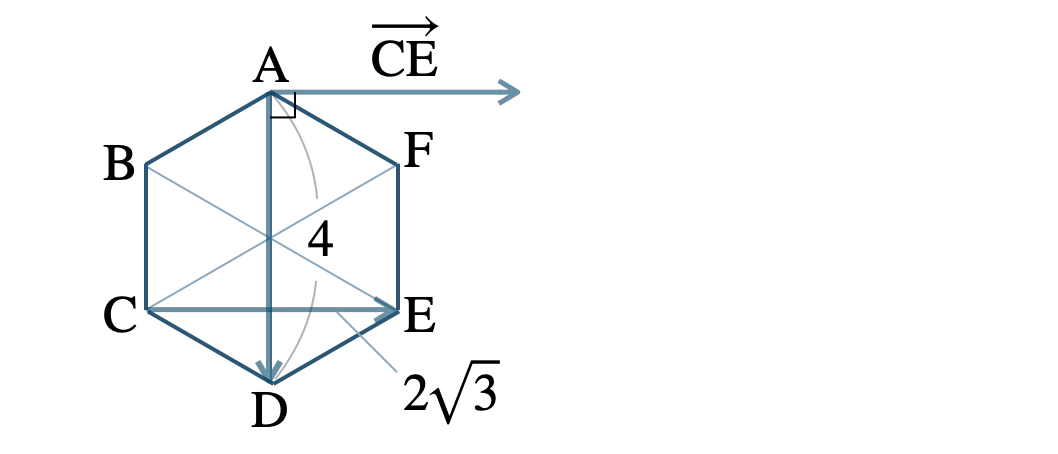
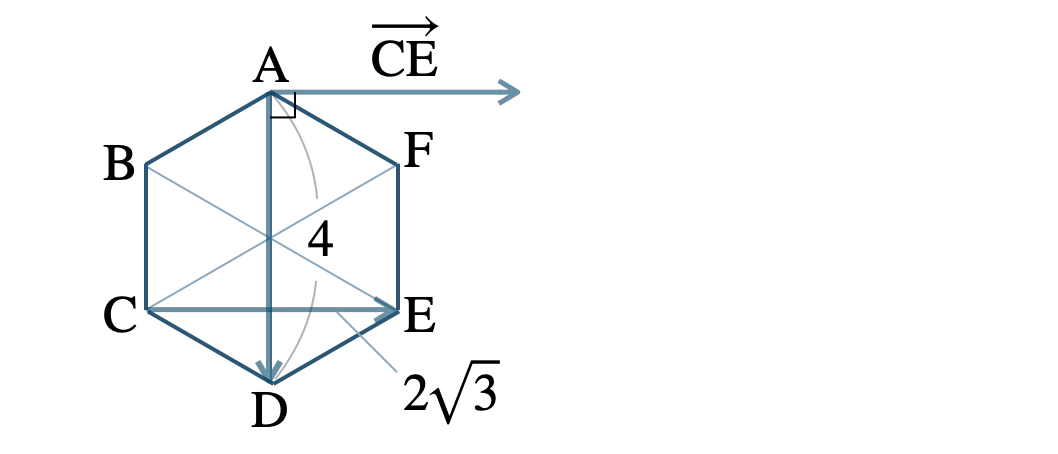
\(|\,\overrightarrow{\rm AD}\,|=4~,~|\,\overrightarrow{\rm CE}\,|=2\sqrt{3}\)、
\(\overrightarrow{\rm CE}\) の始点を \({\rm A}\) に揃えると、なす角 \(\theta=90^\circ\)
よって、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}\cdot\overrightarrow{\rm CE}&=&|\,\overrightarrow{\rm AD}\,|\,|\,\overrightarrow{\rm CE}\,|\cos90^\circ
\\[5pt]~~~&=&4{\, \small \times \,}2\sqrt{3}{\, \small \times \,}0
\\[5pt]~~~&=&0
\end{eqnarray}\)



