このページは、「係数の和が一定の範囲の点の存在範囲」の練習問題アーカイブページとなります。
この問題の解き方の詳細は↓
係数の和が一定の範囲の点の存在範囲 で確認できます。
問題アーカイブ01
問題アーカイブ01\(\triangle {\rm OAB}\) に対して、点 \({\rm P}\) が \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~\)\(0{\small ~≦~}s+t{\small ~≦~}2~,~\)\(s{\small ~≧~}0~,~\)\(t{\small ~≧~}0\) を満たしながら動くとき、点 \(\rm P\) の存在範囲を求めよ。
数研出版|数学C[708] p.42 問12
数研出版|高等学校数学C[709] p.42 練習35(1)
\(0{\small ~≦~}s+t{\small ~≦~}2\) より、各辺を \(\displaystyle \frac{\,1\,}{\,2\,}\) 倍すると、
\(~~~0{\small ~≦~}\displaystyle \frac{\,1\,}{\,2\,}s+\displaystyle \frac{\,1\,}{\,2\,}t{\small ~≦~}1\)
ここで、\(s^{\prime}=\displaystyle \frac{\,1\,}{\,2\,}s~,~t^{\prime}=\displaystyle \frac{\,1\,}{\,2\,}t\) とおくと、
\(~0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1\)
また、\(s=2s^{\prime}~,~t=2t^{\prime}\) より、
\(~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~\overrightarrow{\rm OP}&=&s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}
\\[5pt]~&=&2s^{\prime}\overrightarrow{\rm OA}+2t^{\prime}\overrightarrow{\rm OB}
\\[5pt]~~~&=&s^{\prime}\left(2\overrightarrow{\rm OA}\right)+t^{\prime}\left(2\overrightarrow{\rm OB}\right)
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OA^{\prime}}=2\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=2\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、

\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は \(\triangle {\rm OA^{\prime}B^{\prime}}\) の周および内部となる
問題アーカイブ02
問題アーカイブ02\(\triangle {\rm OAB}\) に対して、点 \({\rm P}\) が \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,\)\(0{\small ~≦~}s+t{\small ~≦~}3~,~\)\(s{\small ~≧~}0~,~\)\(t{\small ~≧~}0\) を満たしながら動くとき、点 \(\rm P\) の存在範囲を求めよ。
数研出版|数学C[708] p.42 練習30(2)
\(0{\small ~≦~}s+t{\small ~≦~}3\) より、各辺を \(\displaystyle \frac{\,1\,}{\,3\,}\) 倍すると、
\(~~~0{\small ~≦~}\displaystyle \frac{\,1\,}{\,3\,}s+\displaystyle \frac{\,1\,}{\,3\,}t{\small ~≦~}1\)
ここで、\(s^{\prime}=\displaystyle \frac{\,1\,}{\,3\,}s~,~t^{\prime}=\displaystyle \frac{\,1\,}{\,3\,}t\) とおくと、
\(~0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1\)
また、\(s=3s^{\prime}~,~t=3t^{\prime}\) より、
\(~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~\overrightarrow{\rm OP}&=&s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}
\\[5pt]~&=&3s^{\prime}\overrightarrow{\rm OA}+3t^{\prime}\overrightarrow{\rm OB}
\\[5pt]~~~&=&s^{\prime}\left(3\overrightarrow{\rm OA}\right)+t^{\prime}\left(3\overrightarrow{\rm OB}\right)
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OA^{\prime}}=3\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=3\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、

\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は \(\triangle {\rm OA^{\prime}B^{\prime}}\) の周および内部となる
問題アーカイブ03
問題アーカイブ03\(\triangle {\rm OAB}\) に対して、点 \({\rm P}\) が \(\overrightarrow{\rm OP}=s\overrightarrow{\rm OA}+t\overrightarrow{\rm OB}~,~\)\(1{\small ~≦~}s+t{\small ~≦~}3~,~\)\(s{\small ~≧~}0~,~\)\(t{\small ~≧~}0\) を満たしながら動くとき、点 \(\rm P\) の存在範囲を求めよ。
数研出版|数学C[708] p.49 演習問題B 7(2)
\(1{\small ~≦~}s+t{\small ~≦~}3\) より、各辺を \(\displaystyle \frac{\,1\,}{\,3\,}\) 倍すると、
\(~~~\displaystyle \frac{\,1\,}{\,3\,}{\small ~≦~}\displaystyle \frac{\,1\,}{\,3\,}s+\displaystyle \frac{\,1\,}{\,3\,}t{\small ~≦~}1\)
ここで、\(s^{\prime}=\displaystyle \frac{\,1\,}{\,3\,}s~,~t^{\prime}=\displaystyle \frac{\,1\,}{\,3\,}t\) とおくと、
\(~\displaystyle \frac{\,1\,}{\,3\,}{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1\)
また、\(s=3s^{\prime}~,~t=3t^{\prime}\) より、
\(~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~\overrightarrow{\rm OP}&=&s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}
\\[5pt]~&=&3s^{\prime}\overrightarrow{\rm OA}+3t^{\prime}\overrightarrow{\rm OB}
\\[5pt]~~~&=&s^{\prime}\left(3\overrightarrow{\rm OA}\right)+t^{\prime}\left(3\overrightarrow{\rm OB}\right)
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OA^{\prime}}=3\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=3\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、

\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&\displaystyle \frac{\,1\,}{\,3\,}{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は台形 \({\rm AA^{\prime}B^{\prime}}B\) の周および内部となる
問題アーカイブ04
問題アーカイブ04\(\triangle {\rm OAB}\) に対して、\(\overrightarrow{\rm OP}=s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}\) とおく。実数 \(s~,~t\) が、\(s{\small ~≧~}0~,~\)\(t{\small ~≧~}0~,~\)\(s+t{\small ~≦~}\displaystyle \frac{\,1\,}{\,2\,}\) を満たしながら変化するとき、点 \({\rm P}\) の存在する範囲を求めよ。
東京書籍|Advanced数学C[701] p.39 問12
東京書籍|Standard数学C[702] p.44 Challenge 問1
\(0{\small ~≦~}s+t{\small ~≦~}\displaystyle \frac{\,1\,}{\,2\,}\) より、各辺を \(2\) 倍すると、
\(~~~0{\small ~≦~}2s+2t{\small ~≦~}1\)
ここで、\(s^{\prime}=2s~,~t^{\prime}=2t\) とおくと、
\(~0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1\)
また、\(s=\displaystyle \frac{\,s^{\prime}\,}{\,2\,}~,~t=\displaystyle \frac{\,t^{\prime}\,}{\,2\,}\) より、
\(~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~\overrightarrow{\rm OP}&=&s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}
\\[5pt]~&=&\displaystyle \frac{\,s^{\prime}\,}{\,2\,}\overrightarrow{\rm OA}+\displaystyle \frac{\,t^{\prime}\,}{\,2\,}\overrightarrow{\rm OB}
\\[5pt]~~~&=&s^{\prime}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}\right)+t^{\prime}\left(\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OB}\right)
\end{eqnarray}\)
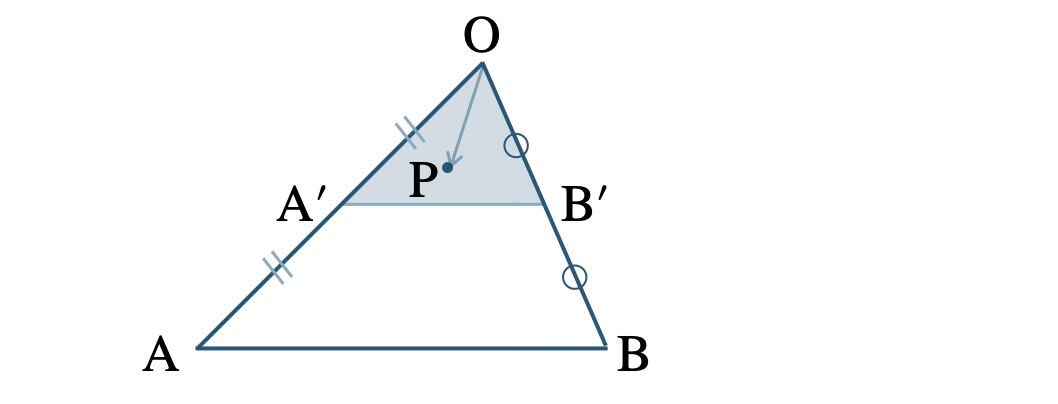
ここで、\(\overrightarrow{\rm OA^{\prime}}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=\displaystyle \frac{\,1\,}{\,2\,}\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、
\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は \(\triangle {\rm OA^{\prime}B^{\prime}}\) の周および内部となる
問題アーカイブ05
問題アーカイブ05\({\rm O}\) を原点とする座標平面上に \(2\) 点 \({\rm A}(1\,,\,0)\)、\({\rm B}(0\,,\,1)\) がある。点 \({\rm P}\) が \(\overrightarrow{\rm OP}=s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}\) で表され、実数 \(s~,~t\) が \(s{\small ~≧~}0~,~\)\(t{\small ~≧~}0~,~\)\(s+t{\small ~≦~}2\) を満たしながら変化するとき、点 \({\rm P}\) の存在範囲を図示せよ。
東京書籍|Advanced数学C[701] p.39 問13
\(0{\small ~≦~}s+t{\small ~≦~}2\) より、各辺を \(\displaystyle \frac{\,1\,}{\,2\,}\) 倍すると、
\(~~~0{\small ~≦~}\displaystyle \frac{\,s\,}{\,2\,}+\displaystyle \frac{\,t\,}{\,2\,}{\small ~≦~}1\)
ここで、\(s^{\prime}=\displaystyle \frac{\,s\,}{\,2\,}~,~t^{\prime}=\displaystyle \frac{\,t\,}{\,2\,}\) とおくと、
\(~0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1\)
また、\(s=2s^{\prime}~,~t=2t^{\prime}\) より、
\(~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\)
次に、\(\overrightarrow{\rm OP}\) は、
\(\begin{eqnarray}~\overrightarrow{\rm OP}&=&s\,\overrightarrow{\rm OA}+t\,\overrightarrow{\rm OB}
\\[5pt]~&=&2s^{\prime}\overrightarrow{\rm OA}+2t^{\prime}\overrightarrow{\rm OB}
\\[5pt]~~~&=&s^{\prime}\left(2\overrightarrow{\rm OA}\right)+t^{\prime}\left(2\overrightarrow{\rm OB}\right)
\end{eqnarray}\)
ここで、\(\overrightarrow{\rm OA^{\prime}}=2\overrightarrow{\rm OA}~,~\overrightarrow{\rm OB^{\prime}}=2\overrightarrow{\rm OB}\) を満たす点 \(\rm A^{\prime}~,~B^{\prime}\) をとると、
\({\rm A}(1\,,\,0)\) より \({\rm A^{\prime}}(2\,,\,0)\)、\({\rm B}(0\,,\,1)\) より \({\rm B^{\prime}}(0\,,\,2)\)

\(\begin{eqnarray}&&\overrightarrow{\rm OP}=s^{\prime}\overrightarrow{\rm OA^{\prime}}+t^{\prime}\overrightarrow{\rm OB^{\prime}}
\\[3pt]&&0{\small ~≦~}s^{\prime}+t^{\prime}{\small ~≦~}1~,~s^{\prime}{\small ~≧~}0~,~t^{\prime}{\small ~≧~}0\end{eqnarray}\)
これより、点 \(\rm P\) の存在範囲は \(\triangle {\rm OA^{\prime}B^{\prime}}\) の周および内部となる


