- 数学C|空間ベクトル「平行六面体とベクトルの実数倍」の基本例題解説ページです。
- 目次をクリックすると各セクションへ移動します。
問題|平行六面体とベクトルの実数倍
高校数学C|空間ベクトル
解法のPoint
平行六面体とベクトルの実数倍
空間において、\( \overrightarrow{a}\ne \overrightarrow{0}~,~\overrightarrow{b}\ne \overrightarrow{0} \) のとき、
\( \overrightarrow{a} \,/\,/\, \overrightarrow{b} \)
\(~\Leftrightarrow ~ \overrightarrow{b}=k\overrightarrow{a} \) となる実数 \(k\) がある
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
\( \overrightarrow{\rm OA}=\overrightarrow{a}~,~\overrightarrow{\rm OB}=\overrightarrow{b}~,~\overrightarrow{\rm OC}=\overrightarrow{c} \)
とおくとき、
空間の任意のベクトル \( \overrightarrow{p} \) は、実数 \( s~,~t~,~u \) を用いて、
\( \overrightarrow{p}=s\overrightarrow{a}+t\overrightarrow{b}+u\overrightarrow{c} \)
とただ1通りに表すことができる。
©︎ 2026 教科書より詳しい高校数学 yorikuwa.com
詳しい解説|平行六面体とベクトルの実数倍
高校数学C|空間ベクトル
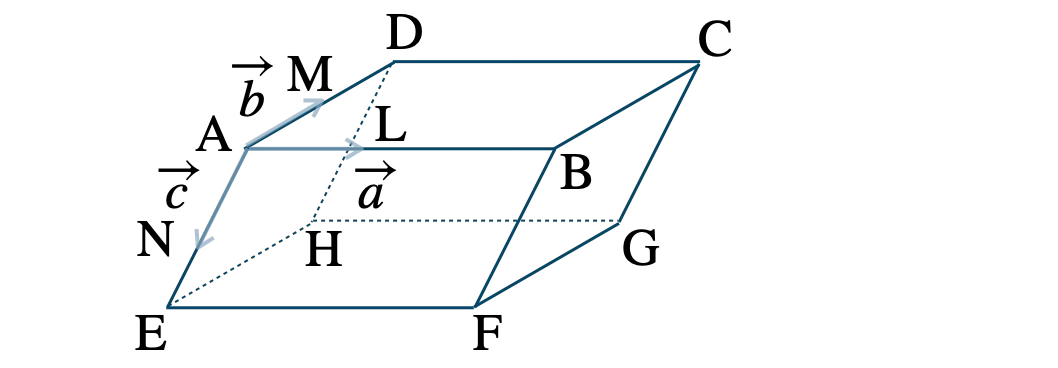
\( \overrightarrow{\rm AB} \) を \( 1:3 \) に内分する点を \( \rm L \) として、\( \overrightarrow{\rm AL}=\overrightarrow{a} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AB}&=&4\overrightarrow{\rm AL}=4\overrightarrow{a}\end{eqnarray}\)
\( \overrightarrow{\rm AD} \) の中点を \( \rm M \) として、\( \overrightarrow{\rm AM}=\overrightarrow{b} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AD}&=&2\overrightarrow{\rm AM}=2\overrightarrow{b}\end{eqnarray}\)
\( \overrightarrow{\rm AE} \) を \( 2:1 \) に内分する点を \( \rm N \) として、\( \overrightarrow{\rm AN}=\overrightarrow{c} \) より、
\(\begin{eqnarray}~~~\overrightarrow{\rm AE}&=&\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{\rm AN}=\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{c}\end{eqnarray}\)
\(\overrightarrow{\rm AC}\) は、点 \({\rm A}\) → \({\rm B}\) → \({\rm C}\) と進んでいき、
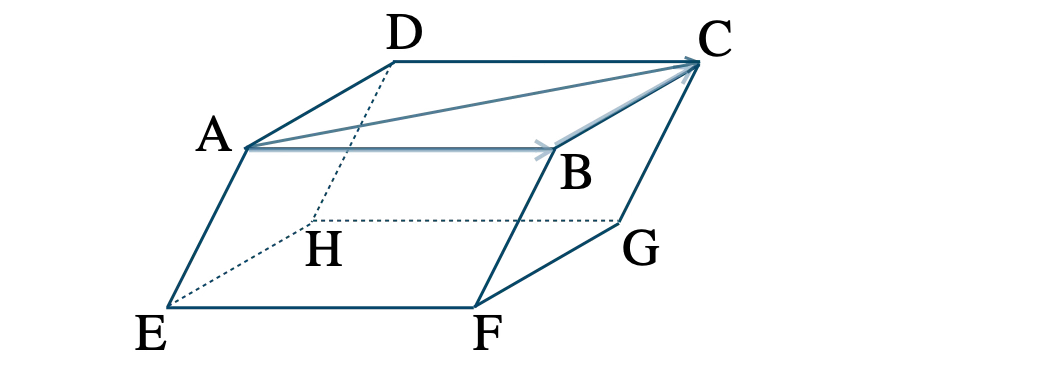

\(\begin{eqnarray}~~~\overrightarrow{\rm AC}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}
\\[5pt]~~~&=&4\overrightarrow{a}+2\overrightarrow{b}\end{eqnarray}\)
\(\overrightarrow{\rm AG}\) は、点 \({\rm A}\) → \({\rm B}\) → \({\rm C}\) → \({\rm G}\) と進んでいき、
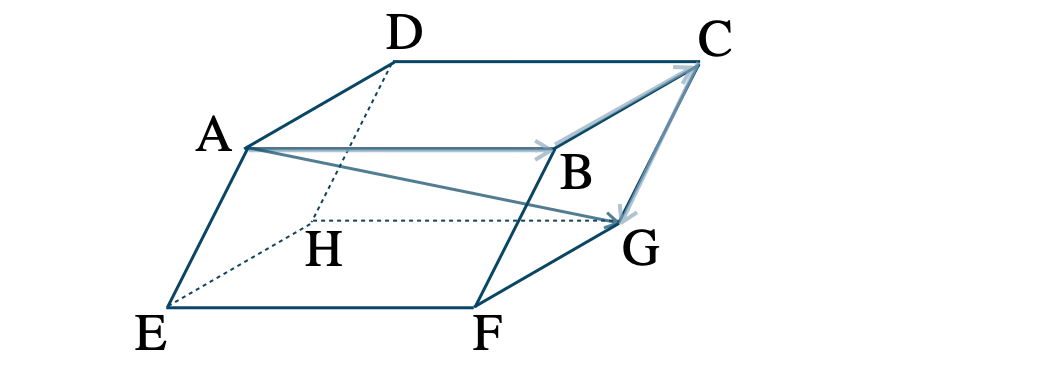

\(\begin{eqnarray}~~~\overrightarrow{\rm AG}&=&\overrightarrow{\rm AB}+\overrightarrow{\rm BC}+\overrightarrow{\rm CG}
\\[5pt]~~~&=&\overrightarrow{\rm AB}+\overrightarrow{\rm AD}+\overrightarrow{\rm AE}
\\[5pt]~~~&=&4\overrightarrow{a}+2\overrightarrow{b}+\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{c}\end{eqnarray}\)
\(\overrightarrow{\rm HB}\) は、点 \({\rm H}\) → \({\rm G}\) → \({\rm F}\) → \({\rm B}\) と進んでいき、
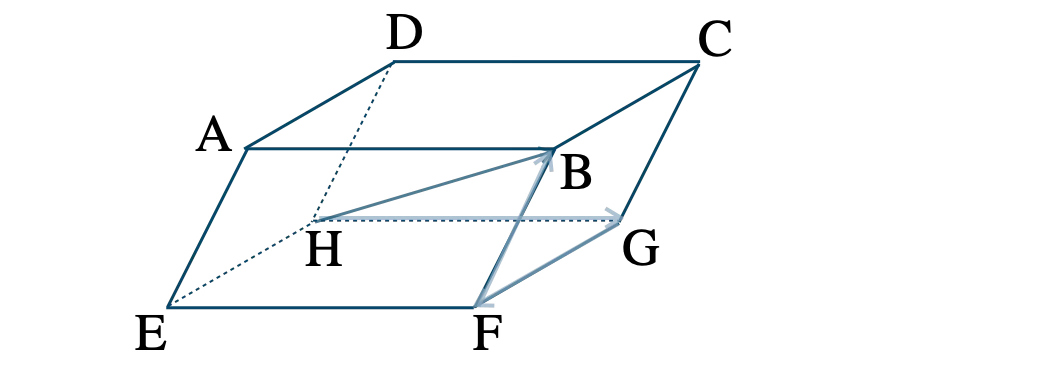

\(\begin{eqnarray}~~~\overrightarrow{\rm HB}&=&\overrightarrow{\rm HG}+\overrightarrow{\rm GF}+\overrightarrow{\rm FB}
\\[5pt]~~~&=&\overrightarrow{\rm AB}-\overrightarrow{\rm AD}-\overrightarrow{\rm AE}
\\[5pt]~~~&=&4\overrightarrow{a}-2\overrightarrow{b}-\displaystyle \frac{\,3\,}{\,2\,}\overrightarrow{c}\end{eqnarray}\)



