【新課程】数研出版：新編数学Ⅲ[710]

p.8 練習1\({\small (1)}~\)

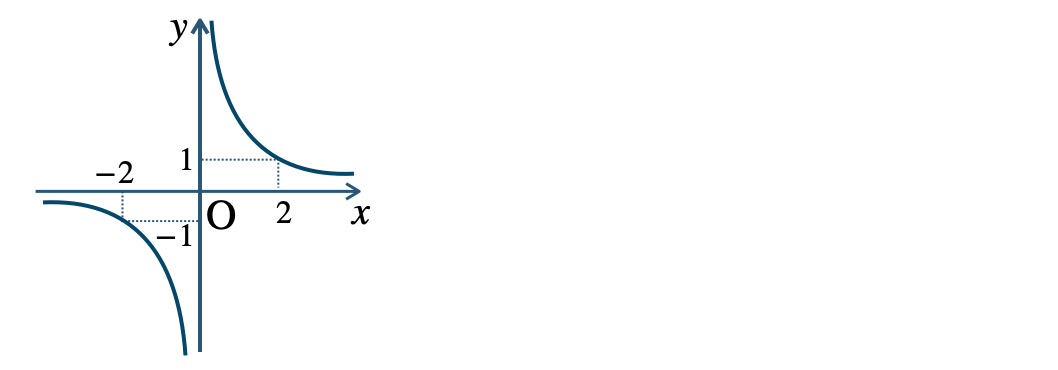
\({\small (2)}~\)

p.9 練習2\({\small (1)}~\)定義域 \(x\neq 2\)、値域 \(y\neq -1\)

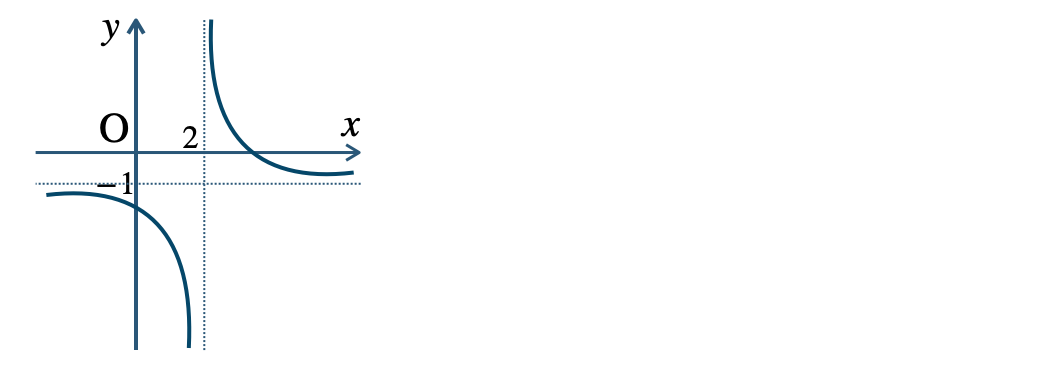
\({\small (2)}~\)定義域 \(x\neq 0\)、値域 \(y\neq 1\)

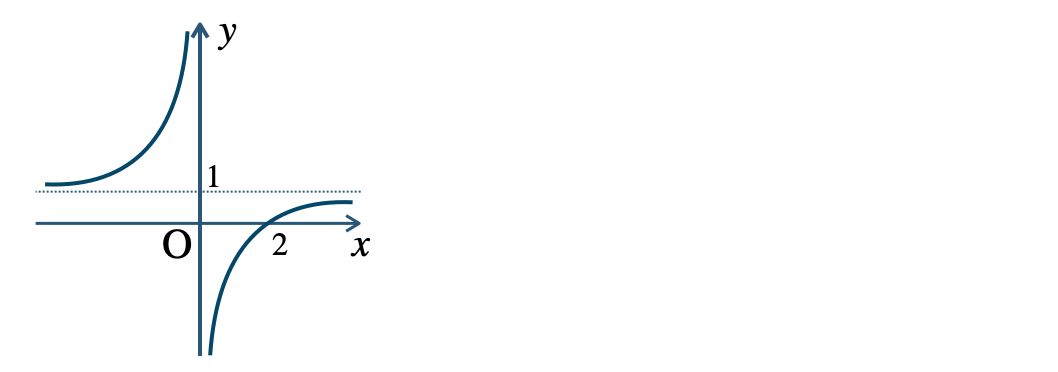
\({\small (3)}~\)定義域 \(x\neq -1\)、値域 \(y\neq -3\)

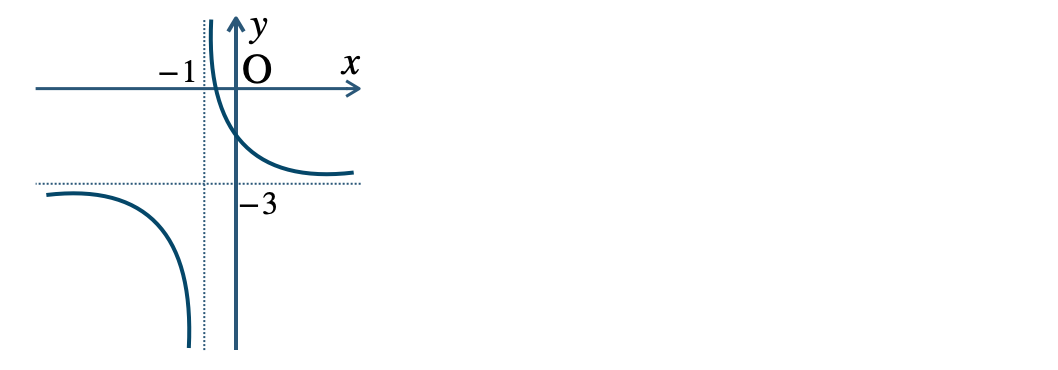
p.10 練習3\({\small (1)}~\)定義域 \(x\neq -1\)、値域 \(y\neq 3\)

\({\small (2)}~\)定義域 \(x\neq 1\)、値域 \(y\neq -2\)

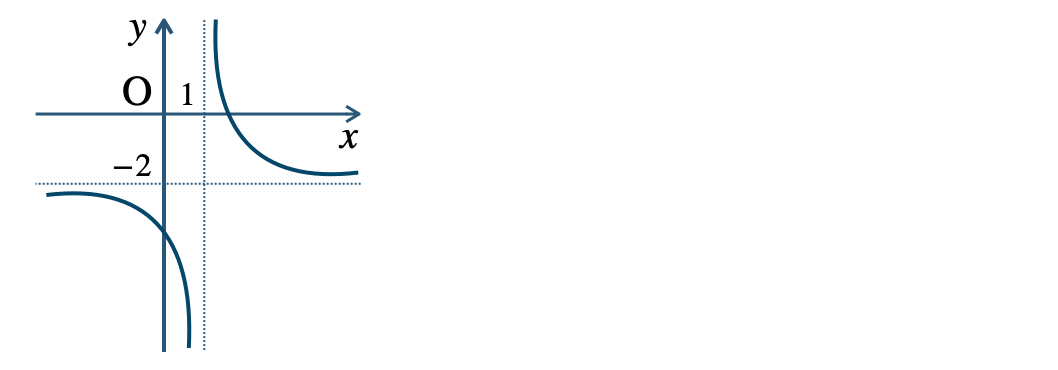
\({\small (3)}~\)定義域 \(x\neq -2\)、値域 \(y\neq 2\)

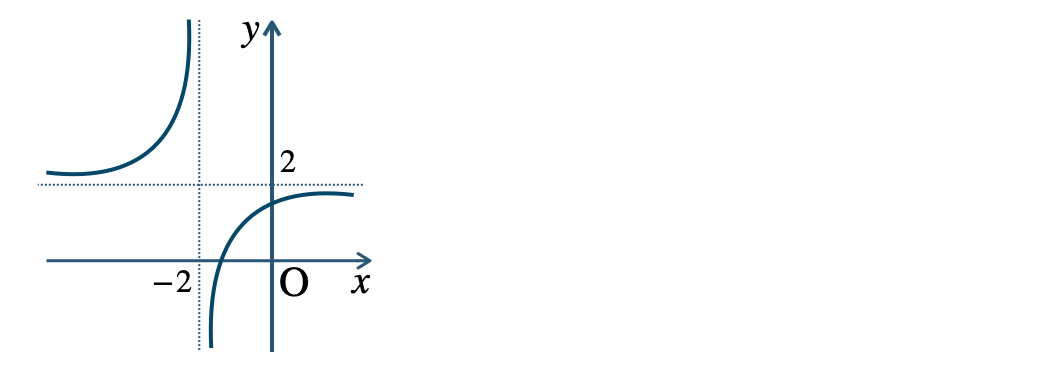
p.11 練習4$${\small (1)}~(2~,~1)~,~(-2~,~-3)$$$${\small (2)}~(2~,~1)~,~\left(-3~,~-\frac{\,3\,}{\,2\,}\right)$$$${\small (3)}~(-2~,~-3)$$

p.11 練習5$${\small (1)}~-1< x < 1~,~2< x$$$${\small (2)}~x≦ -4~,~-2< x ≦-1$$$${\small (3)}~x< 1~,~2≦ x$$

p.13 練習6\({\small (1)}~\)定義域 \(x≧0\)、値域 \(y≧0\)

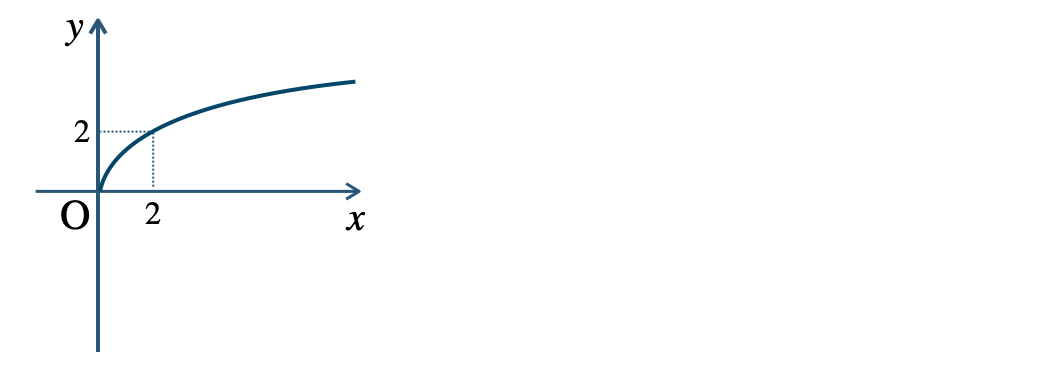
\({\small (2)}~\)定義域 \(x≧0\)、値域 \(y≦0\)

\({\small (3)}~\)定義域 \(x≦0\)、値域 \(y≧0\)

p.14 練習7\({\small (1)}~\)定義域 \(x≧1\)、値域 \(y≧0\)

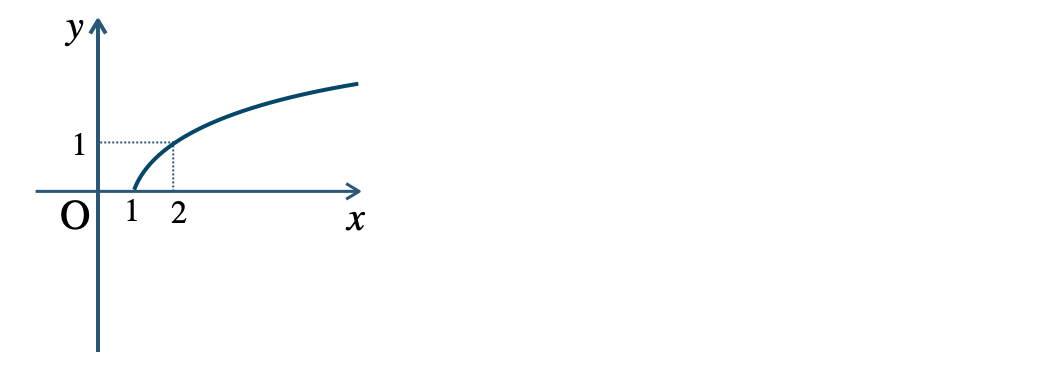
\({\small (2)}~\)定義域 \(x≦2\)、値域 \(y≧0\)

\({\small (3)}~\)定義域 \(x≧-1\)、値域 \(y≦0\)

p.15 練習8$${\small (1)}~(7~,~4)$$$${\small (2)}~(0~,~-1)$$

p.15 練習9$${\small (1)}~x≧2$$$${\small (2)}~-2≦x < -1$$

p.17 練習10$${\small (1)}~y=\frac{\,1\,}{\,3\,}x+\frac{\,1\,}{\,3\,}~~~(-1≦x≦5)$$$${\small (2)}~y=x^2~~~(x≦0)$$

p.17 練習11$${\small (1)}~y=\log_{3}x$$$${\small (2)}~y=4^x$$

p.18 練習12$${\small (1)}~y=\frac{\,x+3\,}{\,x-2\,}$$$${\small (2)}~y=\frac{\,-3x+2\,}{\,x+1\,}$$

p.18 練習13$${\small (1)}~y=\sqrt{x-2}$$$${\small (2)}~y=-\sqrt{-x}$$

p.19 練習14$$~~~a=\frac{\,1\,}{\,2\,}~,~b=3$$

p.19 練習15$${\small (1)}~y=-x^2~~(x≧0)$$

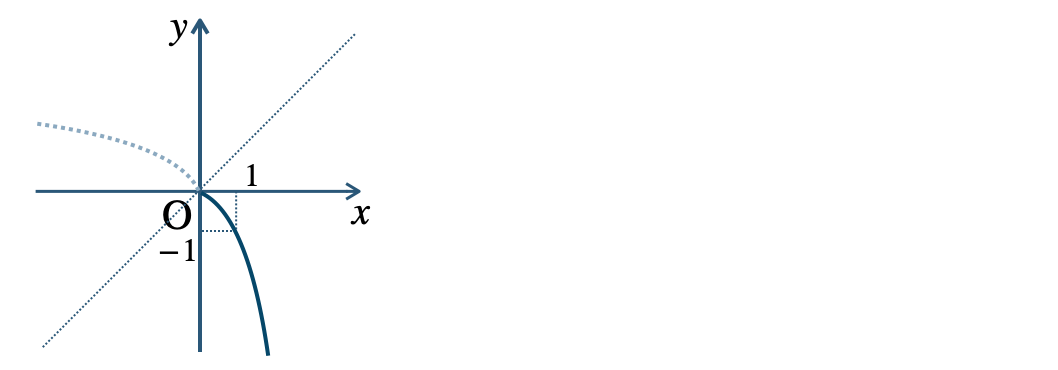
$${\small (2)}~y=\left(\frac{\,1\,}{\,2\,}\right)^x$$

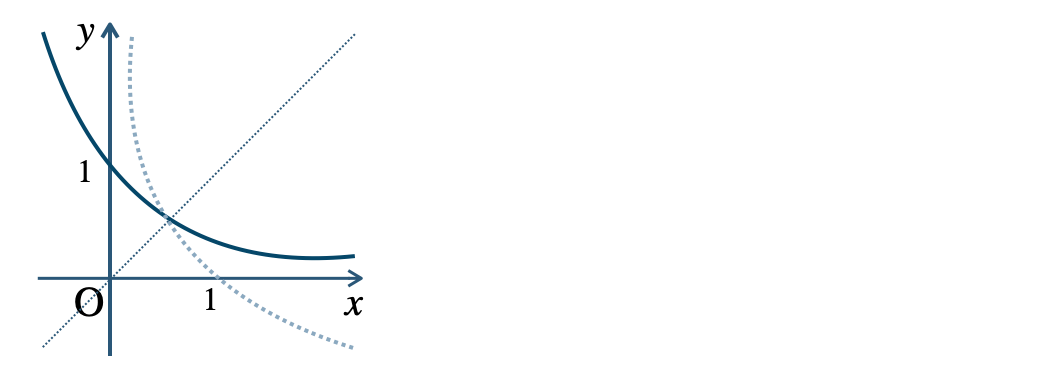
p.21 練習16$${\small (1)}~(g\circ f)(x)=\log_{2}(x^2+1)$$$${\small (2)}~(f\circ g)(x)=\{\log_{2}(x+1)\}^2$$

p.21 練習17$$\begin{eqnarray}~~~(f\circ g)(x)&=&f(g(x))
\\[2pt]~~~&=&\sqrt{x^2}
\\[2pt]~~~&=&x~~~(x≧0)
\end{eqnarray}$$また、$$\begin{eqnarray}~~~(g\circ f)(x)&=&g(f(x))
\\[2pt]~~~&=&\left(\sqrt{x}\right)^2
\\[2pt]~~~&=&x
\end{eqnarray}$$