1章 ベクトル

文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学C 1章 ベクトル
Advanced数学C 2章 平面上の曲線
Advanced数学C 3章 複素数平面
1章 ベクトル
1節 平面上のベクトル
互いに逆ベクトル \(\overrightarrow{b}\) と \(\overrightarrow{e}\)
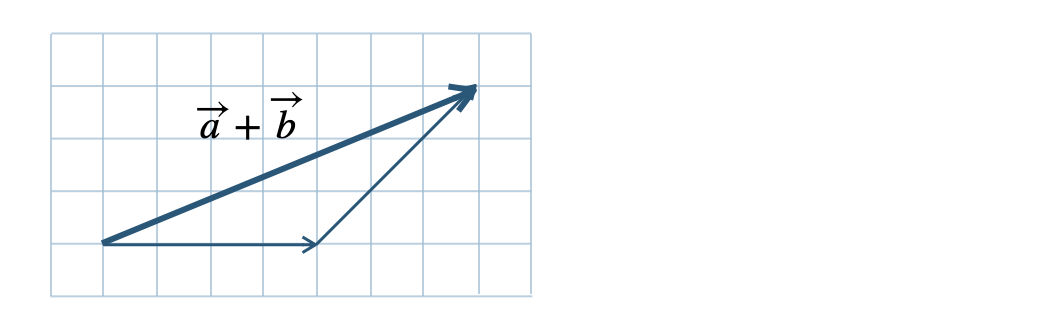
\({\small (2)}~\)
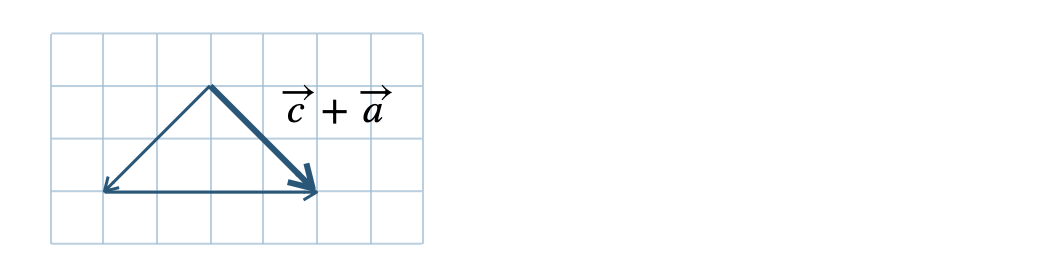
\({\small (3)}~\)
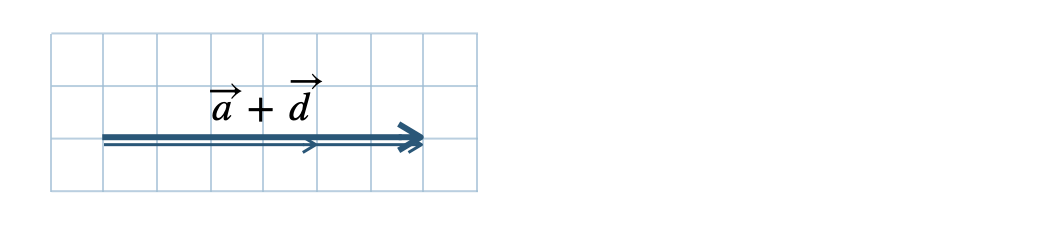
\({\small (4)}~\)

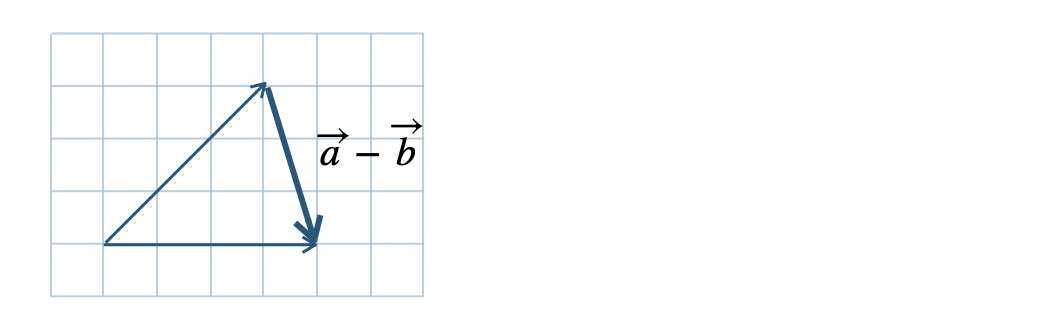
\({\small (2)}~\)
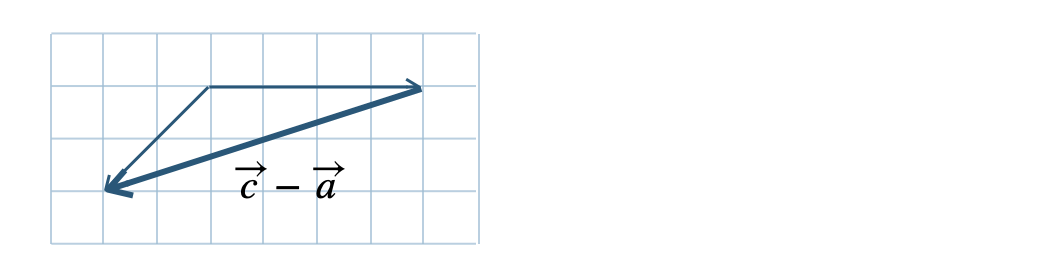
\({\small (3)}~\)

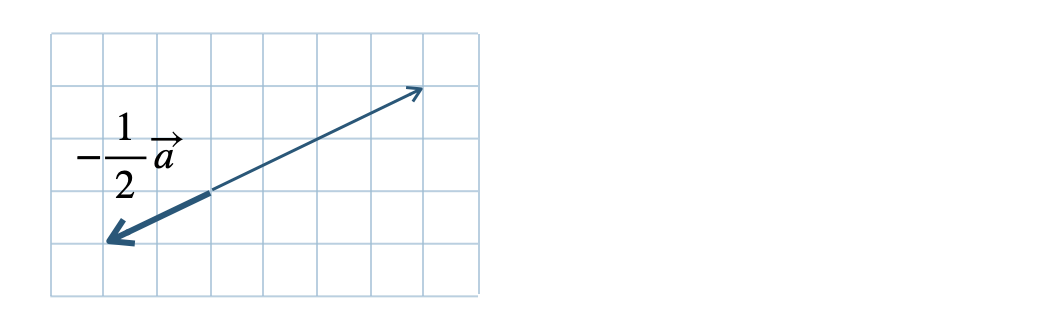
\({\small (2)}~\)
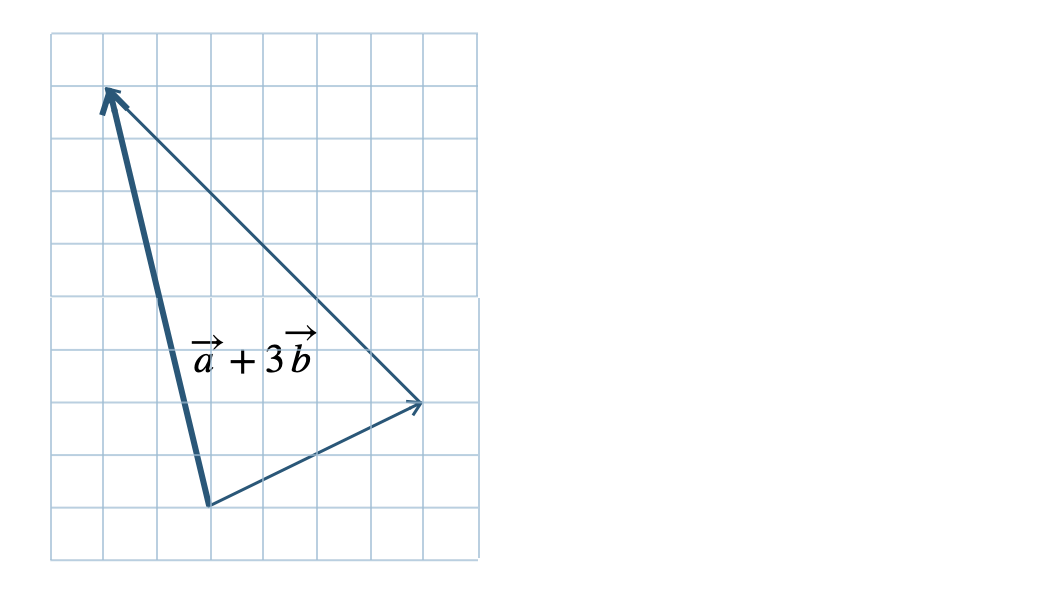
\({\small (3)}~\)
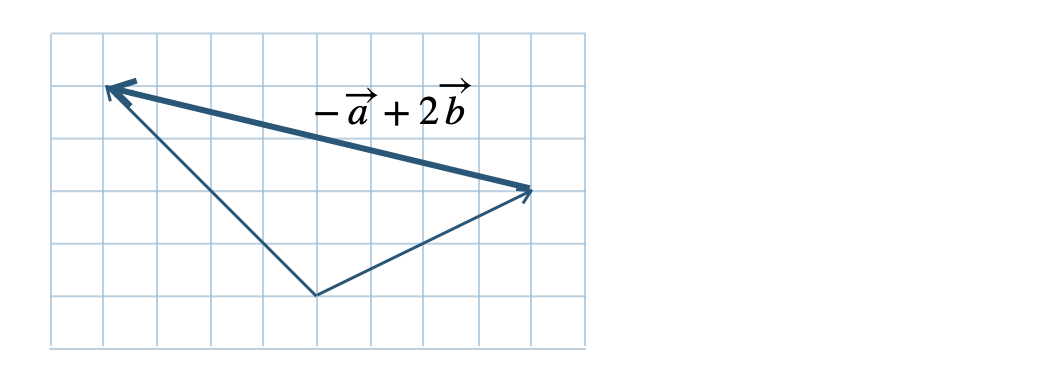
\({\small (4)}~\)
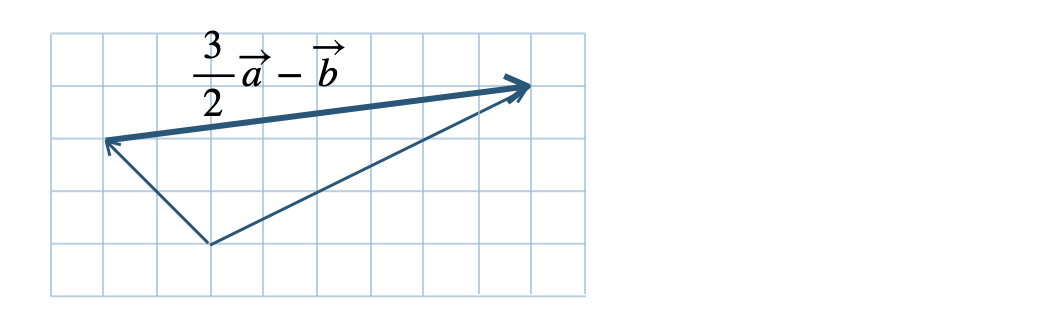
よって、$$~~~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{0^\circ}=|\overrightarrow{a}||\overrightarrow{b}|$$また、$$~~~\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\cos{180^\circ}=-|\overrightarrow{a}||\overrightarrow{b}|$$したがって、\(\overrightarrow{a}\,//\,\overrightarrow{b}\) ならば
\(\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|\) または \(\overrightarrow{a}\cdot\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|\)
[終]
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)\) とすると、
\(k\overrightarrow{a}=(ka_1,ka_2)~,~k\overrightarrow{b}=(kb_1,kb_2)\)
よって、
\((k\overrightarrow{a})\cdot\overrightarrow{b}=ka_1b_1+ka_2b_2\)
また、
\(\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2\)
これより、
\(k(\overrightarrow{a}\cdot\overrightarrow{b})=k(a_1b_1+a_2b_2)\)
\(=ka_1b_1+ka_2b_2\)
また、
\(\overrightarrow{a}\cdot(k\overrightarrow{b})=a_1kb_1+a_2kb_2\)
\(=ka_1b_1+ka_2b_2\)
したがって、
\((k\overrightarrow{a})\cdot\overrightarrow{b}=k(\overrightarrow{a}\cdot\overrightarrow{b})=\overrightarrow{a}\cdot(k\overrightarrow{b})\)
[終]
[証明]
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)~,~\overrightarrow{c}=(c_1,c_2)\) とすると、
\(\overrightarrow{a}+\overrightarrow{b}=(a_1+b_1,a_2+b_2)\) より、$$\begin{split}&(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}\\[2pt]~~=~&(a_1+b_1)c_1+(a_2+b_2)c_2\\[2pt]~~=~&a_1c_1+b_1c_1+a_2c_2+b_2c_2\\[2pt]~~=~&(a_1c_1+a_2c_2)+(b_1c_1+b_2c_2)\\[2pt]~~=~&\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{b}\cdot\overrightarrow{c}\end{split}$$したがって、$$~~~(\overrightarrow{a}+\overrightarrow{b})\cdot\overrightarrow{c}=\overrightarrow{a}\cdot\overrightarrow{c}+\overrightarrow{b}\cdot\overrightarrow{c}$$[終]
\(\overrightarrow{a}=(a_1,a_2)~,~\overrightarrow{b}=(b_1,b_2)~,~\overrightarrow{c}=(c_1,c_2)\) とすると、
\(\overrightarrow{b}-\overrightarrow{c}=(b_1-c_1,b_2-c_2)\) より、$$\begin{split}&\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})\\[2pt]~~=~&a_1(b_1-c_1)+a_2(b_2-c_2)\\[2pt]~~=~&a_1b_1-a_1c_1+a_2b_2-a_2c_2\\[2pt]~~=~&(a_1b_1+a_2b_2)-(a_1c_1+a_2c_2)\\[2pt]~~=~&\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}\end{split}$$したがって、$$~~~\overrightarrow{a}\cdot(\overrightarrow{b}-\overrightarrow{c})=\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{a}\cdot\overrightarrow{c}$$[終]
(左辺)
\(=|\overrightarrow{a}+\overrightarrow{b}|^2\)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}+\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}+\overrightarrow{a}\cdot\overrightarrow{b}\)
\(+\overrightarrow{b}\cdot\overrightarrow{a}+\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\(|\overrightarrow{a}+\overrightarrow{b}|^2=|\overrightarrow{a}|^2+2\overrightarrow{a}\cdot\overrightarrow{b}+|\overrightarrow{b}|^2\) [終]
\({\small (2)}~\)
(左辺)
\(=(\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot(\overrightarrow{a}-\overrightarrow{b})+\overrightarrow{b}(\overrightarrow{a}-\overrightarrow{b})\)
\(=\overrightarrow{a}\cdot\overrightarrow{a}-\overrightarrow{a}\cdot\overrightarrow{b}+\overrightarrow{b}\cdot\overrightarrow{a}-\overrightarrow{b}\cdot\overrightarrow{b}\)
\(=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
\(=\) (右辺)
したがって、
\((\overrightarrow{a}+\overrightarrow{b})\cdot(\overrightarrow{a}-\overrightarrow{b})=|\overrightarrow{a}|^2-|\overrightarrow{b}|^2\)
[終]
問題
\({\small (2)}~\)[証明]$$\begin{split}&\overrightarrow{\rm PQ}\\[3pt]~~=~&\frac{\,m\,}{\,m+n\,}\overrightarrow{\rm AC}-\frac{\,m\,}{\,m+n\,}\overrightarrow{\rm AB}\\[3pt]~~=~&\frac{\,m\,}{\,m+n\,}(\overrightarrow{\rm AC}-\overrightarrow{\rm AB})\\[3pt]~~=~&\frac{\,m\,}{\,m+n\,}\overrightarrow{\rm BC}\end{split}$$これより、\(\overrightarrow{\rm PQ}\) が \(\overrightarrow{\rm BC}\) の実数倍で表されるので、
\(\overrightarrow{\rm PQ}\,//\,\overrightarrow{\rm BC}\) [終]
\(\angle{\rm BOC}=\theta\) とすると、$$\begin{split}&{\rm OA\times OD}\\[2pt]~~=~&|\overrightarrow{\rm OA}||\overrightarrow{\rm OD}|\\[2pt]~~=~&|\overrightarrow{\rm OA}||\overrightarrow{\rm OB}|\cos{\theta}\\[2pt]~~=~&|\overrightarrow{a}||\overrightarrow{b}|\cos{\theta}\end{split}$$また、$$\begin{split}&{\rm OB\times OC}\\[2pt]~~=~&|\overrightarrow{\rm OB}||\overrightarrow{\rm OC}|\\[2pt]~~=~&|\overrightarrow{\rm OB}||\overrightarrow{\rm OA}|\cos{\theta}\\[2pt]~~=~&|\overrightarrow{a}||\overrightarrow{b}|\cos{\theta}\end{split}$$したがって、\({\rm OA\times OD}={\rm OB\times OC}\) [終]
2節 ベクトルの応用
\(m> n\) のとき、$$~~~\overrightarrow{\rm AQ}=\frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}$$\(m<; n\) のとき、$$~~~\overrightarrow{\rm AQ}=\frac{\,m\,}{\,n-m\,}\overrightarrow{\rm BA}=\frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}$$よって、どちらの場合でも、$$\begin{eqnarray}~~~\overrightarrow{q}&=&\overrightarrow{\rm OA}+\overrightarrow{\rm AQ}\\[2pt]~~~&=&\overrightarrow{\rm OA}+=\frac{\,m\,}{\,m-n\,}\overrightarrow{\rm AB}\\[2pt]~~~&=&\overrightarrow{a}+=\frac{\,m\,}{\,m-n\,}(\overrightarrow{b}-\overrightarrow{a})\\[2pt]~~~&=&\frac{\,(m-n)\overrightarrow{a}+m\overrightarrow{b}-m\overrightarrow{a}\,}{\,m-n\,}\\[2pt]~~~&=&\frac{\,-n\overrightarrow{a}+m\overrightarrow{b}\,}{\,m-n\,}\end{eqnarray}$$[終]
重心の位置ベクトルを \(\overrightarrow{g}\) とすると、$$~~~\overrightarrow{g}=\frac{\,\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,3\,}$$これより、$$\begin{split}&\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}\\[2pt]~~=~&(\overrightarrow{a}-\overrightarrow{g})+(\overrightarrow{b}-\overrightarrow{g})+(\overrightarrow{c}-\overrightarrow{g})\\[2pt]~~=~&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-3\overrightarrow{g}\\[2pt]~~=~&\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}-(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})\\[2pt]~~=~&\overrightarrow{0}\end{split}$$したがって、$$~~~\overrightarrow{\rm GA}+\overrightarrow{\rm GB}+\overrightarrow{\rm GC}=\overrightarrow{0}$$[終]
\(\overrightarrow{\rm AC}=\overrightarrow{b}+\overrightarrow{d}\) となる
点 \({\rm E}\) は辺 \({\rm BC}\) を \(3:2\) に内分するので、$$\begin{eqnarray}~~~\overrightarrow{\rm AE}&=&\frac{\,2\overrightarrow{\rm AB}+3\overrightarrow{\rm AC}\,}{\,3+2\,}\\[2pt]~~~&=&\frac{\,2\overrightarrow{b}+3(\overrightarrow{b}+\overrightarrow{d})\,}{\,5\,}\\[2pt]~~~&=&\frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,5\,}\end{eqnarray}$$点 \({\rm F}\) は辺 \({\rm BD}\) を \(3:5\) に内分するので、$$\begin{eqnarray}~~~\overrightarrow{\rm AF}&=&\frac{\,5\overrightarrow{\rm AB}+3\overrightarrow{\rm AD}\,}{\,3+5\,}\\[2pt]~~~&=&\frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,8\,}\\[2pt]~~~&=&\frac{\,5\,}{\,8\,}\times\frac{\,5\overrightarrow{b}+3\overrightarrow{d}\,}{\,5\,}=\frac{\,5\,}{\,8\,}\overrightarrow{\rm AE}\end{eqnarray}$$したがって、3点 \({\rm A~,~E~,~F}\) は一直線上にある [終]
\({\small (2)}~\)\(k:k-1\) に外分する
\end{split}$$ここで、二等辺三角形より \(|\overrightarrow{a}|=|\overrightarrow{b}|\)
これより、\(|\overrightarrow{b}|^2-|\overrightarrow{a}|^2\) となるので、$$~~~\overrightarrow{\rm OM}\cdot\overrightarrow{\rm AB}=0$$\(\overrightarrow{\rm OM}\neq\overrightarrow{0}~,~\overrightarrow{\rm AB}\neq\overrightarrow{0}\) より、\({\rm OM\perp AB}\) [終]
\(\angle{\rm A}=90^\circ\) より、\(\overrightarrow{b}\cdot\overrightarrow{c}=0\)
また、\({\rm AB:AC}=2:3\) より、$$~~~|\overrightarrow{c}|=\frac{\,3\,}{\,2\,}|\overrightarrow{b}|$$
次に、点 \({\rm P}\) は線分 \({\rm BC}\) を \(4:3\) に内分するので、$$~~~\overrightarrow{\rm AP}=\frac{\,3\,}{\,7\,}\overrightarrow{b}+\frac{\,4\,}{\,7\,}\overrightarrow{c}$$
点 \({\rm Q}\) は線分 \({\rm AC}\) を \(1:2\) に内分するので、$$\begin{eqnarray}~~~\overrightarrow{\rm BQ}&=&\frac{\,2\,}{\,3\,}\overrightarrow{\rm BA}+\frac{\,1\,}{\,3\,}\overrightarrow{\rm BC}\\[2pt]~~~&=&-\frac{\,2\,}{\,3\,}\overrightarrow{b}+\frac{\,1\,}{\,3\,}(\overrightarrow{c}-\overrightarrow{b})\\[2pt]~~~&=&-\overrightarrow{b}+\frac{\,1\,}{\,3\,}\overrightarrow{c}\end{eqnarray}$$これより、$$\begin{split}&\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BQ}\\[2pt]~~=~&\left(\frac{\,3\,}{\,7\,}\overrightarrow{b}+\frac{\,4\,}{\,7\,}\overrightarrow{c}\right)\cdot\left(-\overrightarrow{b}+\frac{\,1\,}{\,3\,}\overrightarrow{c}\right)\\[2pt]~~=~&-\frac{\,3\,}{\,7\,}|\overrightarrow{b}|^2+\frac{\,1\,}{\,7\,}\overrightarrow{b}\cdot\overrightarrow{c}\\[2pt]~~~~&~~~~~~~~~~~~-\frac{\,4\,}{\,7\,}\overrightarrow{b}\cdot\overrightarrow{c}+\frac{\,4\,}{\,21\,}|\overrightarrow{c}|^2\end{split}$$ここで、\(|\overrightarrow{c}|^2={\large \frac{\,9\,}{\,4\,}}|\overrightarrow{b}|^2~,~\overrightarrow{b}\cdot\overrightarrow{c}=0\) より、$$\begin{split}&\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BQ}\\[2pt]~~=~&-\frac{\,3\,}{\,7\,}|\overrightarrow{b}|^2+\frac{\,4\,}{\,21\,}\cdot\frac{\,9\,}{\,4\,}|\overrightarrow{b}|^2\\[2pt]~~=~&0\end{split}$$したがって、\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BQ}=0\) より \({\rm AP\perp BQ}\) [終]
\(\overrightarrow{a}=(a_1~,~a_2)~,~\overrightarrow{b}=(b_1~,~b_2)\) とすると、$$~~~|\overrightarrow{a}|^2={a_1}^2+{a_2}^2$$$$~~~|\overrightarrow{b}|^2={b_1}^2+{b_2}^2$$$$~~~\overrightarrow{a}\cdot\overrightarrow{b}=a_1b_1+a_2b_2$$これより、
$$\begin{split}&|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2\\[2pt]~~=~&({a_1}^2+{a_2}^2)({b_1}^2+{b_2}^2)\\[2pt]&~~~~~~~~~~~-(a_1b_1+a_2b_2)^2\\[2pt]~~=~&(a_1b_2)^2-2a_1a_2b_1b_2+(a_2b_1)^2\\[2pt]~~=~&(a_1b_2-a_2b_1)^2\end{split}$$したがって、$$\begin{eqnarray}~~~S&=&\frac{\,1\,}{\,2\,}\sqrt{|\overrightarrow{a}|^2|\overrightarrow{b}|^2-(\overrightarrow{a}\cdot\overrightarrow{b})^2}\\[2pt]~~~&=&\frac{\,1\,}{\,2\,}\sqrt{(a_1b_2-a_2b_1)^2}\\[2pt]~~~&=&\frac{\,1\,}{\,2\,}|a_1b_2-a_2b_1|\end{eqnarray}$$[終]
\({\small (2)}~3\)
x=2+t \\y=-3+2t
\end{array}\right.\end{eqnarray}$$$${\small (2)}~\begin{eqnarray} \left\{\begin{array}{l}
x=4-3t \\y=2t
\end{array}\right.\end{eqnarray}$$
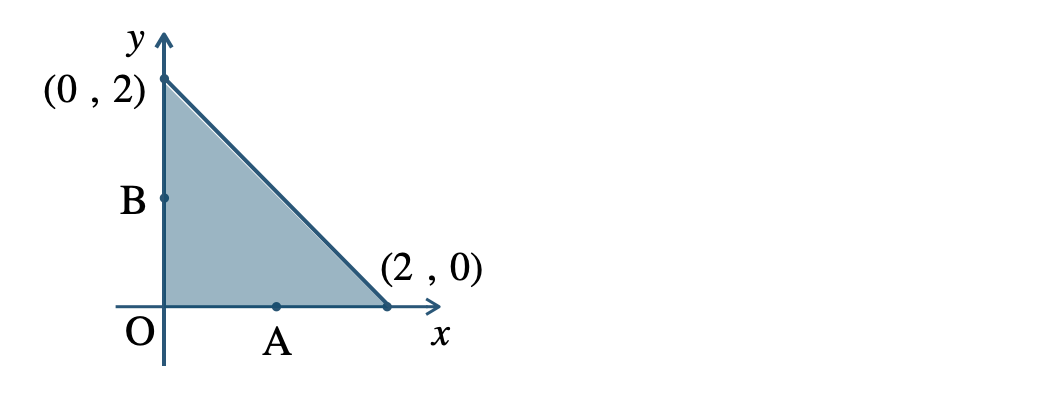
\({\small (2)}~\)中心 \({\large \frac{\,1\,}{\,3\,}}\overrightarrow{a}\)、半径 \(2\)
2点 \({\rm A}(\overrightarrow{a})~,~{\rm B}(\overrightarrow{b})\) を結ぶ線分 \({\rm AB}\) を直径とする円上の任意の点を \({\rm P}(\overrightarrow{p})\) とすると、
\(\angle{\rm APB}=90^\circ\) より、$$~~~\overrightarrow{\rm AP}\cdot\overrightarrow{\rm BP}=0$$したがって、$$~~~(\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{p}-\overrightarrow{b})=0$$[終]
(ⅰ) \({\rm A}\) と \({\rm P}\) が一致するとき、
\(\overrightarrow{\rm AP}=\overrightarrow{0}\)
よって、
\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)
(ⅱ) \({\rm A}\) と \({\rm P}\) が一致しないとき、
\(\overrightarrow{\rm AP}\perp\overrightarrow{\rm CA}\)
よって、
\(\overrightarrow{\rm AP}\cdot\overrightarrow{\rm CA}=0\)
これらより、いずれの場合でも
\((\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})=0\) …①
次に、\(|\overrightarrow{\rm CA}|=r\) より、
\(|\overrightarrow{a}-\overrightarrow{c}|^2=r^2\)
また、
\((\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\) …②
よって、①+②より
\((\overrightarrow{p}-\overrightarrow{a})\cdot(\overrightarrow{a}-\overrightarrow{c})\)
\(+(\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
\((\overrightarrow{p}-\overrightarrow{a}+\overrightarrow{a}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
\((\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\)
したがって、接線のベクトル方程式は、
\((\overrightarrow{p}-\overrightarrow{c})\cdot(\overrightarrow{a}-\overrightarrow{c})=r^2\) [終]
問題
$$\begin{eqnarray}~~~l\overrightarrow{\rm AP}+m\overrightarrow{\rm BP}+n\overrightarrow{\rm CP}&=&\overrightarrow{0}
\\[2pt]~~~l\overrightarrow{\rm AP}+m(\overrightarrow{\rm AP}-\overrightarrow{\rm AB})
\\[2pt]~~~+n(\overrightarrow{\rm AP}-\overrightarrow{\rm AC})&=&\overrightarrow{0}
\\[2pt]~~~~~~(l+m+n)\overrightarrow{\rm AP}&=&m\overrightarrow{\rm AB}+n\overrightarrow{\rm AC}\end{eqnarray}$$これより、$$\begin{eqnarray}~~~\overrightarrow{\rm AP}&=&\frac{\,m\overrightarrow{\rm AB}+n\overrightarrow{\rm AC}\,}{\,l+m+n\,}\\[3pt]~~~&=&\frac{\,m+n\,}{\,l+m+n\,}\times\frac{\,m\overrightarrow{\rm AB}+n\overrightarrow{\rm AC}\,}{\,n+m\,}\end{eqnarray}$$
ここで、$$~~~\overrightarrow{\rm AD}=\frac{\,m\overrightarrow{\rm AB}+n\overrightarrow{\rm AC}\,}{\,n+m\,}$$とすると、点 \({\rm D}\) は線分 \({\rm BC}\) を \(n:m\) に内分する点である
また、$$~~~\overrightarrow{\rm AP}=\frac{\,m+n\,}{\,l+m+n\,}\overrightarrow{\rm AD}$$ここで、\({\large \frac{\,m+n\,}{\,l+m+n\,}}< 1\)
これより、点 \({\rm P}\) は線分 \({\rm AD}\) 上にある
したがって、点 \({\rm P}\) は \(\triangle {\rm ABC}\) の内部にある [終]
また、2直線が垂直のとき、法線ベクトルも垂直となるので \(\overrightarrow{n_1}\cdot\overrightarrow{n_2}=0\) より、$$~~~a_1a_2+b_1b_2=0$$[終]
3節 空間におけるベクトル
\(y=3\) は \(zx\) 平面に平行で \(y\) 軸との交点の \(3\) の平面
\(z=-1\) は \(xy\) 平面に平行で \(z\) 軸との交点の \(-2\) の平面
\(|\overrightarrow{e_1}|=|\overrightarrow{e_2}|=|\overrightarrow{e_3}|=1\) より、$$~~~\overrightarrow{e_1}\cdot\overrightarrow{e_1}=1\times1\times\cos{0^\circ}=1$$同様に、$$~~~\overrightarrow{e_2}\cdot\overrightarrow{e_2}=1~,~\overrightarrow{e_3}\cdot\overrightarrow{e_3}=1$$したがって、$$~~~\overrightarrow{e_1}\cdot\overrightarrow{e_1}=\overrightarrow{e_2}\cdot\overrightarrow{e_2}=\overrightarrow{e_3}\cdot\overrightarrow{e_3}=1$$[終]
\({\small (2)}~\)[証明]
\(|\overrightarrow{e_1}|=|\overrightarrow{e_2}|=|\overrightarrow{e_3}|=1\) より、$$~~~\overrightarrow{e_1}\cdot\overrightarrow{e_2}=1\times1\times\cos{90^\circ}=0$$同様に、$$~~~\overrightarrow{e_2}\cdot\overrightarrow{e_3}=0~,~\overrightarrow{e_3}\cdot\overrightarrow{e_1}=0$$したがって、$$~~~\overrightarrow{e_1}\cdot\overrightarrow{e_2}=\overrightarrow{e_2}\cdot\overrightarrow{e_3}=\overrightarrow{e_3}\cdot\overrightarrow{e_1}=0$$[終]
\({\small (2)}~\) [証明] 点 \({\rm G’}\) は \(\triangle {\rm ABC}\) の重心より、$$~~~\overrightarrow{\rm OG’}=\frac{\,\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\,}{\,3\,}$$これより、$$\begin{eqnarray}~~~\overrightarrow{\rm OG’}&=&\frac{\,3\,}{\,2\,}\times\frac{\,2(\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c})\,}{\,9\,}\\[3pt]~~~&=&\frac{\,3\,}{\,2\,}\overrightarrow{\rm OG}\end{eqnarray}$$したがって、直線 \({\rm OG}\) は \(\triangle {\rm ABC}\) の重心 \({\rm G’}\) を通る [終]
問題
ここで、\(\overrightarrow{\rm AP}\) と \(\overrightarrow{n}\) の内積は、$$\begin{eqnarray}~~~\overrightarrow{\rm AP}\cdot\overrightarrow{n}&=&(l\overrightarrow{\rm AB}+m\overrightarrow{\rm AC})\cdot\overrightarrow{n}\\[2pt]~~~&=&l\overrightarrow{\rm AB}\cdot\overrightarrow{n}+m\overrightarrow{\rm AC}\cdot\overrightarrow{n}\end{eqnarray}$$ここで、\(\overrightarrow{\rm AB}\cdot\overrightarrow{n}=0~,~\overrightarrow{\rm AC}\cdot\overrightarrow{n}=0\) より、$$~~~\overrightarrow{\rm AP}\cdot\overrightarrow{n}=0$$したがって、\(\overrightarrow{\rm AP}\perp \overrightarrow{n}\) となる [終]
発展 平面の方程式
発展 空間における直線の方程式
次のページ「2章 平面上の曲線」


