このページは、東京書籍:Advanced数学C[701]
3章 複素数平面
3章 複素数平面

教科書の復習から入試の入門まで|数学入門問題精講
旺文社の入門問題精講シリーズの紹介高校生の皆さん、数学の勉強に困ったことはありませんか?教科書の内容...
リンク
文字数が多く、重くなるのでページを分割しています。
各章は下のリンクまたはページ下の「次へ」をクリックしてください。
Advanced数学C 1章 ベクトル
Advanced数学C 2章 平面上の曲線
Advanced数学C 3章 複素数平面
3章 複素数平面
1節 複素数平面
p.118 問1 点 \({\rm D}\) は、\(4-2i\)
点 \({\rm E}\) は、\(-3+4i\)
点 \({\rm F}\) は、\(-4\)
点 \({\rm E}\) は、\(-3+4i\)
点 \({\rm F}\) は、\(-4\)
p.118 問2

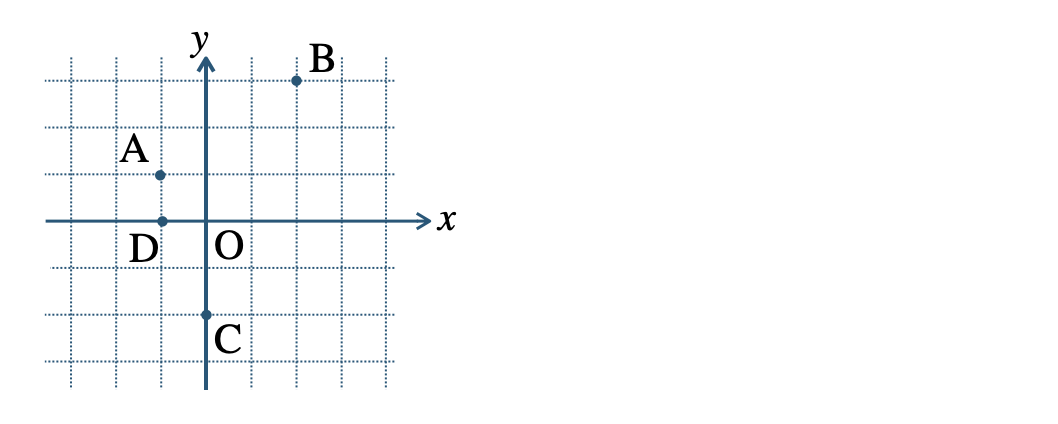
p.119 問3 実軸対称 \(2+3i\)
原点対称 \(-2+3i\)
虚軸対称 \(-2-3i\)
原点対称 \(-2+3i\)
虚軸対称 \(-2-3i\)
p.119 問4\({\small [1]}~\)[証明]$$\begin{split}&\overline {\alpha +\beta}
\\[2pt]~~=~&\overline {(a+bi)+(c+di)}
\\[2pt]~~=~&\overline {(a+c)+(b+d)i}
\\[2pt]~~=~&(a+c)-(b+d)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}+\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}+\overline {(c+di)}
\\[2pt]~~=~&(a-bi)+(c-di)
\\[2pt]~~=~&(a+c)-(b+d)i
\end{split}$$したがって、$$~~~\overline {\alpha +\beta}=\overline {\alpha}+\overline {\beta}$$[終]
\({\small [2]}~\)[証明]$$\begin{split}&\overline {\alpha -\beta}
\\[2pt]~~=~&\overline {(a+bi)-(c+di)}
\\[2pt]~~=~&\overline {(a-c)+(b-d)i}
\\[2pt]~~=~&(a-c)-(b-d)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}-\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}-\overline {(c+di)}
\\[2pt]~~=~&(a-bi)-(c-di)
\\[2pt]~~=~&(a-c)-(b-d)i
\end{split}$$したがって、$$~~~\overline {\alpha -\beta}=\overline {\alpha}-\overline {\beta}$$[終]
\({\small [3]}~\)[証明]$$\begin{split}&\overline {\alpha \beta}
\\[2pt]~~=~&\overline {(a+bi)(c+di)}
\\[2pt]~~=~&\overline {(ac-bd)+(ad+bc)i}
\\[2pt]~~=~&(ac-bd)-(ad+bc)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}\overline {(c+di)}
\\[2pt]~~=~&(a-bi)(c-di)
\\[2pt]~~=~&(ac-bd)-(ad+bc)i
\end{split}$$したがって、$$~~~\overline {\alpha \beta}=\overline {\alpha}\overline {\beta}$$[終]
\({\small [4]}~\)[証明]$$\begin{split}&\overline {\left( \frac{\,\alpha\,}{\,\beta\,} \right)}
\\[3pt]~~=~&\overline {\left( \frac{\,a+bi\,}{\,c+di\,} \right)}
\\[3pt]~~=~&\overline {\left\{ \frac{\,(ac+bd)+(bc-ad)i\,}{\,c^2+d^2\,} \right\}}
\\[3pt]~~=~&\frac{\,(ac+bd)-(bc-ad)i\,}{\,c^2+d^2\,}
\end{split}$$また、$$\begin{split}&\frac{\,\overline {\alpha}\,}{\,\overline {\beta}\,}
\\[3pt]~~=~&\frac{\,\overline {a+bi}\,}{\,\overline {c+di}\,}
\\[3pt]~~=~&\frac{\,a-bi\,}{\,c-di\,}
\\[2pt]~~=~&\frac{\,(ac+bd)-(bc-ad)i\,}{\,c^2+d^2\,}
\end{split}$$したがって、$$~~~\overline {\left( \frac{\,\alpha\,}{\,\beta\,} \right)}=\frac{\,\overline {\alpha}\,}{\,\overline {\beta}\,}$$[終]
\\[2pt]~~=~&\overline {(a+bi)+(c+di)}
\\[2pt]~~=~&\overline {(a+c)+(b+d)i}
\\[2pt]~~=~&(a+c)-(b+d)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}+\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}+\overline {(c+di)}
\\[2pt]~~=~&(a-bi)+(c-di)
\\[2pt]~~=~&(a+c)-(b+d)i
\end{split}$$したがって、$$~~~\overline {\alpha +\beta}=\overline {\alpha}+\overline {\beta}$$[終]
\({\small [2]}~\)[証明]$$\begin{split}&\overline {\alpha -\beta}
\\[2pt]~~=~&\overline {(a+bi)-(c+di)}
\\[2pt]~~=~&\overline {(a-c)+(b-d)i}
\\[2pt]~~=~&(a-c)-(b-d)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}-\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}-\overline {(c+di)}
\\[2pt]~~=~&(a-bi)-(c-di)
\\[2pt]~~=~&(a-c)-(b-d)i
\end{split}$$したがって、$$~~~\overline {\alpha -\beta}=\overline {\alpha}-\overline {\beta}$$[終]
\({\small [3]}~\)[証明]$$\begin{split}&\overline {\alpha \beta}
\\[2pt]~~=~&\overline {(a+bi)(c+di)}
\\[2pt]~~=~&\overline {(ac-bd)+(ad+bc)i}
\\[2pt]~~=~&(ac-bd)-(ad+bc)i
\end{split}$$また、$$\begin{split}&\overline {\alpha}\overline {\beta}
\\[2pt]~~=~&\overline {(a+bi)}\overline {(c+di)}
\\[2pt]~~=~&(a-bi)(c-di)
\\[2pt]~~=~&(ac-bd)-(ad+bc)i
\end{split}$$したがって、$$~~~\overline {\alpha \beta}=\overline {\alpha}\overline {\beta}$$[終]
\({\small [4]}~\)[証明]$$\begin{split}&\overline {\left( \frac{\,\alpha\,}{\,\beta\,} \right)}
\\[3pt]~~=~&\overline {\left( \frac{\,a+bi\,}{\,c+di\,} \right)}
\\[3pt]~~=~&\overline {\left\{ \frac{\,(ac+bd)+(bc-ad)i\,}{\,c^2+d^2\,} \right\}}
\\[3pt]~~=~&\frac{\,(ac+bd)-(bc-ad)i\,}{\,c^2+d^2\,}
\end{split}$$また、$$\begin{split}&\frac{\,\overline {\alpha}\,}{\,\overline {\beta}\,}
\\[3pt]~~=~&\frac{\,\overline {a+bi}\,}{\,\overline {c+di}\,}
\\[3pt]~~=~&\frac{\,a-bi\,}{\,c-di\,}
\\[2pt]~~=~&\frac{\,(ac+bd)-(bc-ad)i\,}{\,c^2+d^2\,}
\end{split}$$したがって、$$~~~\overline {\left( \frac{\,\alpha\,}{\,\beta\,} \right)}=\frac{\,\overline {\alpha}\,}{\,\overline {\beta}\,}$$[終]
p.121 問5$$~~~|-3+2i|=\sqrt{13}$$$$~~~|5+5i|=5\sqrt{2}$$$$~~~|-3i|=3$$
p.121 問6\(a~,~b\) を実数として、\(z=a+bi\) とすると、
\({\small [1]}~\)[証明]$$~~~|z|=\sqrt{a^2+b^2}$$$$\begin{eqnarray}~~~|-z|&=&|-a-bi|
\\[2pt]~~~&=&\sqrt{(-a)^2+(-b)^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$$$\begin{eqnarray}~~~|\overline {z}|&=&|a-bi|
\\[2pt]~~~&=&\sqrt{a^2+(-b)^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$したがって、$$~~~|z|=|-z|=|\overline {z}|$$[終]
\({\small [2]}~\)[証明]$$~~~|z|^2=a^2+b^2$$$$\begin{eqnarray}~~~z\overline {z}&=&(a+bi)(a-bi)
\\[2pt]~~~&=&a^2+b^2
\end{eqnarray}$$したがって、$$~~~|z|^2=z\overline {z}$$[終]
\({\small [1]}~\)[証明]$$~~~|z|=\sqrt{a^2+b^2}$$$$\begin{eqnarray}~~~|-z|&=&|-a-bi|
\\[2pt]~~~&=&\sqrt{(-a)^2+(-b)^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$$$\begin{eqnarray}~~~|\overline {z}|&=&|a-bi|
\\[2pt]~~~&=&\sqrt{a^2+(-b)^2}
\\[2pt]~~~&=&\sqrt{a^2+b^2}
\end{eqnarray}$$したがって、$$~~~|z|=|-z|=|\overline {z}|$$[終]
\({\small [2]}~\)[証明]$$~~~|z|^2=a^2+b^2$$$$\begin{eqnarray}~~~z\overline {z}&=&(a+bi)(a-bi)
\\[2pt]~~~&=&a^2+b^2
\end{eqnarray}$$したがって、$$~~~|z|^2=z\overline {z}$$[終]
p.121 問7$${\small (1)}~5$$$${\small (2)}~13$$
p.123 問8$${\small (1)}~\sqrt{2}\left( \cos{\frac{\,7\,}{\,4\,}\pi}+i\sin{\frac{\,7\,}{\,4\,}\pi} \right)$$$${\small (2)}~\sqrt{2}\left( \cos{\frac{\,5\,}{\,4\,}\pi}+i\sin{\frac{\,5\,}{\,4\,}\pi} \right)$$$${\small (3)}~2\left( \cos{\pi}+i\sin{\pi} \right)$$$${\small (4)}~\cos{\frac{\,11\,}{\,6\,}\pi}+i\sin{\frac{\,11\,}{\,6\,}\pi}$$$${\small (5)}~2\sqrt{3}\left( \cos{\frac{\,\pi\,}{\,6\,}}+i\sin{\frac{\,\pi\,}{\,6\,}} \right)$$$${\small (6)}~2\left( \cos{\frac{\,3\,}{\,2\,}\pi}+i\sin{\frac{\,3\,}{\,2\,}\pi} \right)$$
p.123 問9$$~~~|-z|=r~,~arg(-z)=\theta+\pi$$$$~~~|\overline {-z}|=r~,~arg(-\overline {z})=\pi-\theta$$
p.124 問10[証明]$$\small \begin{split}&\frac{\,z_1\,}{\,z_2\,}
\\[3pt]~~=~&\frac{\,r_1(\cos{\theta_1}+i\sin{\theta_1})\,}{\,r_2(\cos{\theta_2}+i\sin{\theta_2})\,}
\\[3pt]~~=~&\frac{\,r_1\,}{\,r_2\,}\cdot\frac{\,(\cos{\theta_1}+i\sin{\theta_1})(\cos{\theta_2}-i\sin{\theta_2})\,}{\,(\cos{\theta_2}+i\sin{\theta_2})(\cos{\theta_2}-i\sin{\theta_2})\,}\end{split}$$ここで、分子は、$$\begin{split}&(\cos{\theta_1}+i\sin{\theta_1})(\cos{\theta_2}-i\sin{\theta_2})
\\[2pt]~~=~&(\cos{\theta_1}\cos{\theta_2}+\sin{\theta_1}\sin{\theta_2})
\\[2pt]~~~&~~~~~~+i(\sin{\theta_1}\cos{\theta_2}-\cos{\theta_1}\sin{\theta_2})
\\[2pt]~~=~&\cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)}
\end{split}$$また、分母は、$$\begin{split}&(\cos{\theta_2}+i\sin{\theta_2})(\cos{\theta_2}-i\sin{\theta_2})
\\[2pt]~~=~&\cos^2{\theta_2}+\sin^2{\theta_2}
\\[2pt]~~=~&1
\end{split}$$よって、$$\small ~~~\frac{\,z_1\,}{\,z_2\,}=\frac{\,r_1\,}{\,r_2\,}\left\{ \cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)} \right\}$$したがって、$$~~~\left| \frac{\,z_1\,}{\,z_2\,} \right|=\frac{\,r_1\,}{\,r_2\,}=\frac{\,|z_1|\,}{\,|z_2|\,}$$$$~~~arg\left( \frac{\,z_1\,}{\,z_2\,} \right)=\theta_1-\theta_2=arg\,z_1-arg\, z_2$$[終]
\\[3pt]~~=~&\frac{\,r_1(\cos{\theta_1}+i\sin{\theta_1})\,}{\,r_2(\cos{\theta_2}+i\sin{\theta_2})\,}
\\[3pt]~~=~&\frac{\,r_1\,}{\,r_2\,}\cdot\frac{\,(\cos{\theta_1}+i\sin{\theta_1})(\cos{\theta_2}-i\sin{\theta_2})\,}{\,(\cos{\theta_2}+i\sin{\theta_2})(\cos{\theta_2}-i\sin{\theta_2})\,}\end{split}$$ここで、分子は、$$\begin{split}&(\cos{\theta_1}+i\sin{\theta_1})(\cos{\theta_2}-i\sin{\theta_2})
\\[2pt]~~=~&(\cos{\theta_1}\cos{\theta_2}+\sin{\theta_1}\sin{\theta_2})
\\[2pt]~~~&~~~~~~+i(\sin{\theta_1}\cos{\theta_2}-\cos{\theta_1}\sin{\theta_2})
\\[2pt]~~=~&\cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)}
\end{split}$$また、分母は、$$\begin{split}&(\cos{\theta_2}+i\sin{\theta_2})(\cos{\theta_2}-i\sin{\theta_2})
\\[2pt]~~=~&\cos^2{\theta_2}+\sin^2{\theta_2}
\\[2pt]~~=~&1
\end{split}$$よって、$$\small ~~~\frac{\,z_1\,}{\,z_2\,}=\frac{\,r_1\,}{\,r_2\,}\left\{ \cos{(\theta_1-\theta_2)}+i\sin{(\theta_1-\theta_2)} \right\}$$したがって、$$~~~\left| \frac{\,z_1\,}{\,z_2\,} \right|=\frac{\,r_1\,}{\,r_2\,}=\frac{\,|z_1|\,}{\,|z_2|\,}$$$$~~~arg\left( \frac{\,z_1\,}{\,z_2\,} \right)=\theta_1-\theta_2=arg\,z_1-arg\, z_2$$[終]
p.124 問11[証明]$$\begin{split}&\frac{\,1\,}{\,z\,}
\\[3pt]~~=~&\frac{\,\cos{0}+i\sin{0}\,}{\,r(\cos{\theta}+i\sin{\theta})\,}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}\left\{ \cos{(0-\theta)}+i\sin{(0-\theta)} \right\}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}\left\{ \cos{(-\theta)}+i\sin{(-\theta)} \right\}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}(\cos{\theta}-i\sin{\theta})
\end{split}$$[終]
\\[3pt]~~=~&\frac{\,\cos{0}+i\sin{0}\,}{\,r(\cos{\theta}+i\sin{\theta})\,}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}\left\{ \cos{(0-\theta)}+i\sin{(0-\theta)} \right\}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}\left\{ \cos{(-\theta)}+i\sin{(-\theta)} \right\}
\\[3pt]~~=~&\frac{\,1\,}{\,r\,}(\cos{\theta}-i\sin{\theta})
\end{split}$$[終]
p.125 問12$$~~~z_1z_2=-6$$$$~~~\frac{\,z_1\,}{\,z_2\,}=\frac{\,1\,}{\,3\,}-\frac{\,\sqrt{3}\,}{\,3\,}i$$
p.126 問13\({\small (1)}~\)点 \(z\) を原点 \({\rm O}\) を中心に \({\Large \frac{\,\pi\,}{\,3\,}}\) だけ回転し、原点からの距離を \(2\sqrt{3}\) 倍した点
\({\small (2)}~\)点 \(z\) を原点 \({\rm O}\) を中心に \({\Large \frac{\,3\,}{\,4\,}}\pi\) だけ回転し、原点からの距離を \(2\) 倍した点
\({\small (2)}~\)点 \(z\) を原点 \({\rm O}\) を中心に \({\Large \frac{\,3\,}{\,4\,}}\pi\) だけ回転し、原点からの距離を \(2\) 倍した点
p.127 問14$$~~~\left( \frac{\,1\,}{\,2\,}+\frac{\,\sqrt{3}\,}{\,2\,}i \right)z$$$$~~~\left( -\frac{\,\sqrt{2}\,}{\,2\,}+\frac{\,\sqrt{2}\,}{\,2\,}i \right)z$$$$~~~\left( -\frac{\,\sqrt{3}\,}{\,2\,}+\frac{\,1\,}{\,2\,}i \right)z$$$$~~~-iz$$
p.127 問15$$~~~\beta=-3+2i~,~3-2i$$
p.129 問16$${\small (1)}~1$$$${\small (2)}~i$$$${\small (3)}~-1$$
p.129 問17$${\small (1)}~-512i$$$${\small (2)}~-\frac{\,1\,}{\,4\,}$$$${\small (3)}~-1024-1024\sqrt{3}i$$
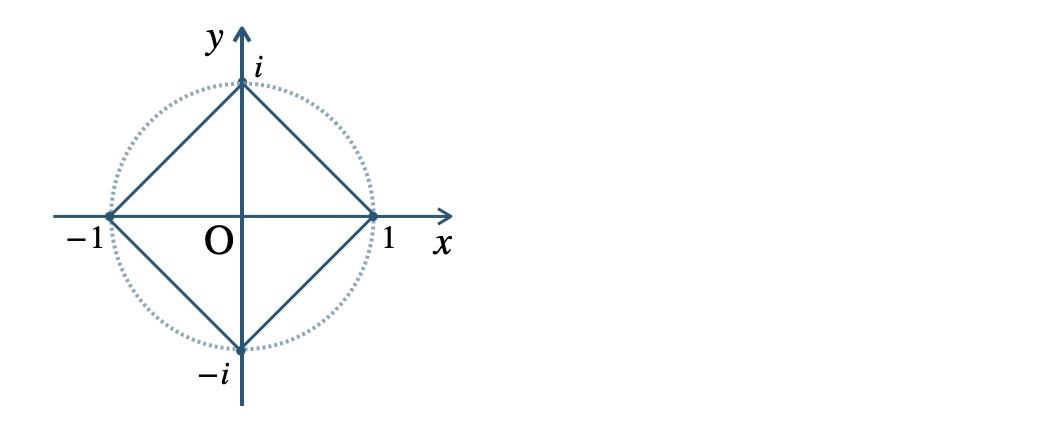
p.131 問18$${\small (1)}~1~,~i~,~-1~,~-i$$


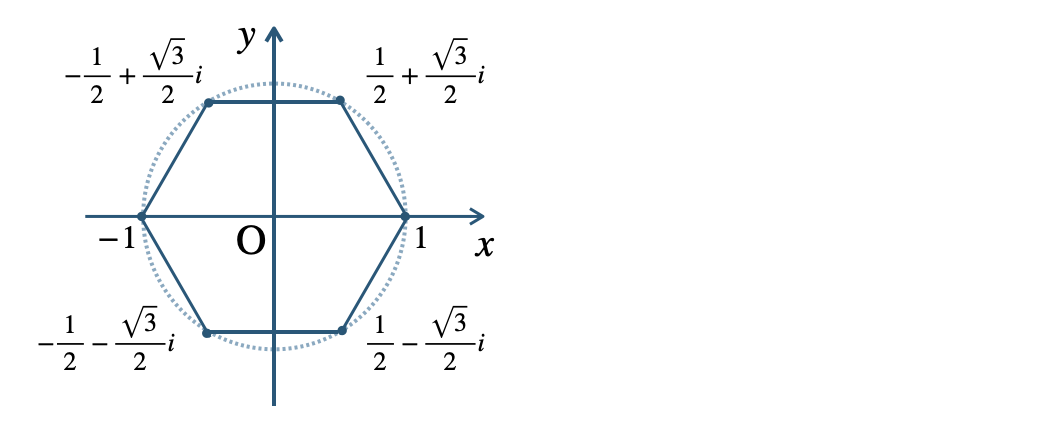
$${\small (2)}~1~,~\frac{\,1\,}{\,2\,}+\frac{\,\sqrt{3}\,}{\,2\,}i~,~-\frac{\,1\,}{\,2\,}+\frac{\,\sqrt{3}\,}{\,2\,}i$$$$~~~-1~,~-\frac{\,1\,}{\,2\,}-\frac{\,\sqrt{3}\,}{\,2\,}i~,~\frac{\,1\,}{\,2\,}-\frac{\,\sqrt{3}\,}{\,2\,}i$$
p.132 問19$${\small (1)}~z=-\frac{\,\sqrt{2}\,}{\,2\,}+\frac{\,\sqrt{6}\,}{\,2\,}i~,~\frac{\,\sqrt{2}\,}{\,2\,}-\frac{\,\sqrt{6}\,}{\,2\,}i$$$${\small (2)}~z=\sqrt{2}~,~1+i~,~\sqrt{2}i~,~-1+i$$$$~~~~,~-\sqrt{2}~,~-1-i~,~-\sqrt{2}i~,~1-i$$
2節 図形への応用
p.135 問1$${\small (1)}~5+i~,~17-11i$$$${\small (2)}~\frac{\,2+7i\,}{\,5\,}~,~-14+11i$$
p.135 問2$$~~~5+6i$$
p.136 問3\({\small (1)}~\)点 \(2i\) が中心、半径 \(3\) の円
\({\small (2)}~\)点 \(2-3i\) が中心、半径 \(4\) の円
\({\small (2)}~\)点 \(2-3i\) が中心、半径 \(4\) の円
p.136 問42点 \({\rm A}(3)~,~{\rm B}(-1+i)\) を結ぶ線分 \({\rm AB}\) の垂直二等分線
p.137 問6点 \({\Large \frac{\,5\,}{\,2\,}}i\) が中心、半径 \({\Large \frac{\,3\,}{\,2\,}}\) の円
p.138 問6\({\small (1)}~\)点 \(-1\) が中心、半径 \(1\) の円
\({\small (2)}~\)点 \(i\) が中心、半径 \(2\) の円
\({\small (2)}~\)点 \(i\) が中心、半径 \(2\) の円
p.139 問7$$~~~z=-2+5i$$
p.140 問8$$~~~\frac{\,2\,}{\,3\,}\pi$$
p.141 問9$$~~~\frac{\,2\,}{\,3\,}\pi$$
p.142 問10$${\small (1)}~x=9$$$${\small (2)}~x=4$$
p.143 問11\(\angle{\rm BAC}={\Large \frac{\,\pi\,}{\,2\,}}\) の直角二等辺三角形


