場合分けの必要な絶対値を含む方程式と不等式の解法
\(~~~|\,x-3\,|=2x+1\)
① 絶対値の中の正負で場合分けをする。
\({\small [\,1\,]}~x-3≧0\) すなわち \(x≧3\) のとき、
\(x-3=2x+1\)
\({\small [\,2\,]}~x-3<0\) すなわち \(x<3\) のとき、
\(-(x-3)=2x+1\)
② それぞれの場合の方程式の解を求める。
③ 求めた \(x\) の値が場合分けをした範囲を満たすか確認する。※ 満たさないときは解でない。
※ 不等式の場合は場合分けをした範囲と不等式の解の範囲の共通範囲が答えとなる。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
問題解説:場合分けの必要な絶対値を含む方程式と不等式
問題解説(1)
(ⅰ) \(x-2≧0\) のとき
\(x-2≧0\) より、\(x\) の範囲は \(x≧2\) となります。
絶対値をそのまま外せるので、$$~~~x-2=2x-7$$\(-2\) を左辺に、\(2x\) を右辺に移項すると、$$~x-2x=-7+2$$$$\hspace{18pt}-x=-5$$$$\hspace{26pt}x=5$$これは \(x≧2\) の範囲を満たす。よって、\(x=5\) となります。
(ⅱ) \(x-2<0\) のとき
\(x-2<0\) より、\(x\) の範囲は \(x<2\) となります。
絶対値はマイナスを付けて外すので、$$~~-(x-2)=2x-7$$$$~~~~~-x+2=2x-7$$\(2\) を左辺に、\(2x\) を右辺に移項すると、$$~-x-2x=-7-2$$$$\hspace{24pt}-3x=-9$$$$\hspace{37pt}x=3$$これは \(x<2\) の範囲を満たしません。よって、\(x=3\) は不適となります。
(ⅰ)と(ⅱ)より、答えは \(x=5\) となります。
問題解説(2)
(ⅰ) \(x-3≧0\) のとき
\(x-3≧0\) より、\(x\) の範囲は \(x≧3\) となります。
絶対値をそのまま外せるので、$$~~~~x-3≧5x+1$$\(-3\) を左辺に、\(5x\) を右辺に移項すると、$$~~x-5x≧1+3$$$$\hspace{17pt}-4x≧4$$\(-4\) で両辺をわり算すると、不等号の向きが逆になるので、$$\hspace{28pt}x≦-1$$これと、\(x≧3\) に共通範囲より、
共通範囲がないので不適となります。
(ⅱ) \(x-3<0\) のとき
\(x-3<0\) より、\(x\) の範囲は \(x<3\) となります。
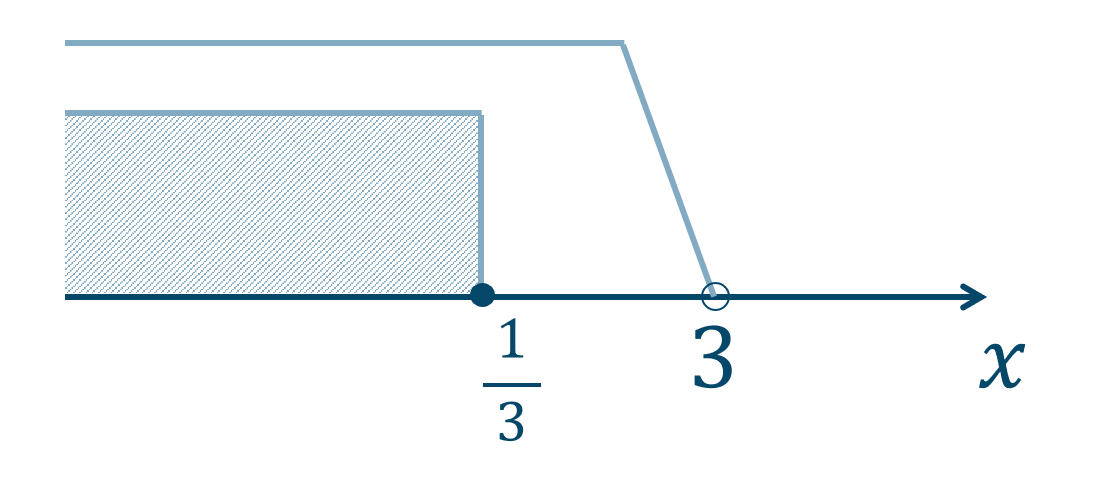
絶対値はマイナスを付けて外すので、$$~~~-(x-3)≧5x+1$$$$~~~~~-x+3≧5x+1$$\(3\) を左辺に、\(5x\) を右辺に移項すると、$$~~-x-5x≧1-3$$$$\hspace{27pt}-6x≧-2$$\(-6\) で両辺をわり算すると、不等号の向きが逆になるので、$$\hspace{40pt}x≦\frac{-2}{-6}$$$$\hspace{40pt}x≦\frac{1}{3}$$これと、\(x<3\) の共通範囲より
答えは \(x≦{\Large \frac{1}{3}}\) となります。
(ⅰ)と(ⅱ)より、答えは \(x≦{\Large \frac{1}{3}}\) となります。
今回のまとめ
難しいパターンの絶対値を含む式の解法を解説していきました。絶対値を場合分けを用いて解く方法は、方程式や不等式だけでなく様々な単元で用いますのでしっかりと覚えておきましょう。