今回の問題は「条件の真偽」です。
問題次の命題の真偽を答えよ。また、偽の場合は反例を1つあげよ。
\({\small (1)}~ab>0\) ならば \(a>0\) かつ \(b>0\)
\({\small (2)}~a=1\) かつ \(b=2\) ならば \(a+b=3\)
\({\small (3)}~x^2≧9\) ならば \(x≧3\)
\({\small (4)}~3≦x≦4\) ならば \(-1<x\)
\({\small (5)}~n\) が3の倍数ならば \(n\) は6の倍数である
\({\small (1)}~ab>0\) ならば \(a>0\) かつ \(b>0\)
\({\small (2)}~a=1\) かつ \(b=2\) ならば \(a+b=3\)
\({\small (3)}~x^2≧9\) ならば \(x≧3\)
\({\small (4)}~3≦x≦4\) ならば \(-1<x\)
\({\small (5)}~n\) が3の倍数ならば \(n\) は6の倍数である
Point:命題と条件の真偽■ 命題と条件正しいか正しくないかの判定ができる事柄を表す式や文を「命題」という。
正しいときは「真」である
正しくないときは「偽」である
(例) \(\sqrt{3}\) は無理数である→真
命題の中で変数 \(x\) を含み、その変数 \(x\) の値によって真偽が変わるものを「条件」という。
(例) \(x\) は無理数である
\(x=\sqrt{3}\) のとき→真、\(x=3\) のとき→偽
■ 仮定と結論
命題を2つの条件 \(p\) (仮定)と \(q\) (結論)を用いて、
\(p~\Rightarrow~q\) 「\(p\) ならば \(q\)」
すべての \(p\) が \(q\) も成り立つ
\({\small (2)}~\)\(p~\Rightarrow~q\) が偽のとき、
\(p\) を満たすが \(q\) を満たさないものがある
→ このときの例を「反例」という
正しいときは「真」である
正しくないときは「偽」である
(例) \(\sqrt{3}\) は無理数である→真
命題の中で変数 \(x\) を含み、その変数 \(x\) の値によって真偽が変わるものを「条件」という。
(例) \(x\) は無理数である
\(x=\sqrt{3}\) のとき→真、\(x=3\) のとき→偽
■ 仮定と結論
命題を2つの条件 \(p\) (仮定)と \(q\) (結論)を用いて、
\(p~\Rightarrow~q\) 「\(p\) ならば \(q\)」
\({\small (1)}~\)\(p~\Rightarrow~q\) が真のとき、
すべての \(p\) が \(q\) も成り立つ
\({\small (2)}~\)\(p~\Rightarrow~q\) が偽のとき、
\(p\) を満たすが \(q\) を満たさないものがある
→ このときの例を「反例」という
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
Point:集合を用いた命題の真偽
\({\rm P}\) が \({\rm Q}\) の部分集合 \({\rm P\subset Q}\) であれば真

命題「\(p~\Rightarrow~q\)」の真偽を判断するとき、
条件 \(p\) を満たす \(x\) の集合を \({\rm P}\)
条件 \(q\) を満たす \(x\) の集合を \({\rm Q}\)
とすると、
\({\rm P}\) が \({\rm Q}\) の部分集合 \({\rm P\subset Q}\) であれば真
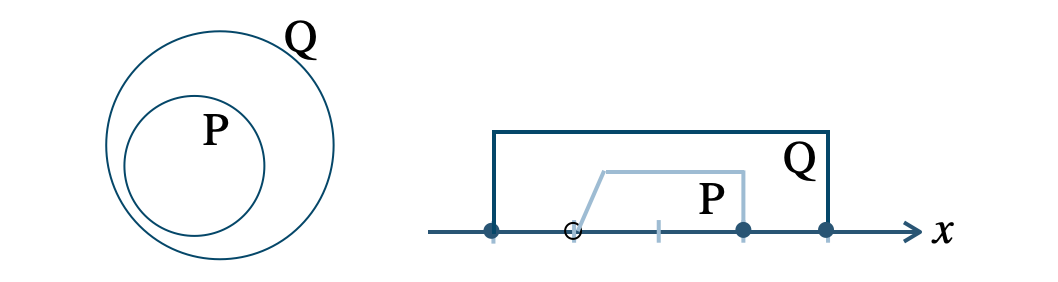
※ \({\rm Q}\) にならない \({\rm P}\) の要素 \(x\) な存在するならば、これが反例となり偽となる。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


