今回の問題は「条件の否定①(かつ・または)」です。
問題次の条件の否定を答えよ。ただし、文字はすべて実数とする。
\({\small (1)}~n\) は有理数である
\({\small (2)}~x=3\)
\({\small (3)}~-1≦x<2\)
\({\small (4)}~x>0\) かつ \(y≦0\)
\({\small (5)}~x≧0\) または \(y>-2\)
\({\small (1)}~n\) は有理数である
\({\small (2)}~x=3\)
\({\small (3)}~-1≦x<2\)
\({\small (4)}~x>0\) かつ \(y≦0\)
\({\small (5)}~x≧0\) または \(y>-2\)
Point:かつ・またはの否定■ 条件の否定
条件の否定は、その条件を集合としたときの補集合となる。
例えば、実数 \(x\) において、
条件 \(x=0\) の否定は、\(x\neq 0\)
条件 \(x≧1\) の否定は、\(x< 1\)
■ かつ・またはの否定
ド・モルガンの法則を用いて、
\({\small (1)}~\)2つの条件がともに成り立つの否定
\(p\) かつ \(q\) の否定は、\(\overline {\,p\,}\) または \(\overline {\,q\,}\)
\({\small (2)}~\)2つの条件の少なくとも一方が成り立つの否定
\(p\) または \(q\) の否定は、\(\overline {\,p\,}\) かつ \(\overline {\,q\,}\)
条件の否定は、その条件を集合としたときの補集合となる。
例えば、実数 \(x\) において、
条件 \(x=0\) の否定は、\(x\neq 0\)
条件 \(x≧1\) の否定は、\(x< 1\)
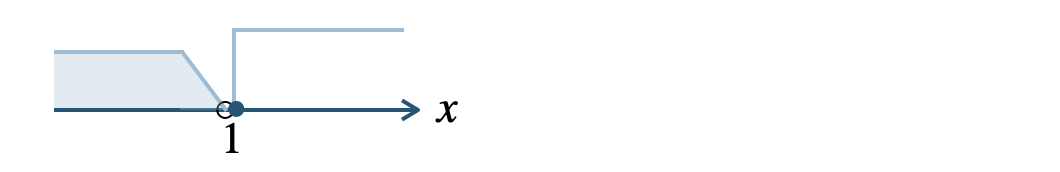
■ かつ・またはの否定
ド・モルガンの法則を用いて、
\({\small (1)}~\)2つの条件がともに成り立つの否定
\(p\) かつ \(q\) の否定は、\(\overline {\,p\,}\) または \(\overline {\,q\,}\)
\({\small (2)}~\)2つの条件の少なくとも一方が成り立つの否定
\(p\) または \(q\) の否定は、\(\overline {\,p\,}\) かつ \(\overline {\,q\,}\)
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


