今回の問題は「必要条件と十分条件」です。
問題次の \(p~,~q\) に対して、\(p\) は \(q\) の何になるか「必要条件である」、「十分条件である」、「必要十分条件である」、「必要条件でも十分条件でもない」の中から選んで答えよ。また、文字はすべて実数である。
\({\small (1)}~p\):\(x^2=4\)、\(q\):\(x=2\)
\({\small (2)}~p\):\(x~,~y\) がともに有理数、\(q\):\(xy\)が有理数
\({\small (3)}~p\):\(xy>0\)、\(q\):\(x>0\) かつ \(y>0\)
\({\small (4)}~p\):ある四角形がひし形、\(q\) :ある四角形が平行四辺形
\({\small (5)}~p\):2つの正方形が合同、\(q\):2つの正方形の面積が等しい
\({\small (1)}~p\):\(x^2=4\)、\(q\):\(x=2\)
\({\small (2)}~p\):\(x~,~y\) がともに有理数、\(q\):\(xy\)が有理数
\({\small (3)}~p\):\(xy>0\)、\(q\):\(x>0\) かつ \(y>0\)
\({\small (4)}~p\):ある四角形がひし形、\(q\) :ある四角形が平行四辺形
\({\small (5)}~p\):2つの正方形が合同、\(q\):2つの正方形の面積が等しい
Point:必要条件と十分条件の判別\(p\) は \(q\) であるための◯◯条件であるの判別は、
① 命題を矢印を用いて、\(p\,⇄\,q\) で表す。
② 行きと帰りのそれぞれの真偽を調べる。
\(p→q\) ( \(p\) ならば \(q\) )
\(p←q\) ( \(q\) ならば \(p\) )
③ 行き(十分条件)と帰り(必要条件)より、答え方を判別する。※ 真を○、偽を×とする。

\({\small [\,1\,]}~\)十分条件である。(必要条件ではない)
\({\small [\,2\,]}~\)必要条件である。(十分条件ではない)
\({\small [\,3\,]}~\)必要十分条件である。
※ このとき、互いに「同値」という。
\({\small [\,4\,]}~\)必要条件でも十分条件でもない。
① 命題を矢印を用いて、\(p\,⇄\,q\) で表す。
② 行きと帰りのそれぞれの真偽を調べる。
\(p→q\) ( \(p\) ならば \(q\) )
\(p←q\) ( \(q\) ならば \(p\) )
③ 行き(十分条件)と帰り(必要条件)より、答え方を判別する。※ 真を○、偽を×とする。
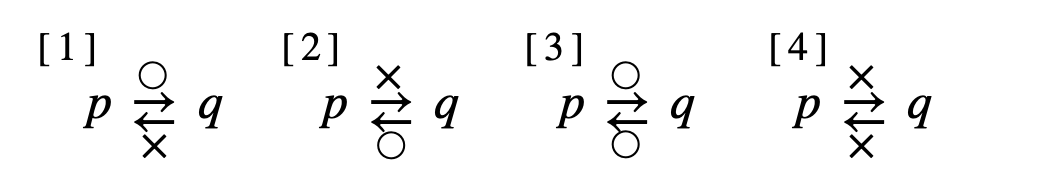
上の図より、\(p\) は \(q\) であるための、
\({\small [\,1\,]}~\)十分条件である。(必要条件ではない)
\({\small [\,2\,]}~\)必要条件である。(十分条件ではない)
\({\small [\,3\,]}~\)必要十分条件である。
※ このとき、互いに「同値」という。
\({\small [\,4\,]}~\)必要条件でも十分条件でもない。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


