今回の問題は「逆・裏・対偶」です。
問題次の命題の逆と裏と対偶を答えよ。また、それぞれの真偽も答えよ。
\(x=2\) かつ \(y=3\) ならば \(xy=6\)
\(x=2\) かつ \(y=3\) ならば \(xy=6\)
Point:逆・裏・対偶とその性質命題 \(p~\Rightarrow~q\) ( \(p\) ならば \(q\) ) に対して、
逆は、 \(q~\Rightarrow~p\) ( \(q\) ならば \(p\) )
裏は、 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) ( \(\overline {\,p\,}\) ならば \(\overline {\,q\,}\) )
対偶は、\(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\) ( \(\overline {\,q\,}\) ならば \(\overline {\,p\,}\) )

命題の真偽とその対偶の真偽は一致するので、
命題 \(p~\Rightarrow~q\) と 対偶 \(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\)
命題 \(q~\Rightarrow~p\) と 対偶 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\)
の真偽はそれぞれ一致する。
逆は、 \(q~\Rightarrow~p\) ( \(q\) ならば \(p\) )
裏は、 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) ( \(\overline {\,p\,}\) ならば \(\overline {\,q\,}\) )
対偶は、\(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\) ( \(\overline {\,q\,}\) ならば \(\overline {\,p\,}\) )
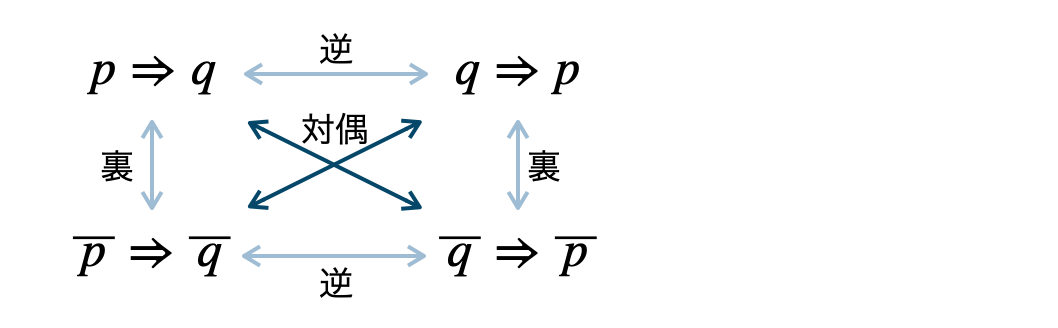
※ \(q~\Rightarrow~p\) と \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\) も対偶の関係
命題の真偽とその対偶の真偽は一致するので、
命題 \(p~\Rightarrow~q\) と 対偶 \(\overline {\,q\,}~\Rightarrow~\overline {\,p\,}\)
命題 \(q~\Rightarrow~p\) と 対偶 \(\overline {\,p\,}~\Rightarrow~\overline {\,q\,}\)
の真偽はそれぞれ一致する。
©︎ 2024 教科書より詳しい高校数学 yorikuwa.com
次のページ「解法のPointと問題解説」


