関数の値域と最大値・最小値の求め方
関数 \(y=f(x)\) について、変数 \(x\) の値の範囲を「定義域」といいます。
また、\(x\) がこの定義域全体を動くとき、\(f(x)\) の値の範囲を「値域」といいます。
関数 \(y=f(x)\) の定義域が \(a≦x≦b\) のとき、次のように表します。
・関数の最大値・最小値
関数の値域のなかで最大の値を「最大値」、最小の値を「最小値」といいます。
最大値と最小値は必ずグラフを描いて視覚的に判断しましょう。
問題解説:関数の値域と最大値・最小値
問題解説(1)
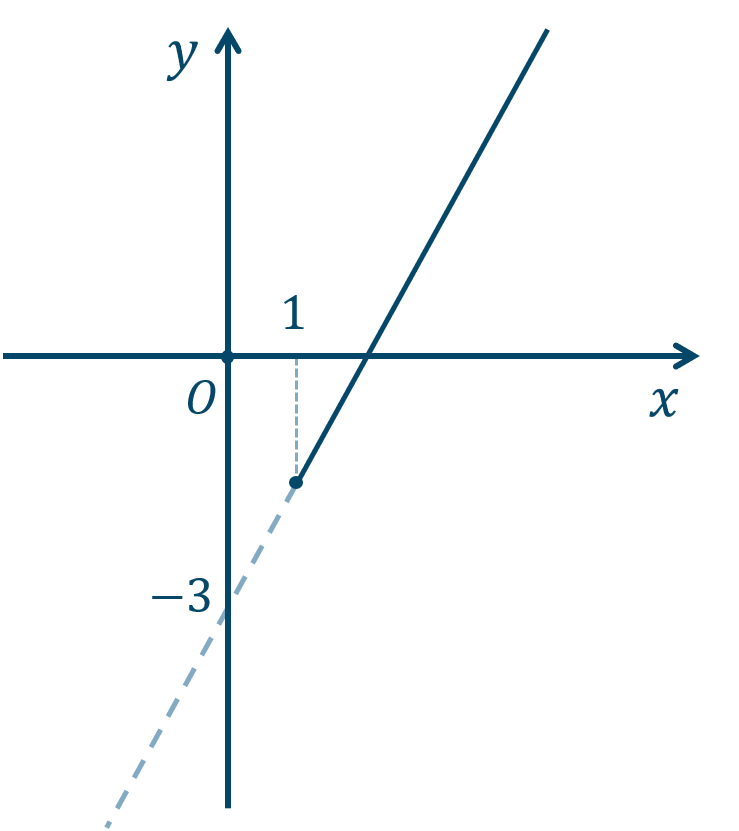
傾き \(2\)、\(y\) 切片が \(-3\) のグラフを描くと、
グラフより、\(x=1\) のとき、$$\hspace{ 10 pt}y=2\cdot 1-3$$$$\hspace{ 18 pt}=2-3$$$$\hspace{ 18 pt}=-1$$これより、値域は \(-1≦y\) となります。
また、最大値はなし、
最小値は \(-1\) で \(x=1\) のときとなります。
問題解説(2)
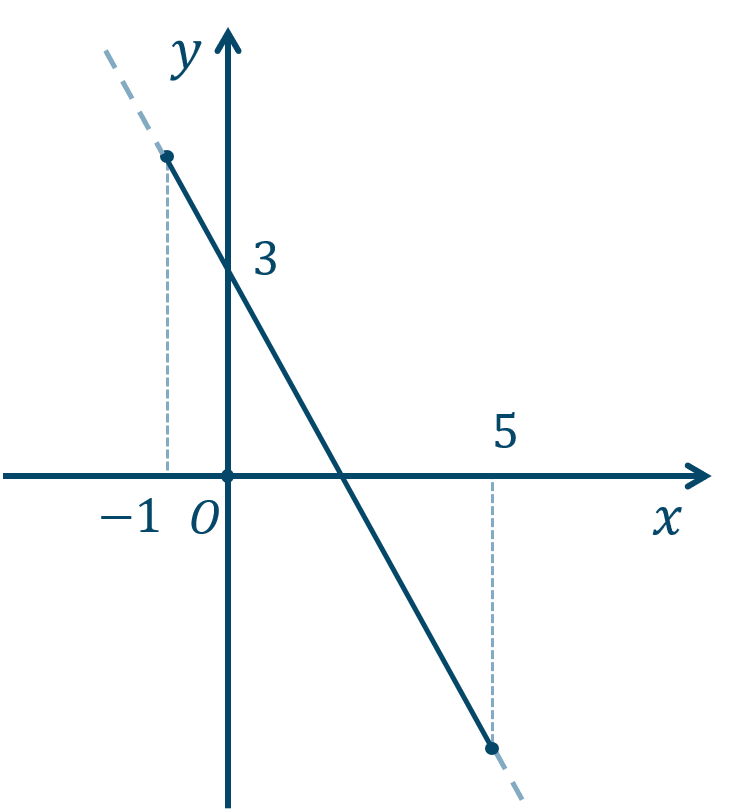
傾き \(-2\)、\(y\) 切片が \(3\) のグラフを描くと、
グラフより、\(x=-1\) のとき、$$\hspace{ 10 pt}y=-2\cdot (-1)+3$$$$\hspace{ 18 pt}=2+3$$$$\hspace{ 18 pt}=5$$また、\(x=5\) のとき、$$\hspace{ 10 pt}y=-2 \cdot 5+3$$$$\hspace{ 18 pt}=-10+3$$$$\hspace{ 18 pt}=-7$$よって、値域は \(-7≦y≦5\) となります。
また、最大値は \(5\) で \(x=-1\) のときとなり、
最小値は \(-7\) で \(x=5\) のときとなります。
問題解説(3)
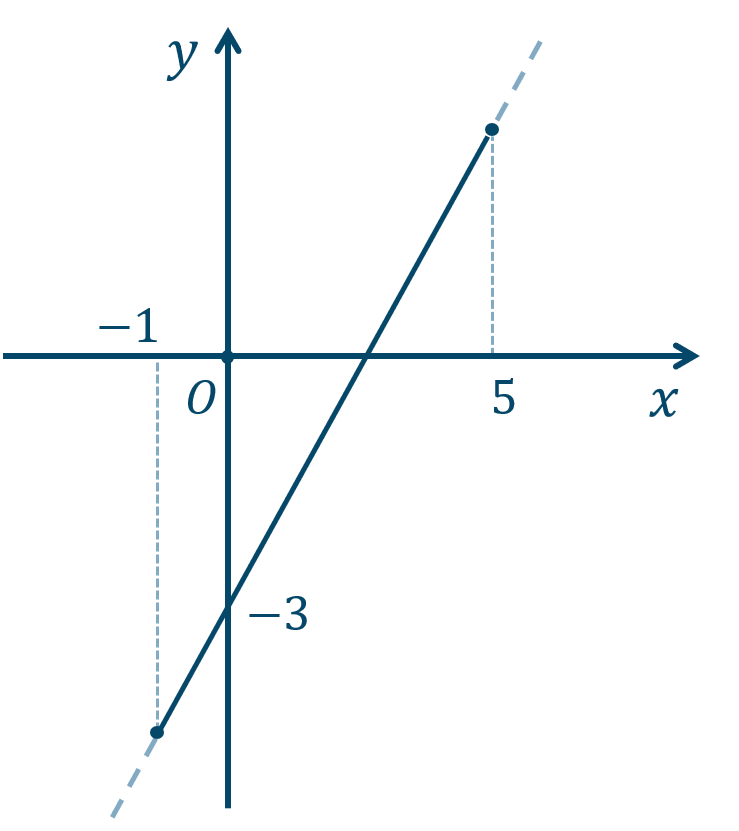
傾き \(2\)、\(y\) 切片が \(-3\) のグラフを描くと、
グラフより、\(x=-1\) のとき、$$\hspace{ 10 pt}y=2\cdot (-1)-3$$$$\hspace{ 18 pt}=-2-3$$$$\hspace{ 18 pt}=-5$$また、\(x=5\) のとき、$$\hspace{ 10 pt}y=2\cdot 5-3$$$$\hspace{ 18 pt}=10-3$$$$\hspace{ 18 pt}=7$$よって、値域は \(-5≦y≦7\) となります。
また、最大値は \(7\) で \(x=5\) のときとなり、
最小値は \(-5\) で \(x=-1\) のときとなります。
問題解説(4)
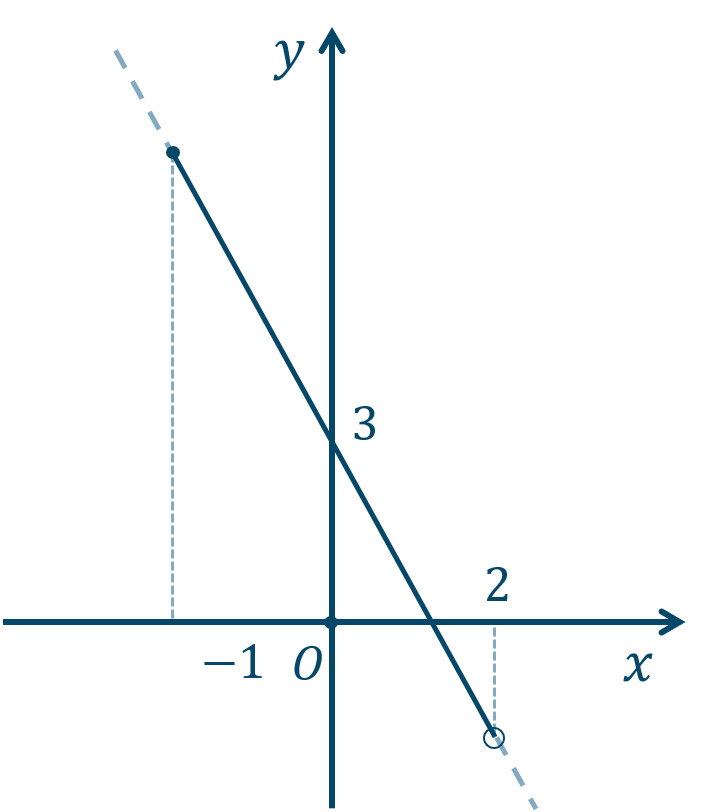
傾き \(-2\)、\(y\) 切片が \(3\) のグラフを描くと、
グラフより、\(x=-3\) のとき、$$\hspace{ 10 pt}y=-2\cdot (-3)+3$$$$\hspace{ 18 pt}=6+3$$$$\hspace{ 18 pt}=9$$また、\(x=2\) のとき、$$\hspace{ 10 pt}y=-2\cdot 2+3$$$$\hspace{ 18 pt}=-4+3$$$$\hspace{ 18 pt}=-1$$よって、値域は \(-1<y≦9\) となります。
また、最大値は \(9\) で \(x=-3\) のときとなり、
最小値はなしとなります。
今回のまとめ
定義域より、値域や最大値・最小値を求めるときは、グラフを描いて視覚的にどのようになるかを確認して求めましょう。