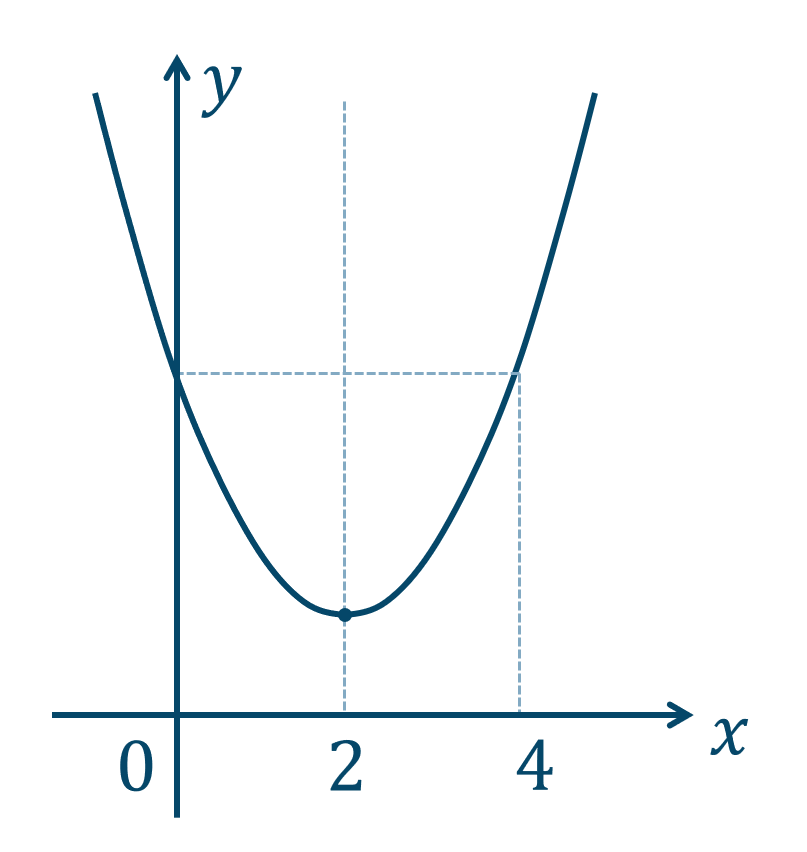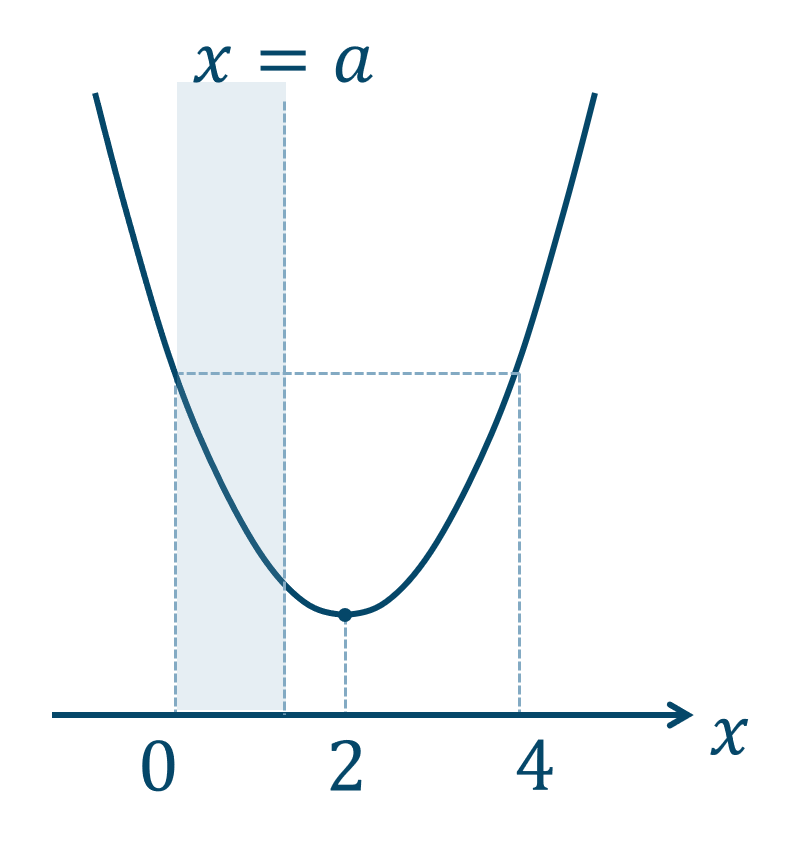定義域の片側が変化する2次関数
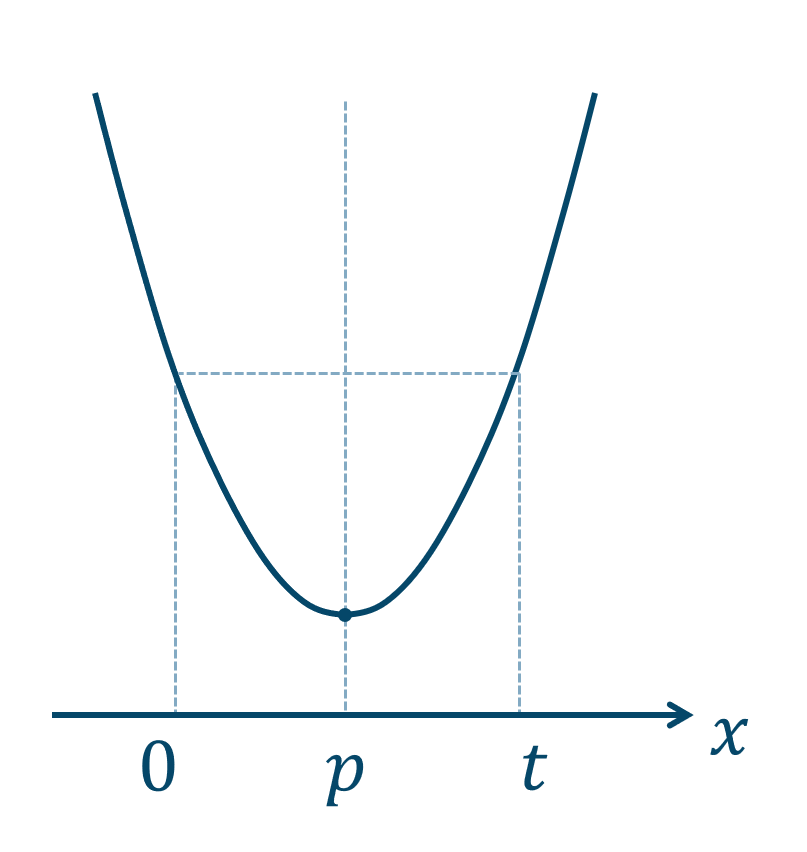
グラフより、\(x=0\) のときと同じ\(y\) の値をとる \(x=t\) を対称性より求めます。
3点 \(0~,~p~,~t\) より、変数 \(a\) がどの位置にあるかで場合分けをして考えましょう。
問題解説:定義域が変化する2次関数の最大値・最小値
与えられた2次関数を平方完成すると、$$\hspace{ 10 pt}y=x^2-4x+3$$$$\hspace{ 18 pt}=x^2-4x+4-4+3$$$$\hspace{ 18 pt}=(x-2)^2-1$$よって、頂点の座標が$$~~~(2~,~-1)$$となります。
定義域の端 \(0\) と軸 \(x=2\) より、\(x=0\) のときと \(y\) 座標が同じになるのは、対称性より \(x=4\) となります。
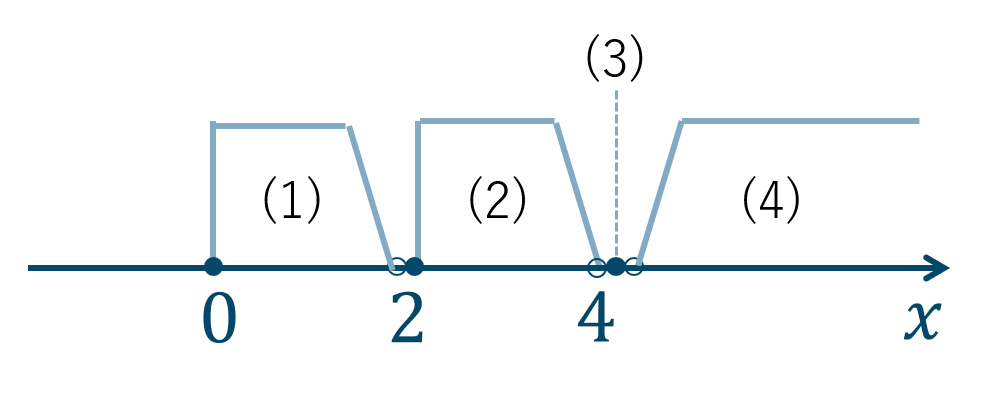
よって、\(x=0~,~2~,~4\) で4つの範囲に分けると、
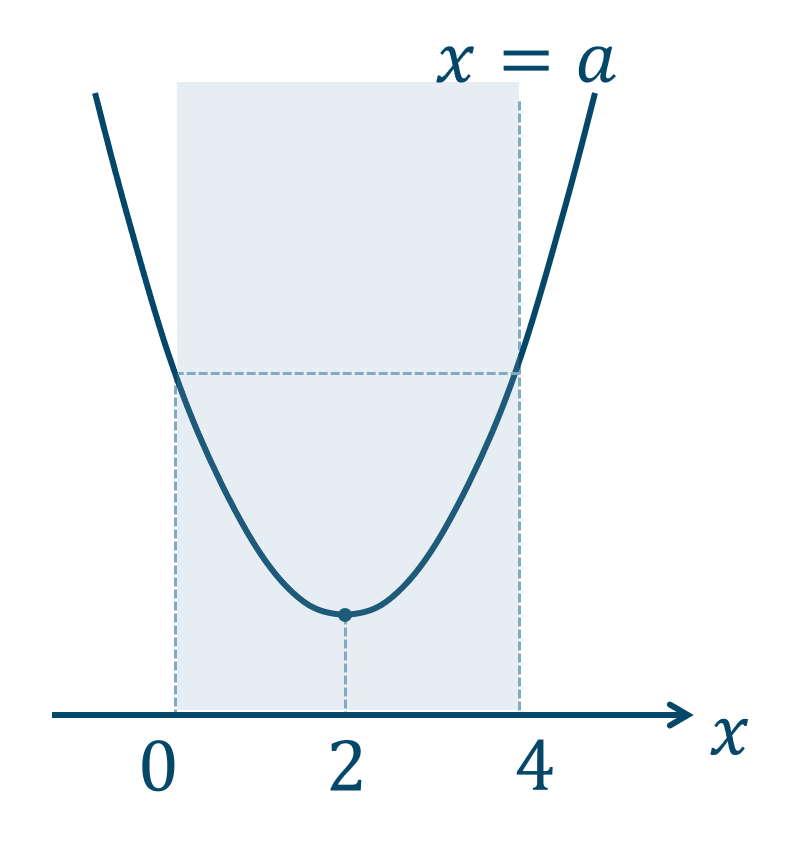
(1) \(0 < a < 2\) のとき、
グラフより、
\(x=0\) で最大値、\(x=a\) で最小値となります。
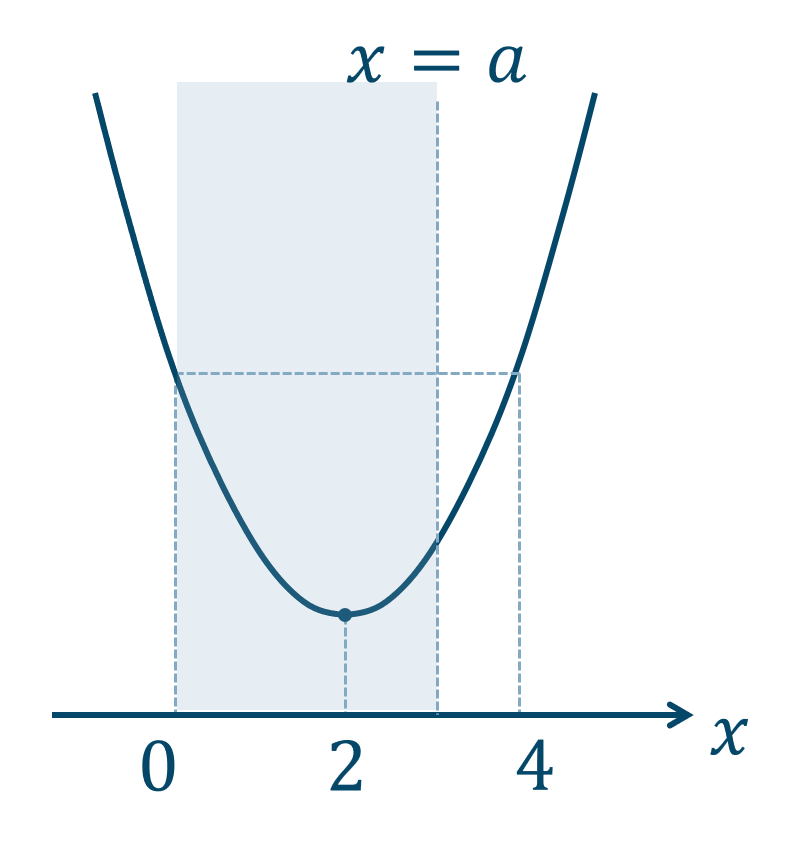
(2) \(2≦a < 4\) のとき、
グラフより、
\(x=0\) で最大値、\(x=2\) で最小値となります。
(3) \(a=4\) のとき、
グラフより、
\(x=0~,~a\) で最大値、\(x=2\) で最小値となります。
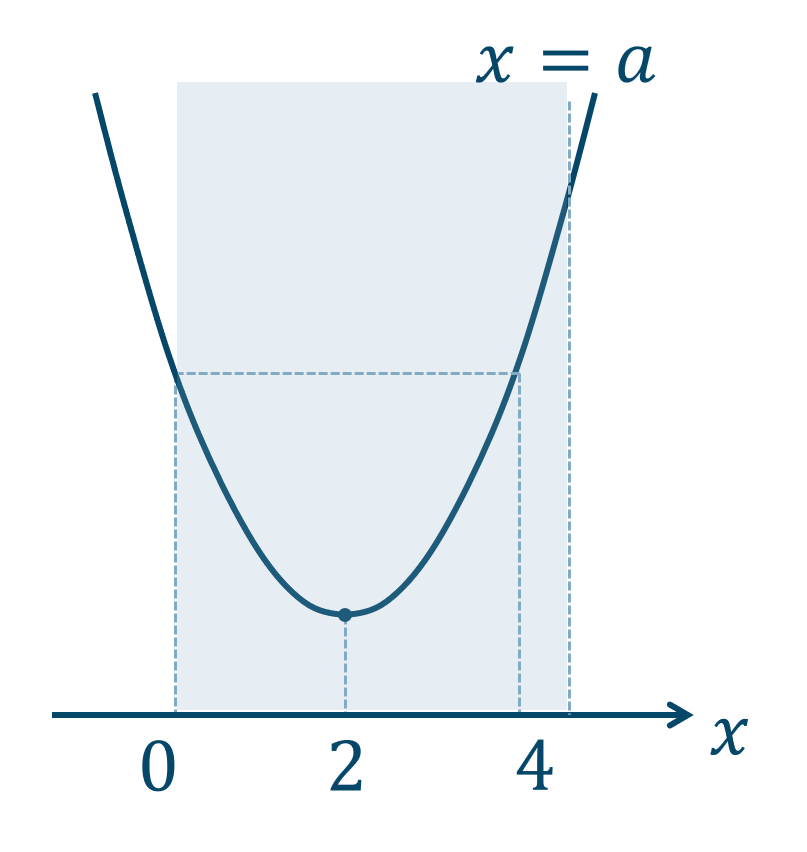
(4) \(a>4\) のとき、
グラフより、
\(x=a\) で最大値、\(x=2\) で最小値となります。
以上より、表にまとめると、
| (1) | (2) | (3) | (4) | |
| 最大値 | \(0 < a < 4\) \(x=0\) |
\(a=4\) \(x=0~,~a\) |
\(a>4\) \(x=a\) |
|
| 最小値 | \(0 < a < 2\) \(x=a\) |
\(a≧2\) \(x=2\) |
||
したがって、最大値は、
( ⅰ ) \(0 < a < 4\) のとき
\(x=0\) で最大値となり、そのときの \(y\) の値は、$$\hspace{ 10 pt}y=0^2-4\cdot0+3=3$$( ⅱ ) \(a=4\) のとき
\(x=0~,~a\) で最大値となり、その値は \(3\)
( ⅲ ) \(a>4\) のとき
\(x=a\) で最大値となり、そのときの \(y\) の値は、$$\hspace{ 10 pt}y=a^2-4a+3$$
また、最小値は、
( ⅰ ) \(0 < a < 2\) のとき
\(x=a\) で最小値となり、そのときの \(y\) の値は、$$\hspace{ 10 pt}y=a^2-4a+3$$( ⅱ ) \(a≧2\) のとき
\(x=2\) で最小値となり、そのときの \(y\) の値は頂点の \(y\) 座標より 、 \(-1\)
したがって、答えは
最大値が
( ⅰ ) \(0 < a < 4\) のとき$$~~~3~~~(x=0)$$( ⅱ ) \(a=4\) のとき$$~~~3~~~(x=0~,~a)$$( ⅲ ) \(a>4\) のとき$$~~~a^2-4a+3~~~(x=a)$$最小値が
( ⅰ ) \(0 < a < 2\) のとき$$~~~a^2-4a+3~~~(x=a)$$( ⅱ ) \(a≧2\) のとき$$~~~-1~~~(x=2)$$となります。
今回のまとめ
定義域が変化する2次関数の最大値・最小値でも場合分けが重要となります。軸と定義域より、場合分けができるようになりましょう。