直角三角形と三角比
正弦を \(\sin{}\) で表し、
余弦を \(\cos{}\) で表し、
正接を \(\tan{}\) で表し、
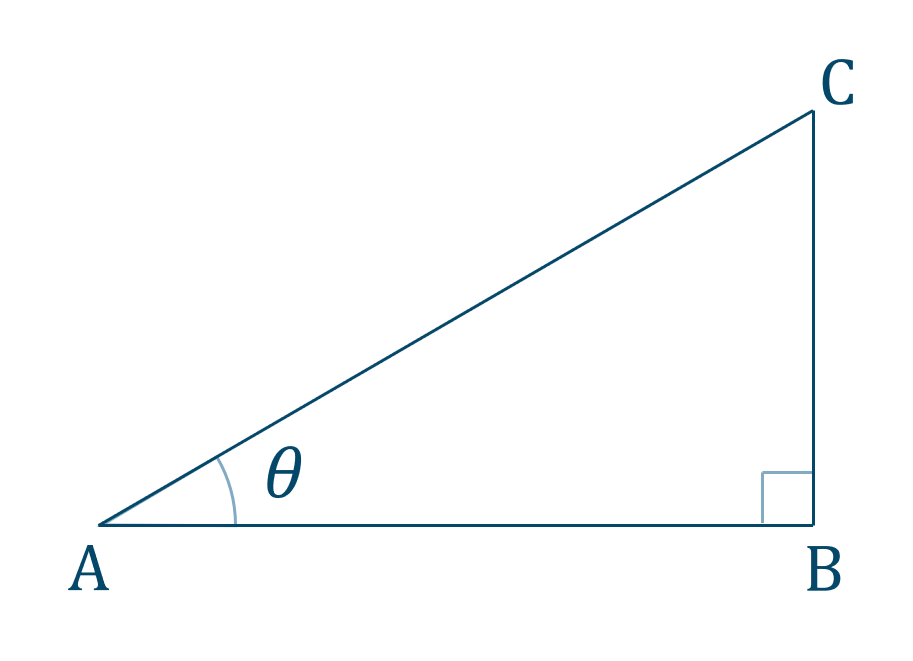
三角比の値を直角三角形より求めるときは、その角を左下の位置にした三角形を描くようにしましょう。
問題解説:直角三角形と三角比
問題解説(1)
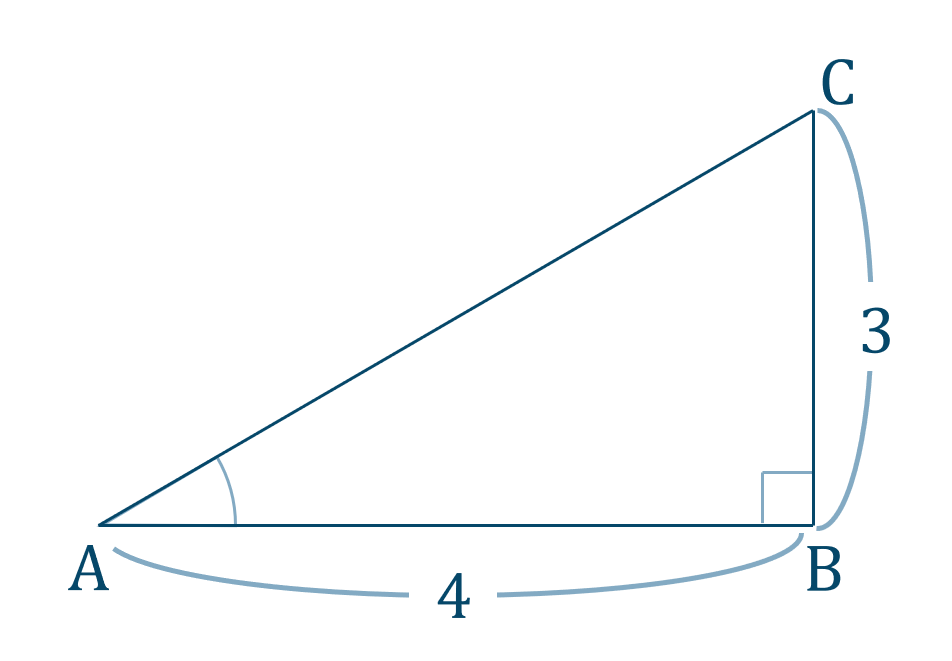
与えられた図形を表すと次のようになります。
\(\triangle {\rm ABC}\) において、三平方の定理を用いると、$$\hspace{ 10 pt}{\rm AC}^2=4^2+3^2$$$$\hspace{ 32 pt}=16+9$$$$\hspace{ 32 pt}=25$$よって、\({\rm AC}>0\) より、$$\hspace{ 10 pt}{\rm AC}=5$$
よって、三角比の定義より、$$\hspace{ 10 pt}\sin{{\rm A}}=\frac{{\rm BC}}{{\rm AC}}$$値を代入すると、$$\hspace{ 10 pt}\sin{{\rm A}}=\frac{3}{5}$$よって、答えは$$~~~\sin{{\rm A}}=\frac{3}{5}$$となります。
問題解説(2)
三角比の定義より、$$\hspace{ 10 pt}\cos{{\rm A}}=\frac{{\rm AB}}{{\rm AC}}$$値を代入すると、$$\hspace{ 10 pt}\cos{{\rm A}}=\frac{4}{5}$$よって、答えは$$~~~\cos{{\rm A}}=\frac{4}{5}$$となります。
問題解説(3)
三角比の定義より、$$\hspace{ 10 pt}\tan{{\rm A}}=\frac{{\rm AC}}{{\rm AB}}$$値を代入すると、$$\hspace{ 10 pt}\tan{{\rm A}}=\frac{3}{4}$$よって、答えは$$~~~\tan{{\rm A}}=\frac{3}{4}$$となります。
問題解説(4)
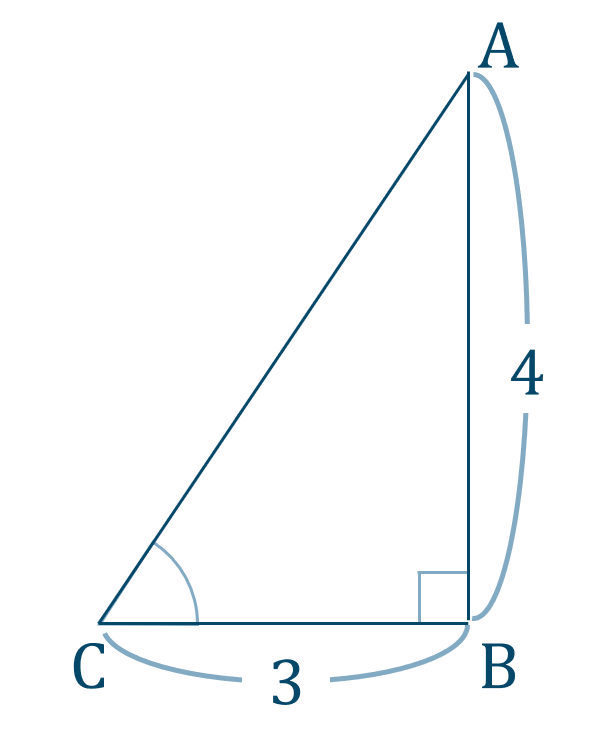
\(\angle{\rm C}\) が左下にくるように図を描きなおすと、
よって、三角比の定義より、$$\hspace{ 10 pt}\tan{{\rm C}}=\frac{{\rm AB}}{{\rm CB}}$$値を代入すると、$$\hspace{ 10 pt}\tan{{\rm C}}=\frac{4}{3}$$よって、答えは$$~~~\tan{{\rm C}}=\frac{4}{3}$$となります。
今回のまとめ
三角比の定義は値の求め方と、角を左下にして直角三角形を描くことを覚えておきましょう。