余角の公式 (90°-θ)
Point：余角の公式単位円上に \(\theta\) と \(90^\circ-\theta\) を表すと、
図の①と②は合同な三角形であるので、
図の①と②は合同な三角形であるので、
$$\sin{(90^\circ-\theta)}=\cos{\theta}$$$$\cos{(90^\circ-\theta)}=\sin{\theta}$$
が成り立ちます。
また、傾きは \(y=x\) で対称となっているので逆数となり、
$$\tan{(90^\circ-\theta)}=\frac{1}{\tan{\theta}}$$
となります。
問題解説：余角の公式
問題解説(1)
問題次の三角比を \(45^\circ\) 以下の三角比で表せ。$${\small (1)}~\sin{85^\circ}$$
\(85^\circ=90^\circ-5^\circ\) であるので、
$$~~~~~~\sin{85^\circ}$$$$~=\sin{(90^\circ-5^\circ)}$$$$~=\cos{5^\circ}$$よって、答えは$$~~~\cos{5^\circ}$$となります。
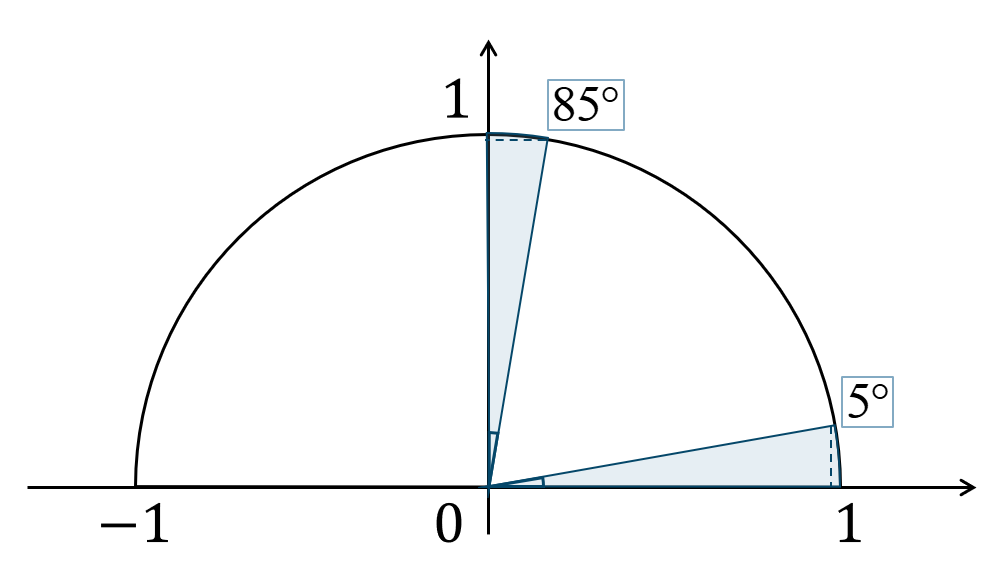
問題解説(2)
問題次の三角比を \(45^\circ\) 以下の三角比で表せ。$${\small (2)}~\cos{63^\circ}$$
\(63^\circ=90^\circ-27^\circ\) であるので、
$$~~~~~~\cos{63^\circ}$$$$~=\cos{(90^\circ-27^\circ)}$$$$~=\sin{27^\circ}$$よって、答えは$$~~~\sin{27^\circ}$$となります。
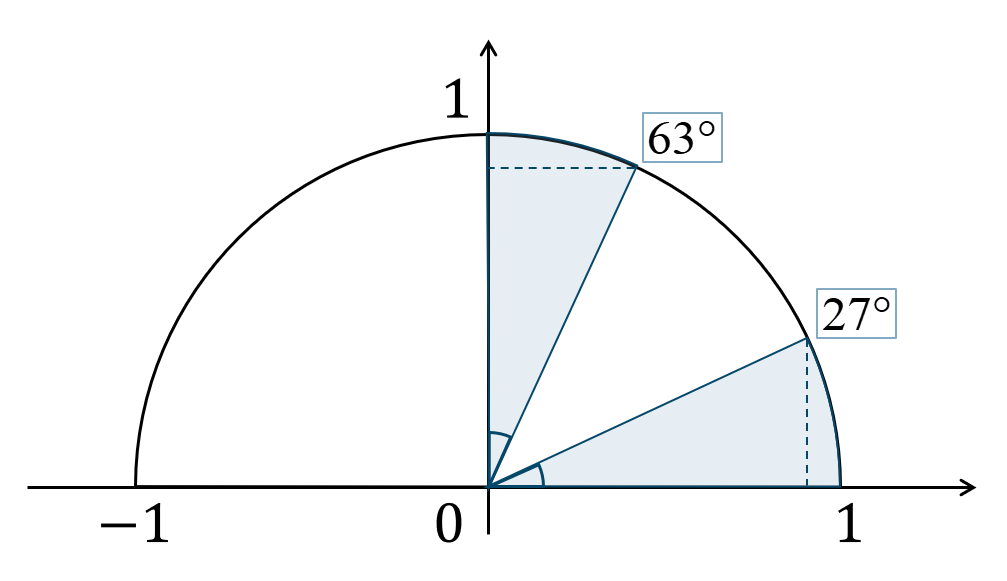
問題解説(3)
問題次の三角比を \(45^\circ\) 以下の三角比で表せ。$${\small (3)}~\tan{71^\circ}$$
\(71^\circ=90^\circ-19^\circ\) であるので、
$$~~~~~~\tan{71^\circ}$$$$~=\tan{(90^\circ-19^\circ)}$$$$~=\frac{1}{\tan{19^\circ}}$$よって、答えは$$~~~\frac{1}{\tan{19^\circ}}$$となります。
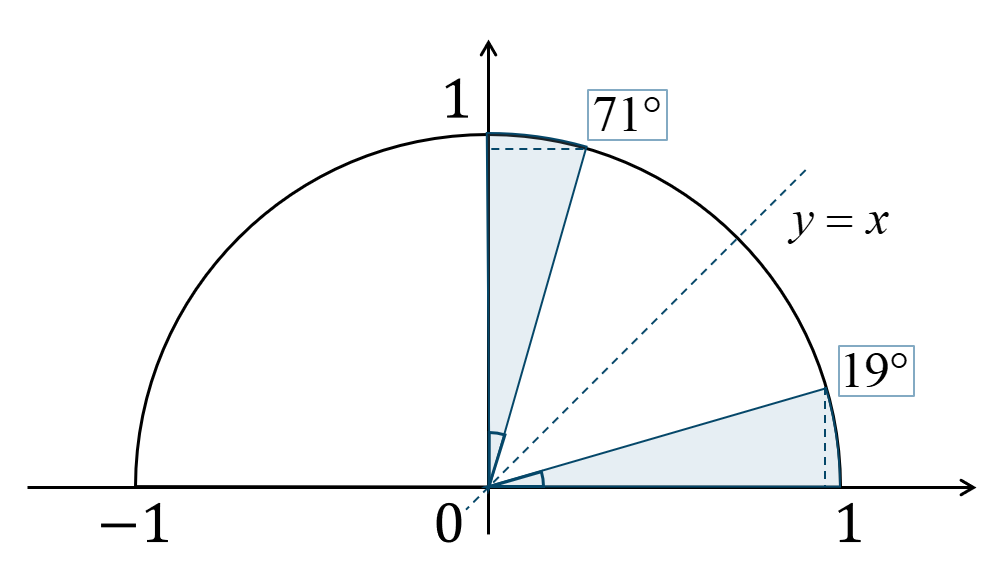
今回のまとめ
覚えにくい三角比の公式である余角の公式ですが、単純暗記するのではなく、単位円上に表す方法で覚えておきましょう。
【問題一覧】数学Ⅰ：図形と計量
このページは「高校数学Ⅰ：図形と計量」の問題一覧ページとなります。解説の見たい単元名がわからないとき...
yorikuwa.com
