三角比の拡張

三角比の拡張（0°から180°）
問題解説：三角比の拡張
今回のまとめ

三角比の拡張（0°から180°）

Point：三角比の拡張$\theta$ が $0^\circ≦\theta≦180^\circ$ の範囲のときの値も単位円を用いて求めることができます。
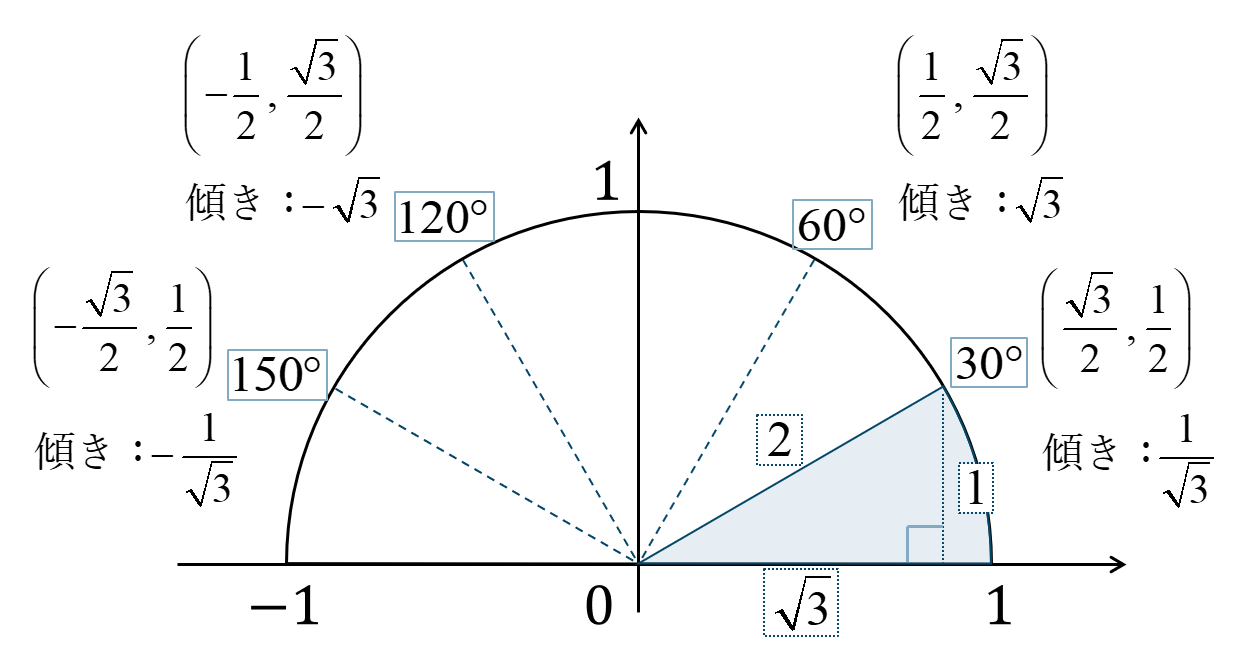
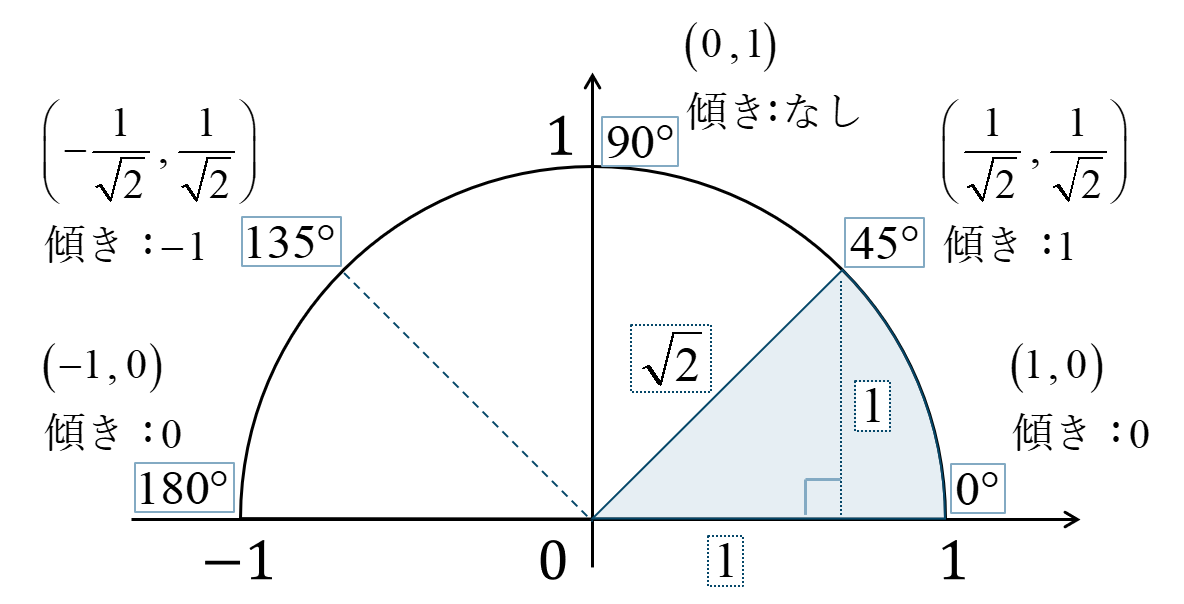
半径 $1$ の円を単位円といい、$x$ 軸との正の部分とのなす角を $\theta$ としたとき、

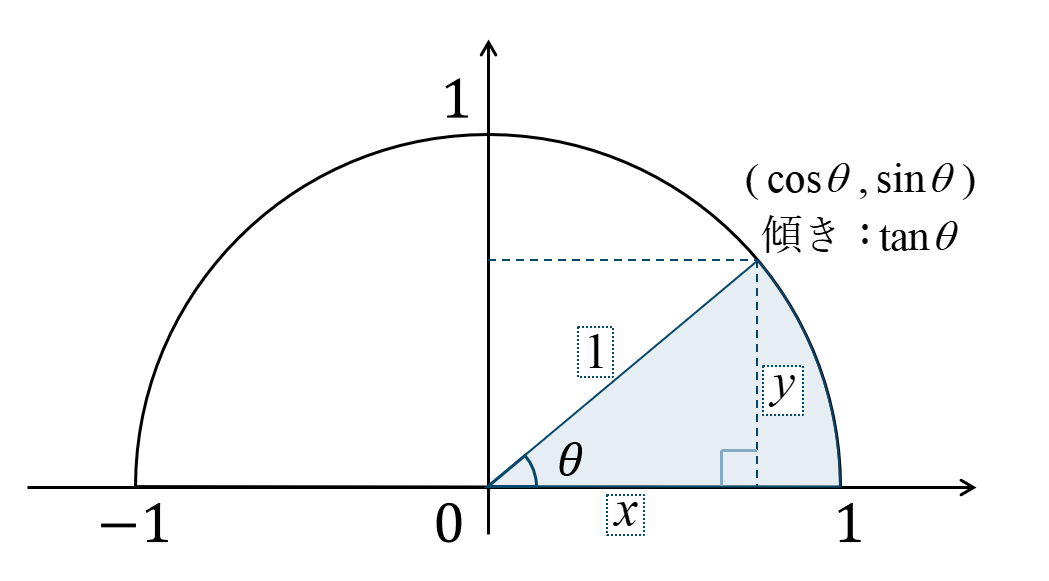
点 ${\rm P}$ の座標が次のようになります。

$${\rm P}(\cos{\theta}~,~\sin{\theta})$$

また、直線 ${\rm OP}$ の傾き $m$ とすると、

$$m=\tan{\theta}$$

となります。

$30^\circ \times n$ の角の場合

$45^\circ \times n$ の角の場合

問題解説：三角比の拡張

問題解説(1)

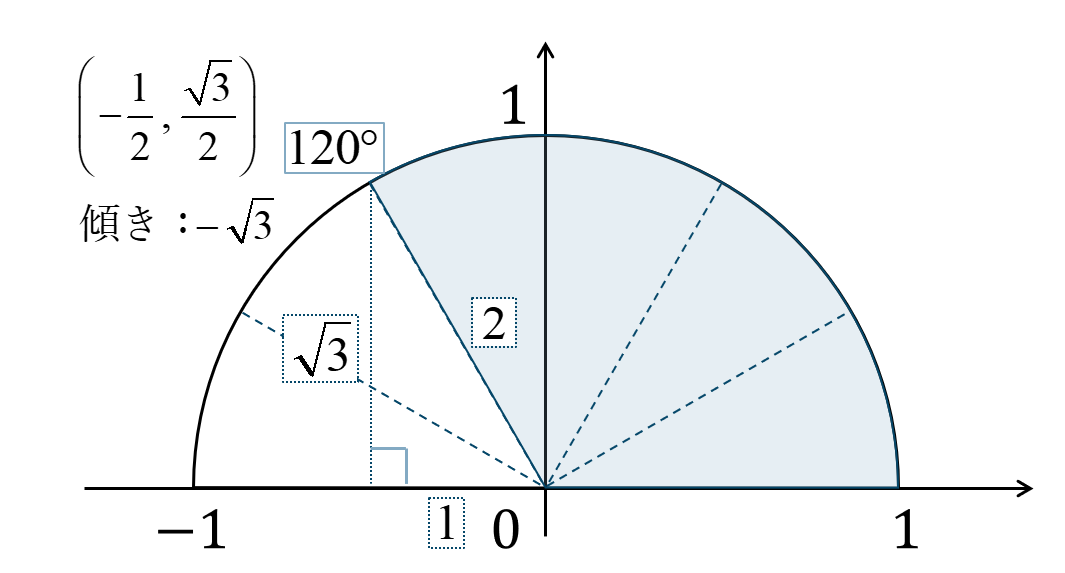
問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (1)}~120^\circ$$

単位円上に角を表すと次のようになりなり、$1:\sqrt{3}:2$ の直角三角形となります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{120^\circ}=\frac{\sqrt{3}}{2}$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{120^\circ}=-\frac{1}{2}$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、$$~~~\tan{120^\circ}=-\sqrt{3}$$となります。
よって、答えは$$~~~\sin{120^\circ}=\frac{\sqrt{3}}{2}~,~\cos{120^\circ}=-\frac{1}{2}$$$$~~~\tan{120^\circ}=-\sqrt{3}$$となります。

問題解説(2)

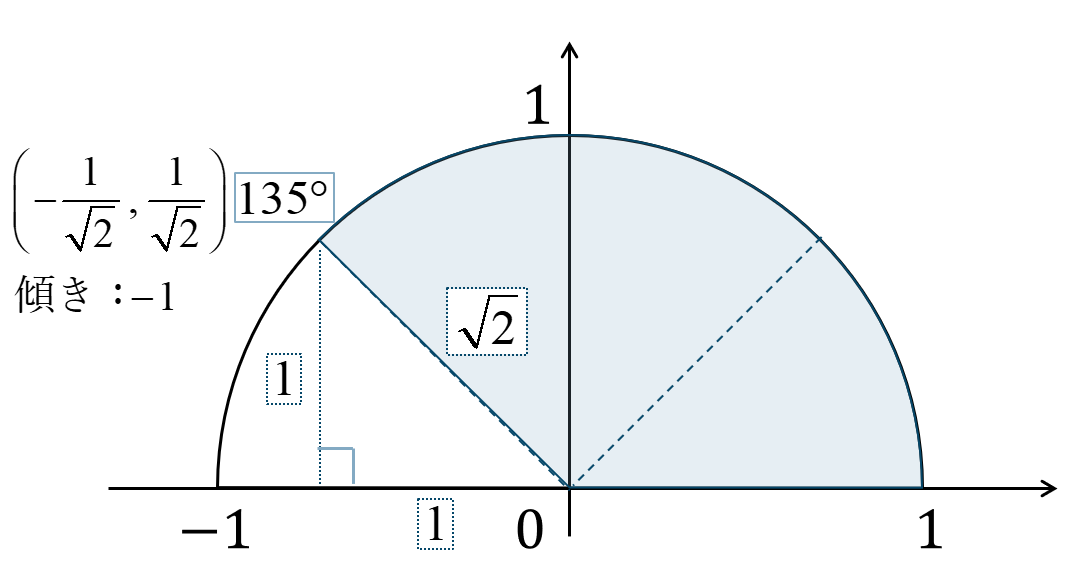
問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (2)}~135^\circ$$

単位円上に角を表すと次のようになり、$1:1:\sqrt{2}$ の直角三角形となります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{135^\circ}=\frac{1}{\sqrt{2}}$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{135^\circ}=-\frac{1}{\sqrt{2}}$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、$$~~~\tan{135^\circ}=-1$$となります。
よって、答えは$$~~~\sin{135^\circ}=\frac{1}{\sqrt{2}}~,~\cos{135^\circ}=-\frac{1}{\sqrt{2}}$$$$~~~\tan{135^\circ}=-1$$となります。

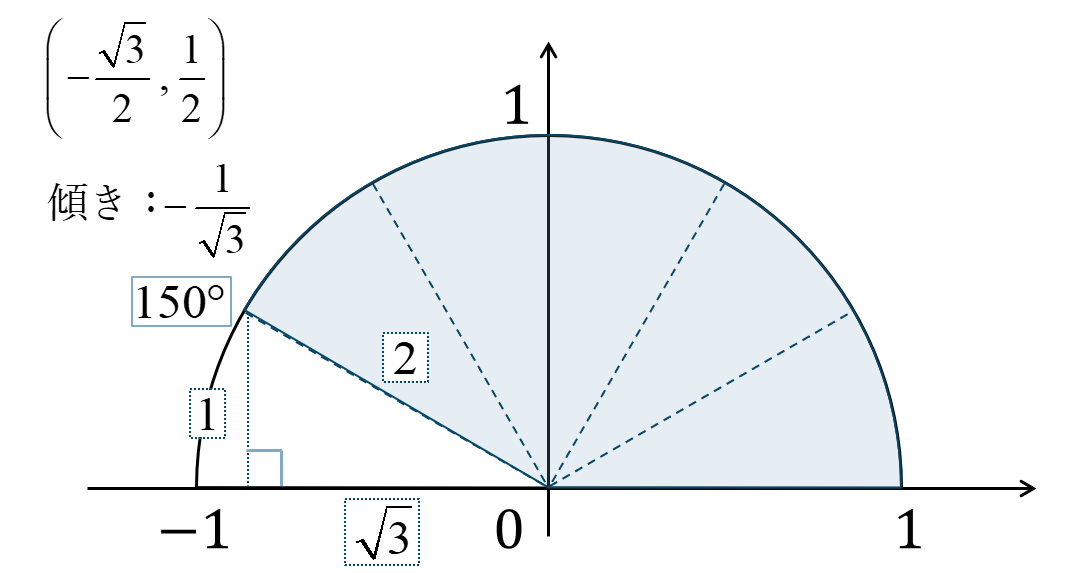
問題解説(3)

問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (3)}~150^\circ$$

単位円上に角を表すと次のようになり、$\sqrt{3}:1:2$ の直角三角形となります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{150^\circ}=\frac{1}{2}$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{150^\circ}=-\frac{\sqrt{3}}{2}$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、$$~~~\tan{150^\circ}=-\frac{1}{\sqrt{3}}$$となります。
よって、答えは$$~~~\sin{150^\circ}=\frac{1}{2}~,~\cos{150^\circ}=-\frac{\sqrt{3}}{2}$$$$~~~\tan{150^\circ}=-\frac{1}{\sqrt{3}}$$となります。

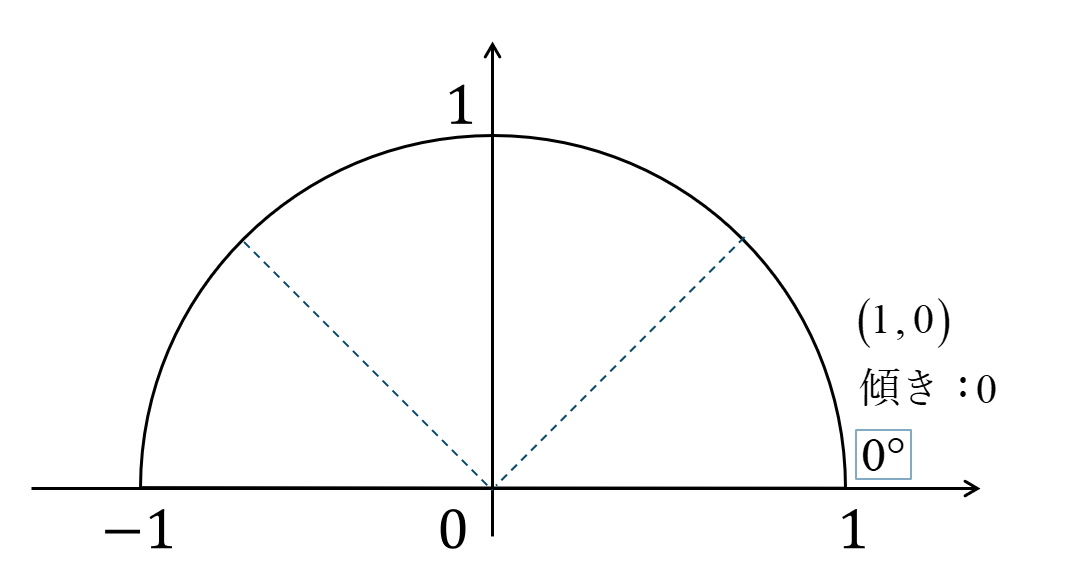
問題解説(4)

問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (4)}~0^\circ$$

単位円上に角を表すと次のようになり、点 $(1~,~0)$ を通ります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{0^\circ}=0$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{0^\circ}=1$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、$$~~~\tan{0^\circ}=0$$となります。
よって、答えは$$~~~\sin{0^\circ}=0~,~\cos{0^\circ}=1$$$$~~~\tan{0^\circ}=0$$となります。

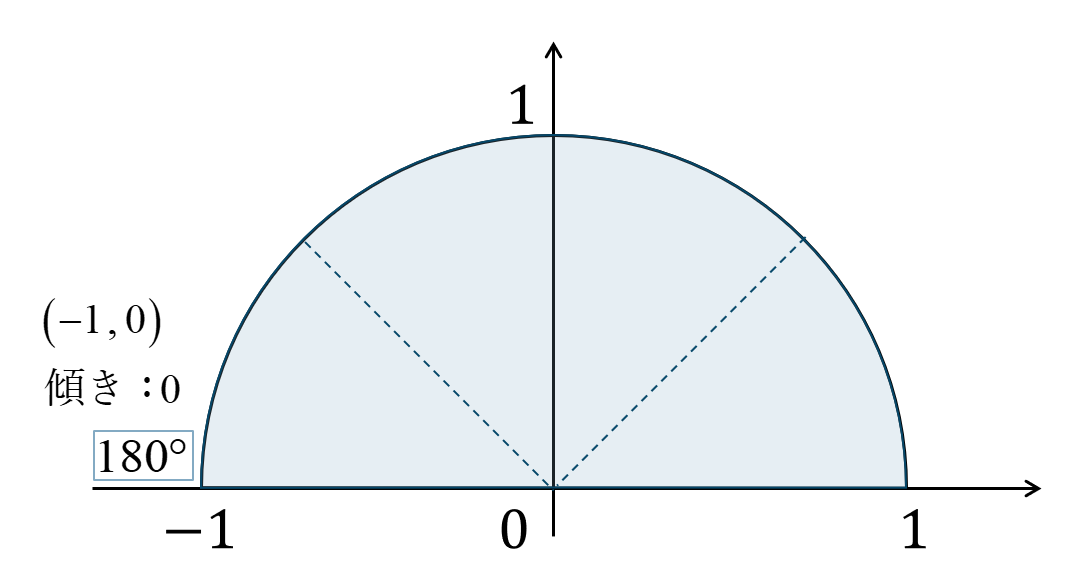
問題解説(5)

問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (5)}~180^\circ$$

単位円上に角を表すと次のようになりなり、点 $(-1~,~0)$ を通ります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{180^\circ}=0$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{180^\circ}=-1$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、$$~~~\tan{180^\circ}=0$$となります。
よって、答えは$$~~~\sin{180^\circ}=0~,~\cos{180^\circ}=-1$$$$~~~\tan{180^\circ}=0$$となります。

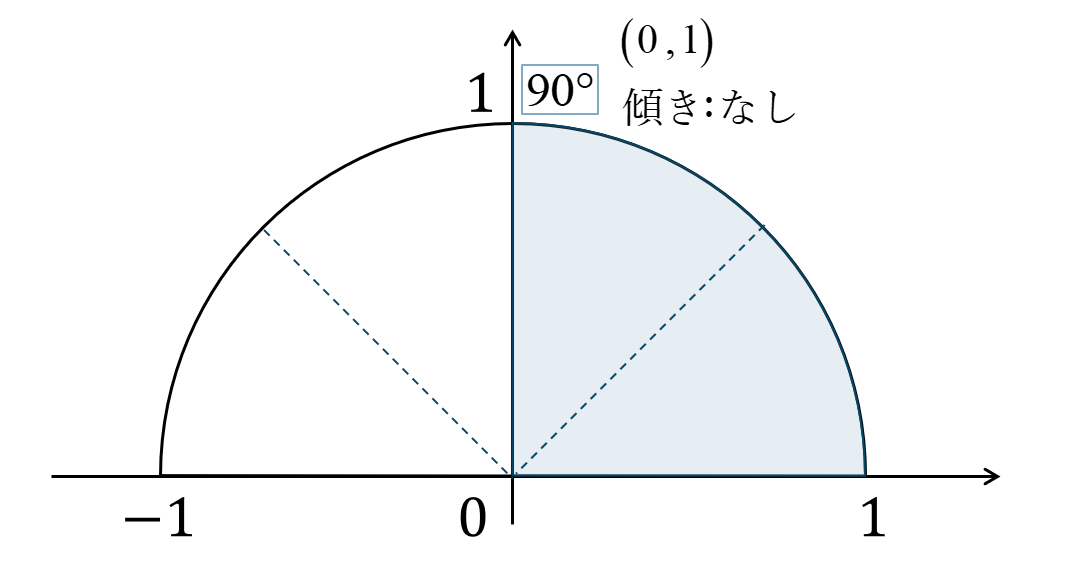
問題解説(6)

問題次の角の $\sin{}$$~,~$$\cos{}$$~,~$$\tan{}$ の値を求めよ。$${\small (6)}~90^\circ$$

単位円上に角を表すと次のようになり、点 $(0~,~-1)$ を通ります。

$\sin{}$ の値は円との交点の $y$ 座標なので、$$~~~\sin{90^\circ}=1$$$\cos{}$ の値は円との交点の $x$ 座標なので、$$~~~\cos{90^\circ}=0$$$\tan{}$ の値は、原点と交点を結ぶ直線の傾きより、「解なし」となります。
よって、答えは$$~~~\sin{90^\circ}=1~,~\cos{90^\circ}=0$$$~~~\tan{0^\circ}$ は解なし
となります。