三角比と２次方程式
Point：三角比と２次方程式三角比１種類だけを用いた２次方程式は、その三角比を \(t\) と置き換えた \(t\) の２次方程式として解きましょう。
また、置き換えたときの \(t\) の値の範囲には注意しましょう。
\(0^\circ≦\theta≦180^\circ\) のとき
( ⅰ ) \(\sin{\theta}=t\) とすると、
よって、$$~~~0≦\sin{\theta}≦1$$となるので、
また、置き換えたときの \(t\) の値の範囲には注意しましょう。
\(0^\circ≦\theta≦180^\circ\) のとき
( ⅰ ) \(\sin{\theta}=t\) とすると、
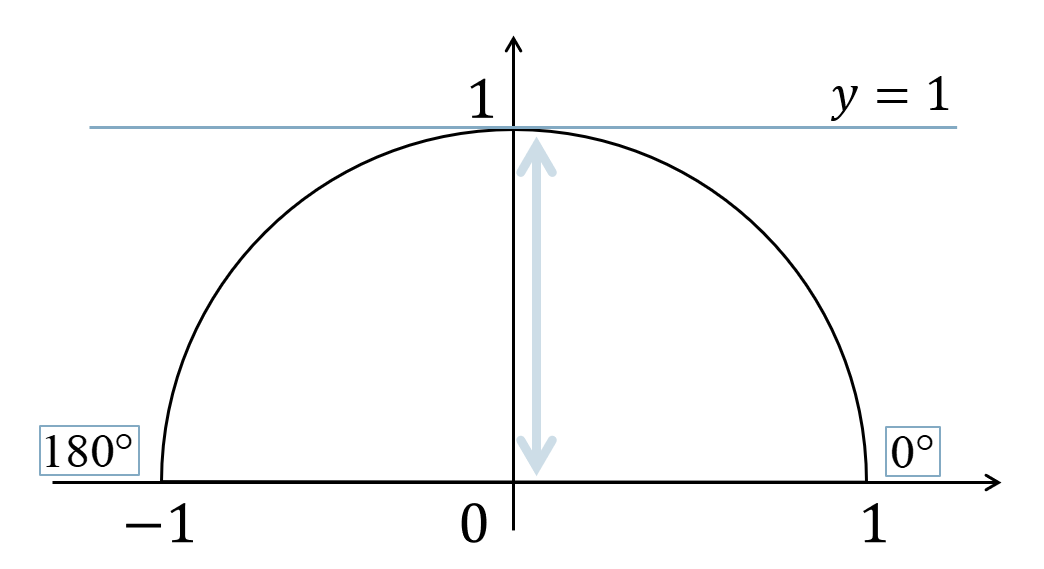
よって、$$~~~0≦\sin{\theta}≦1$$となるので、
$$0≦t≦1$$
となります。
( ⅱ ) \(\cos{\theta}=t\) とすると、
よって、$$~~~-1≦\cos{\theta}≦1$$となるので、
$$-1≦t≦1$$
となります。
問題解説：三角比と２次方程式
問題次の方程式の解を求めよ。ただし、\(0^\circ≦\theta≦180^\circ\) とする。$$~~~2\cos^2{\theta}-\cos{\theta}-1=0$$
\(\cos{\theta}=t\) とすると、\(0^\circ≦\theta≦180^\circ\) であることより、
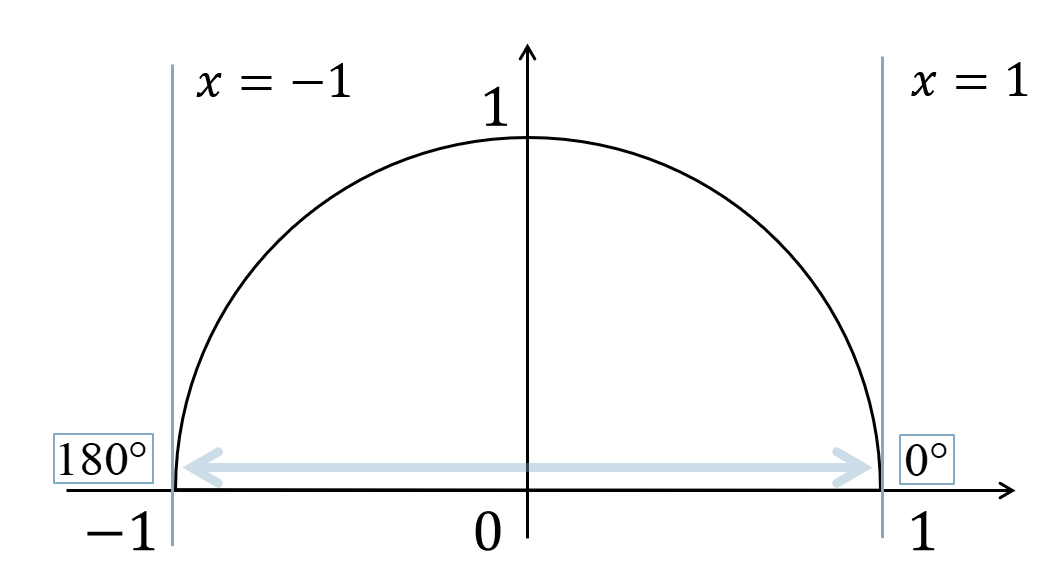
単位円より、$$~~~-1≦\cos{\theta}≦1$$となるので、$$~~~-1≦t≦1$$となります。
与式を \(\cos{\theta}=t\) で置き換えると、$$\hspace{ 10 pt}2t^2-t-1=0$$左辺を因数分解すると、たすき掛けの表より、
$$\hspace{ 10 pt}(2t+1)(t-1)=0$$よって、$$~~~t=-\frac{1}{2}~,~1$$となり、これは \(-1≦t≦1\) を満たします。
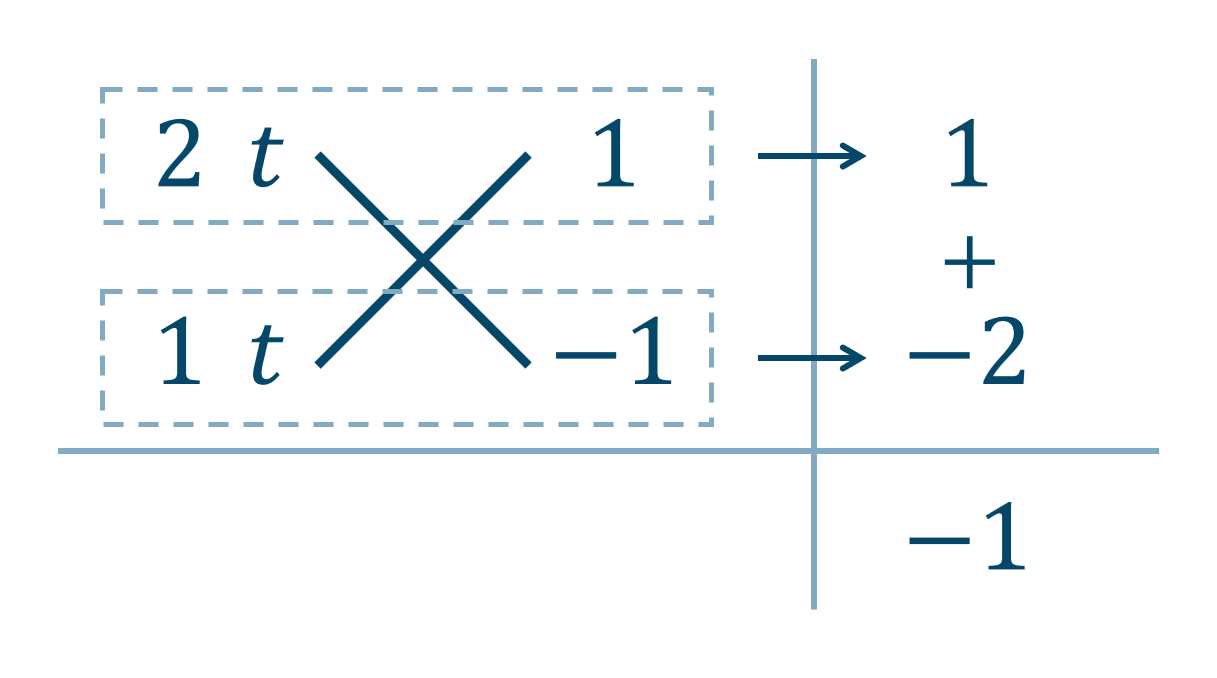
( ⅰ ) \(t=-{\Large \frac{1}{2}}\) のとき、
元に戻すと、$$~~~\cos{\theta}=-\frac{1}{2}$$単位円上に表すと、
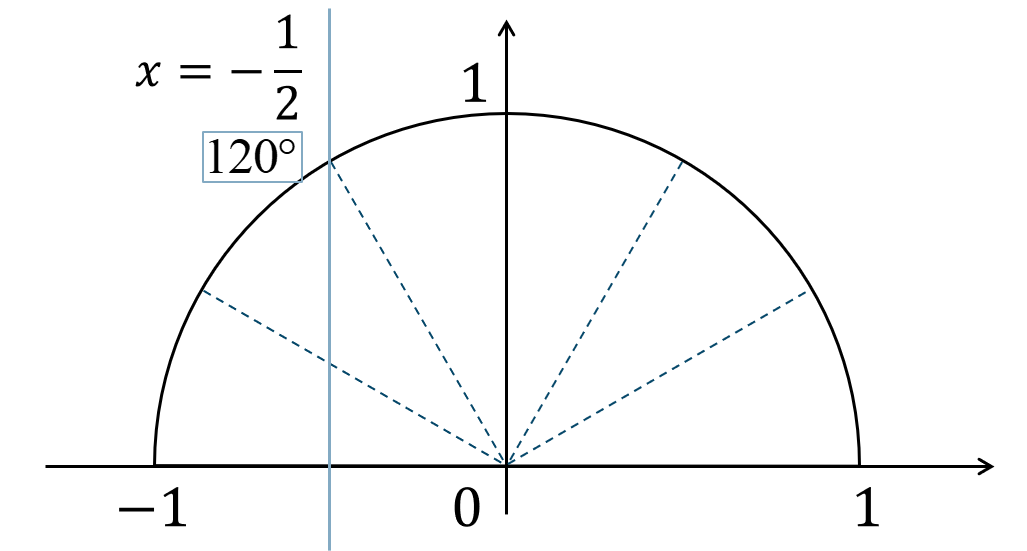
よって、\(\theta=120^\circ\) となります。
( ⅱ ) \(t=1\) のとき、
元に戻すと、$$~~~\cos{\theta}=1$$単位円上に表すと、
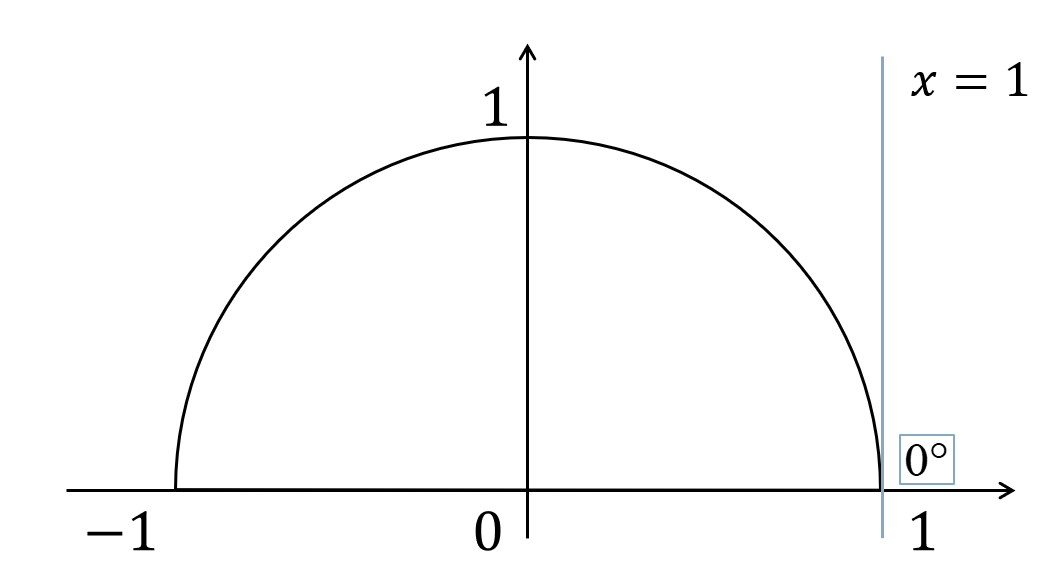
よって、\(\theta=0^\circ\) となります。
したがって、答えは$$~~~\theta=0^\circ~,~120^\circ$$となります。
今回のまとめ
三角比の２次方程式は、三角比を置き換えて文字についての２次方程式として解きましょう。また、置き換えたときの値の範囲には注意しましょう。
【問題一覧】数学Ⅰ：図形と計量
このページは「高校数学Ⅰ：図形と計量」の問題一覧ページとなります。解説の見たい単元名がわからないとき...
yorikuwa.com
