三角比を用いた三角形の面積
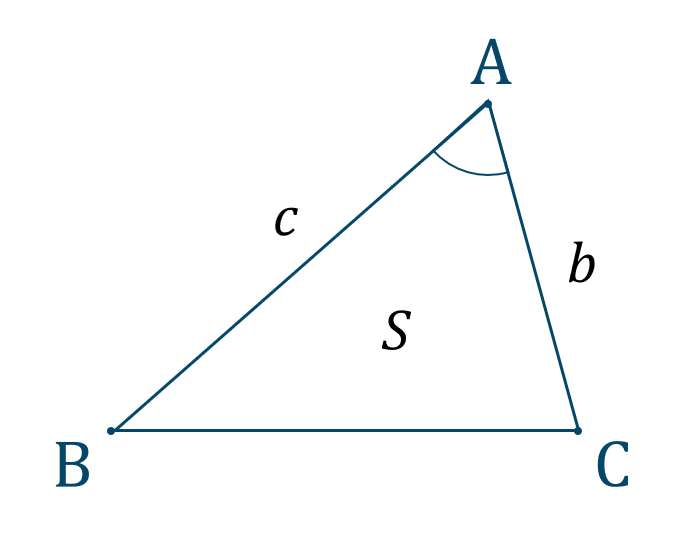
\(\sin{{\rm A}}\) を用いて三角形の面積 \(S\) を求めると、
同様に、\(\sin{{\rm B}}\) を用いると、
\(\sin{{\rm C}}\) を用いると、
このように、「2辺とその間の角」が条件となります。
問題解説:三角形の面積(三角比)
問題解説(1)
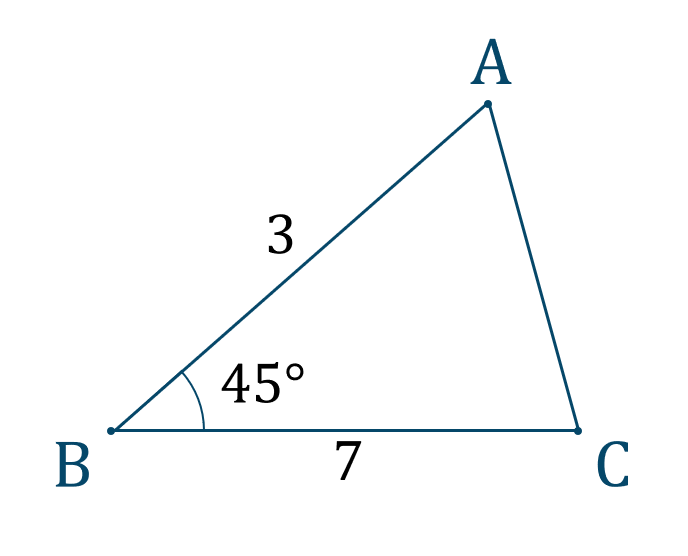
与えられた図形は次のようになります。
三角形の面積を \(S\) とすると、$$~~~S=\frac{1}{2}ca\sin{{\rm B}}$$これより、値を代入すると、$$\hspace{ 10 pt}S=\frac{1}{2}\cdot7\cdot3\cdot\sin{45^\circ}$$$$\hspace{ 20 pt}=\frac{1}{2}\cdot21\cdot\frac{1}{\sqrt{2}}$$$$\hspace{ 20 pt}=\frac{21}{2\sqrt{2}}$$分母分子に \(\sqrt{2}\) をかけると、$$\hspace{ 20 pt}=\frac{21\times\sqrt{2}}{2\sqrt{2}\times\sqrt{2}}$$$$\hspace{ 20 pt}=\frac{21\sqrt{2}}{2\cdot2}$$$$\hspace{ 20 pt}=\frac{21\sqrt{2}}{4}$$よって、答えは$$~~~S=\frac{21\sqrt{2}}{4}$$となります。
問題解説(2)
与えられた図形は次のようになります。
この三角形は \({\rm AB}={\rm AC}\) の二等辺三角形であることより、$$~~~\angle{\rm B}=30^\circ$$よって、三角形の内角の和が \(180^\circ\) より、$$\hspace{ 10 pt}\angle{\rm A}=180^\circ-(\angle{\rm B}+\angle{\rm C})$$$$\hspace{ 28 pt}=180^\circ-(30^\circ+30^\circ)$$$$\hspace{ 28 pt}=180^\circ-60^\circ$$$$\hspace{ 28 pt}=120^\circ$$
したがって、三角形の面積を \(S\) とすると、$$~~~S=\frac{1}{2}bc\sin{{\rm A}}$$これより、数値を代入すると、$$\hspace{ 10 pt}S=\frac{1}{2}\cdot4\cdot4\cdot\sin{120^\circ}$$$$\hspace{ 20 pt}=8\cdot\frac{\sqrt{3}}{2}$$$$\hspace{ 20 pt}=4\sqrt{3}$$よって、答えは$$~~~S=4\sqrt{3}$$となります。
今回のまとめ
三角比を用いた三角形の面積の求め方は、「2辺とその間の角」が条件となっている点に注意して計算しましょう。