散布図と相関
Point:散布図と相関2種類のデータを横軸と縦軸を用いて、点で図示していったものを散布図といいます。
2つの変数 \(x~,~y\) において、
( ⅰ ) 散布図が次のとき

\(y=x\) のグラフに近づくので、
\(x\) と \(y\) に正の相関があるといいます。
( ⅱ ) 散布図が次のとき

\(y=-x\) のグラフに近づくので、
このとき、\(x\) と \(y\) に負の相関があるといいます。
( ⅲ ) 散布図が次のとき

このとき、\(x\) と \(y\) に相関がないといいます。
また、正の相関や負の相関があるとき、直線状に近づくほど相関が強いといい、広がると相関が弱いといいます。
2つの変数 \(x~,~y\) において、
( ⅰ ) 散布図が次のとき
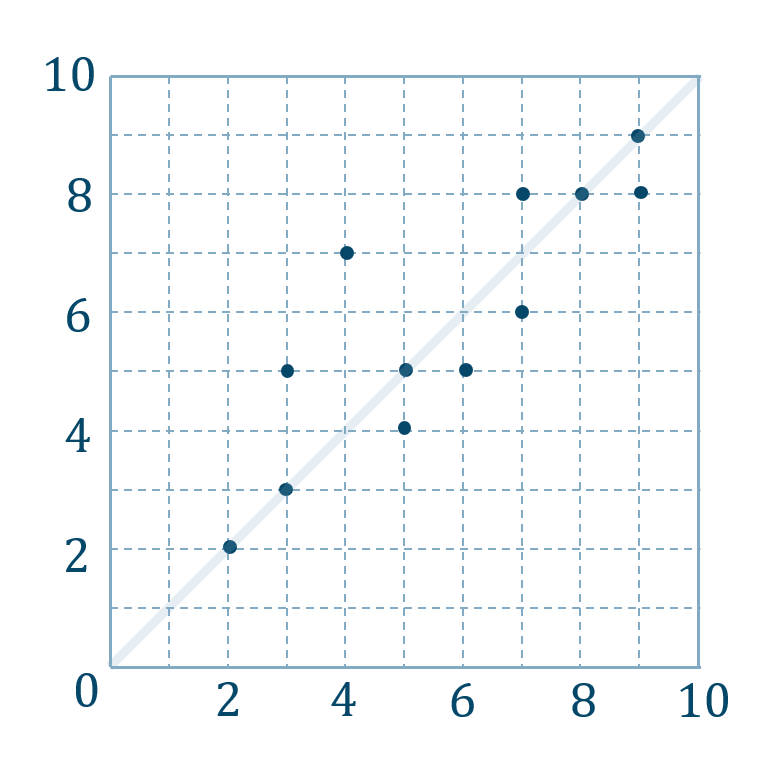
\(y=x\) のグラフに近づくので、
\(x\) と \(y\) に正の相関があるといいます。
( ⅱ ) 散布図が次のとき
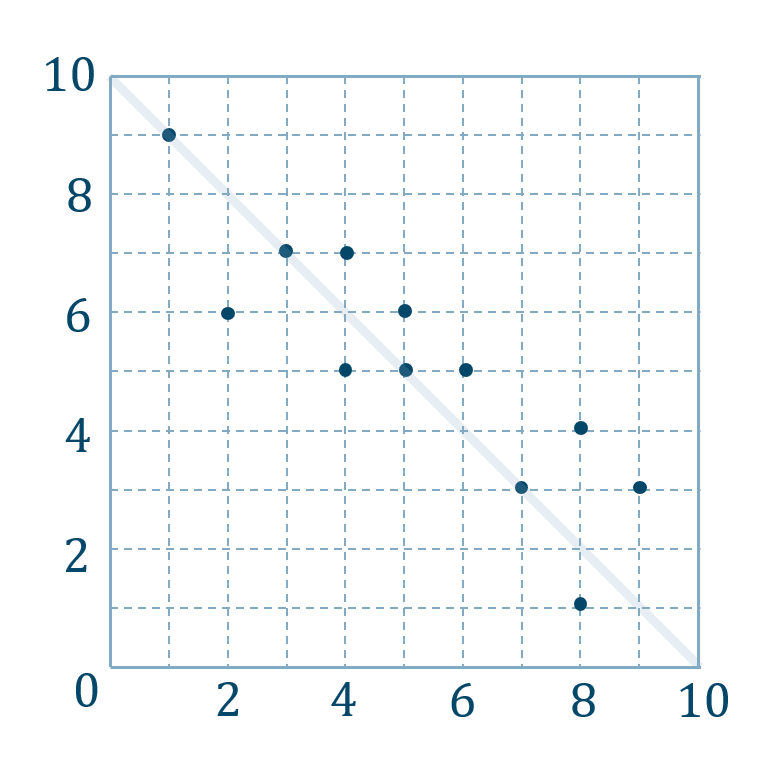
\(y=-x\) のグラフに近づくので、
このとき、\(x\) と \(y\) に負の相関があるといいます。
( ⅲ ) 散布図が次のとき
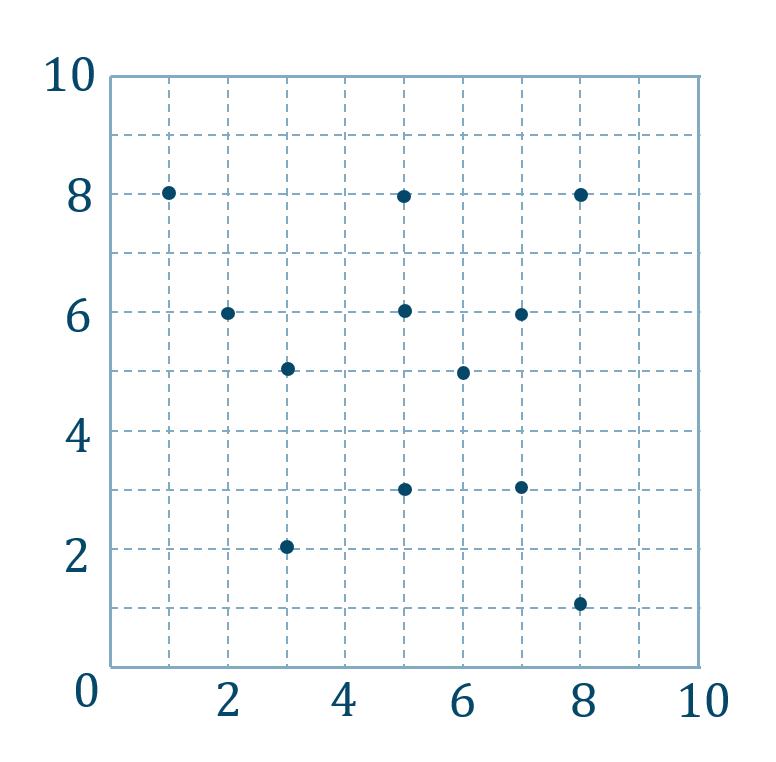
このとき、\(x\) と \(y\) に相関がないといいます。
また、正の相関や負の相関があるとき、直線状に近づくほど相関が強いといい、広がると相関が弱いといいます。
問題解説:散布図と相関
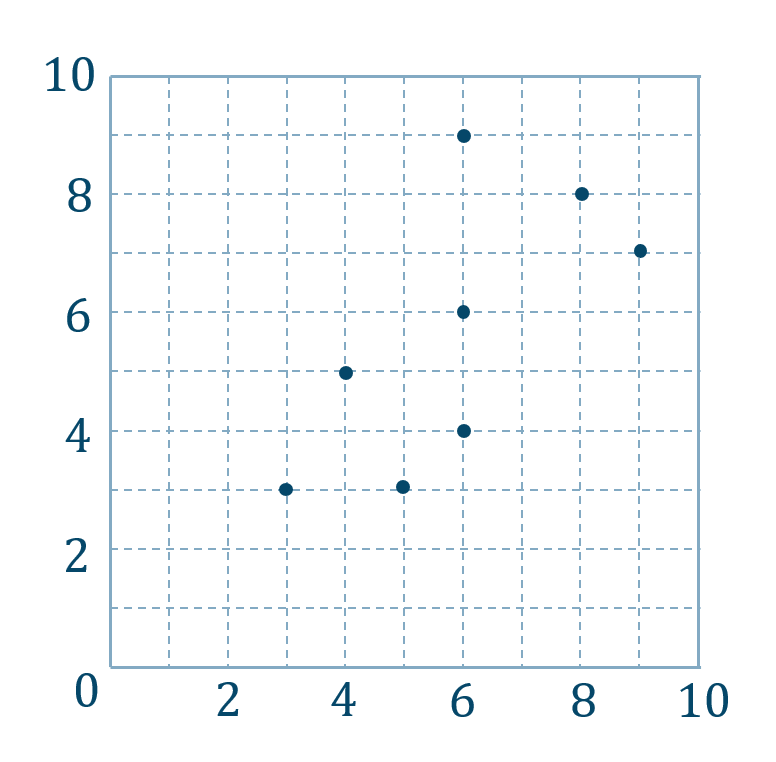
問題次の \(x~,~y\) のデータより散布図をかき相関を調べよ。
| ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ⑧ | |
| \(x\) | \(3\) | \(5\) | \(6\) | \(8\) | \(4\) | \(9\) | \(6\) | \(6\) |
| \(y\) | \(3\) | \(3\) | \(6\) | \(8\) | \(5\) | \(7\) | \(4\) | \(9\) |
データを散布図で表すと次のようになります。
また、この散布図より正の相関があるといえます。
今回のまとめ
2種類のデータから散布図が書けるようになりましょう。また、正の相関や負の相関についてそれぞれの散布図を覚えておきましょう。

【問題一覧】数学Ⅰ:データの分析
このページは「高校数学Ⅰ:データの分析」の問題一覧ページとなります。解説の見たい単元名がわからないと...