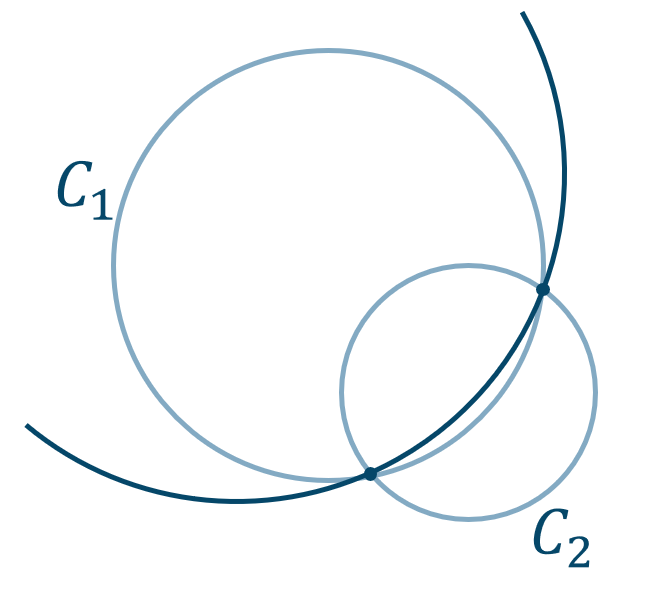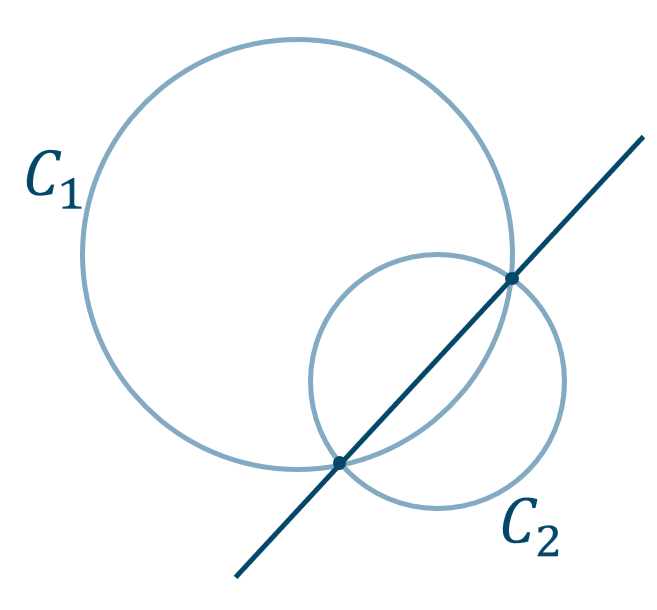2つの円の交点を通る円・直線の解法
2つの円$$~~~\biggl\{ \begin{eqnarray} ~x^2+y^2+l_1x+m_1y+n_1=0 ~\cdots{\small (a)} \\ ~x^2+y^2+l_2x+m_2y+n_2=0~\cdots{\small (b)} \end{eqnarray}$$の交点を通る図形の方程式は、定数 \(k\) を用いて、
と表すことができます。
定数 \(k\) の値は、この円が通る点の座標を代入して求めましょう。
・2つの円の交点を通る直線
上の図形の方程式において、\(k=-1\) を代入すると \(x^2\) と \(y^2\) が消去されて直線の方程式となります。
この直線の方程式が2つの円の交点を通る直線の方程式となります。
問題解説:2つの円の交点を通る円・直線
$$~~~\biggl\{ \begin{eqnarray} ~x^2+y^2-5=0~\cdots{\large ①} \\~x^2+y^2-2x-6y+1=0 ~\cdots{\large ②}\end{eqnarray}$$①と②より、この2つの円の交点を通る図形の方程式は、定数 \(k\) を用いて次のように表します。$$~~~(x^2+y^2-5)k$$$$\hspace{30pt}+(x^2+y^2-2x-6y+1)=0~ \cdots{\large ③}$$これが点 \((2,3)\) を通ることより、代入すると、$$~~~(2^2+3^2-5)k$$$$\hspace{ 39 pt}+(2^2+3^2-2\cdot2-6\cdot3+1)=0$$$$\hspace{ 10 pt}(4+9-5)k+(4+9-4-18+1)=0$$$$\hspace{ 10 pt}8k+(-8)=0$$移項して、両辺を \(8\) で割ると、$$\hspace{ 10 pt}8k=8$$$$\hspace{ 16 pt}k=1$$これを③の式に代入すると、$$~~~(x^2+y^2-5)\cdot1$$$$\hspace{58pt}+(x^2+y^2-2x-6y+1)=0$$$$\hspace{ 10 pt}x^2+y^2-5+x^2+y^2-2x-6y+1=0$$$$\hspace{ 10 pt}2x^2+2y^2-2x-6y-4=0$$両辺を \(2\) で割ると、$$\hspace{ 10 pt}x^2+y^2-x-3y-2=0$$よって、求める円の方程式は、$$~~~x^2+y^2-x-3y-2=0$$となります。
また、①と②の交点を通る直線の方程式は、③の式において \(k=-1\) のときであるので、$$~~~(x^2+y^2-5)\cdot (-1)$$$$\hspace{50pt}+(x^2+y^2-2x-6y+1)=0$$$$\hspace{ 10 pt}-x^2-y^2+5$$$$\hspace{50pt}+x^2+y^2-2x-6y+1=0$$$$\hspace{ 10 pt}-2x-6y+6=0$$両辺を \(-2\) で割ると、$$\hspace{ 10 pt}x+3y-3=0$$よって、求める直線の方程式は、$$~~~x+3y-3=0$$となります。
今回のまとめ
2つの円の交点を通る円の方程式は、定数 \(k\) を用いた式を覚えておきましょう。また、直線の方程式になる条件 \(k=-1\) も忘れないようにしましょう。