三角関数の値（単位円）

単位円と三角関数の値
問題解説：三角関数の値（単位円）
今回のまとめ

単位円と三角関数の値

Point：単位円と三角関数の値単位円上の点 $P$ の座標が $(\cos{\theta}~,~\sin{\theta})$ となり、
原点と点 $P$ を結んだ直線の傾きが $\tan{\theta}$ となります。
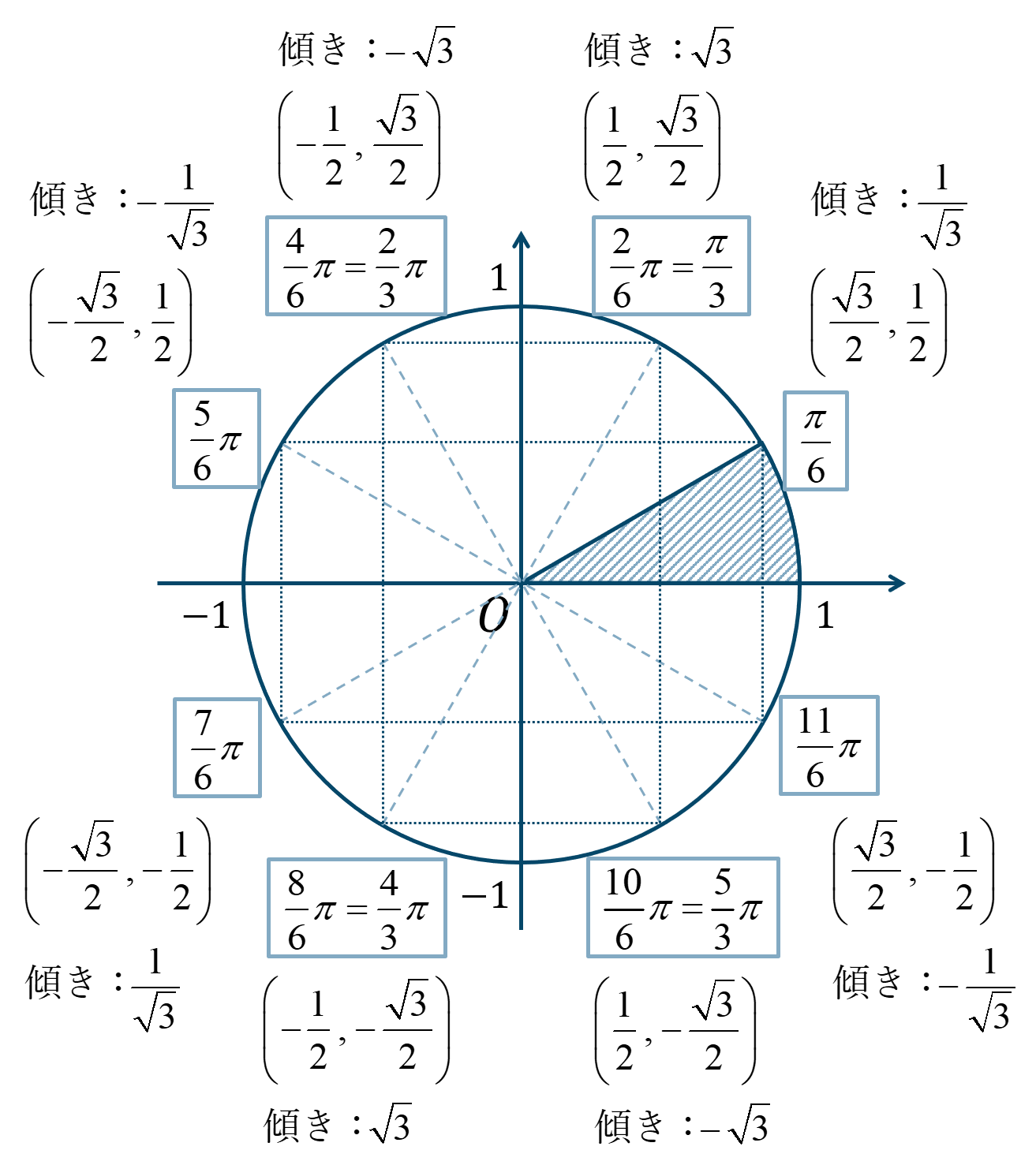
・ ${\Large \frac{\pi}{6}}$ の倍数の角
与えられた角を ${\Large \frac{\pi}{6}}$ の何個分かを考えて、単位円上の位置を確認します。

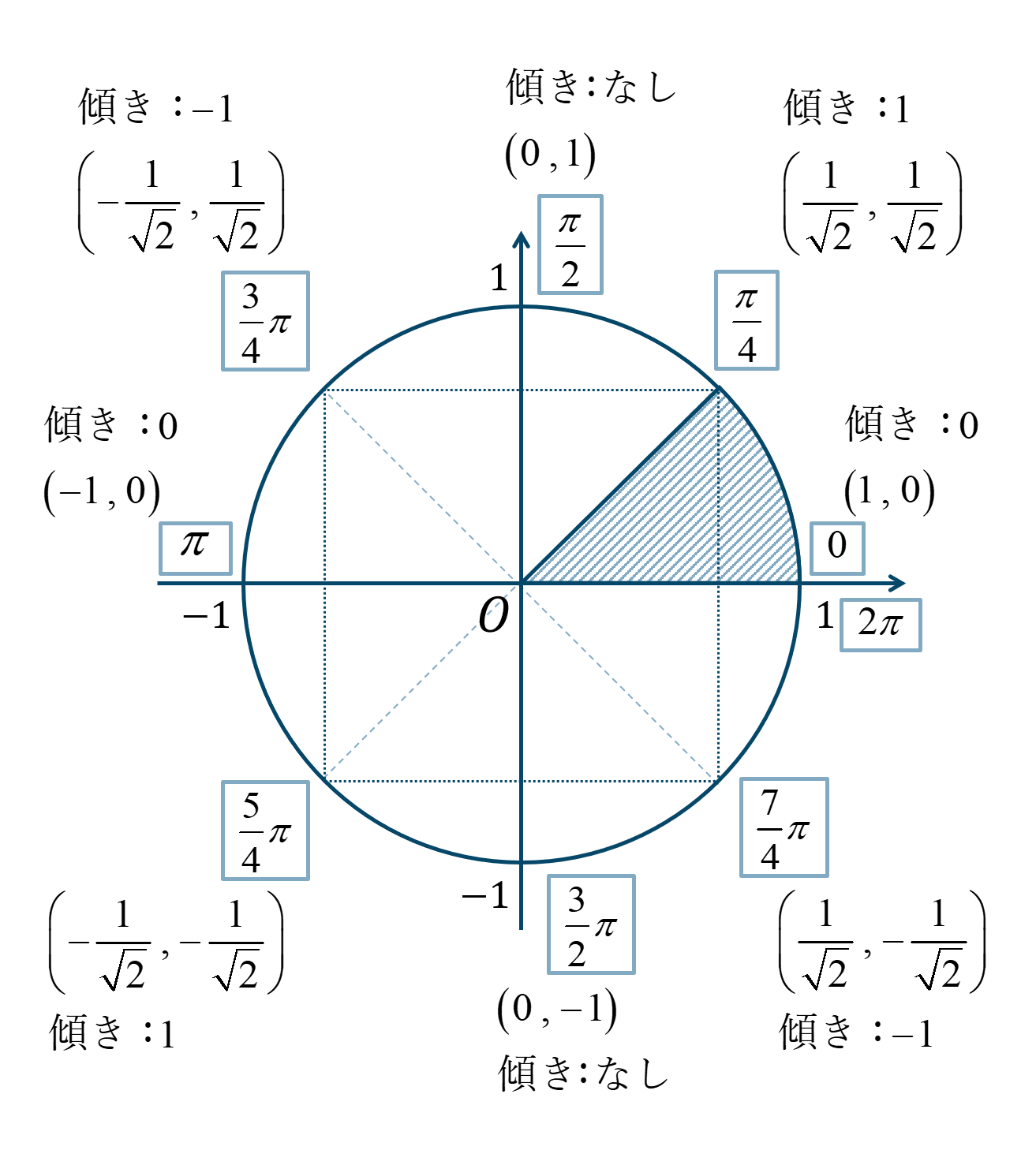
・ ${\Large \frac{\pi}{4}}$ の倍数の角
与えられた角を ${\Large \frac{\pi}{4}}$ の何個分かを考えて、単位円上の位置を確認します。

これらの２つの表の使い方は、
例えば、${\Large \frac{4}{3}}\pi$ のとき、
${\Large \frac{4}{3}}\pi={\Large \frac{8}{6}}\pi$ より ${\Large \frac{\pi}{6}}$ が8個分と考えて、単位円上の位置は次のようになります。

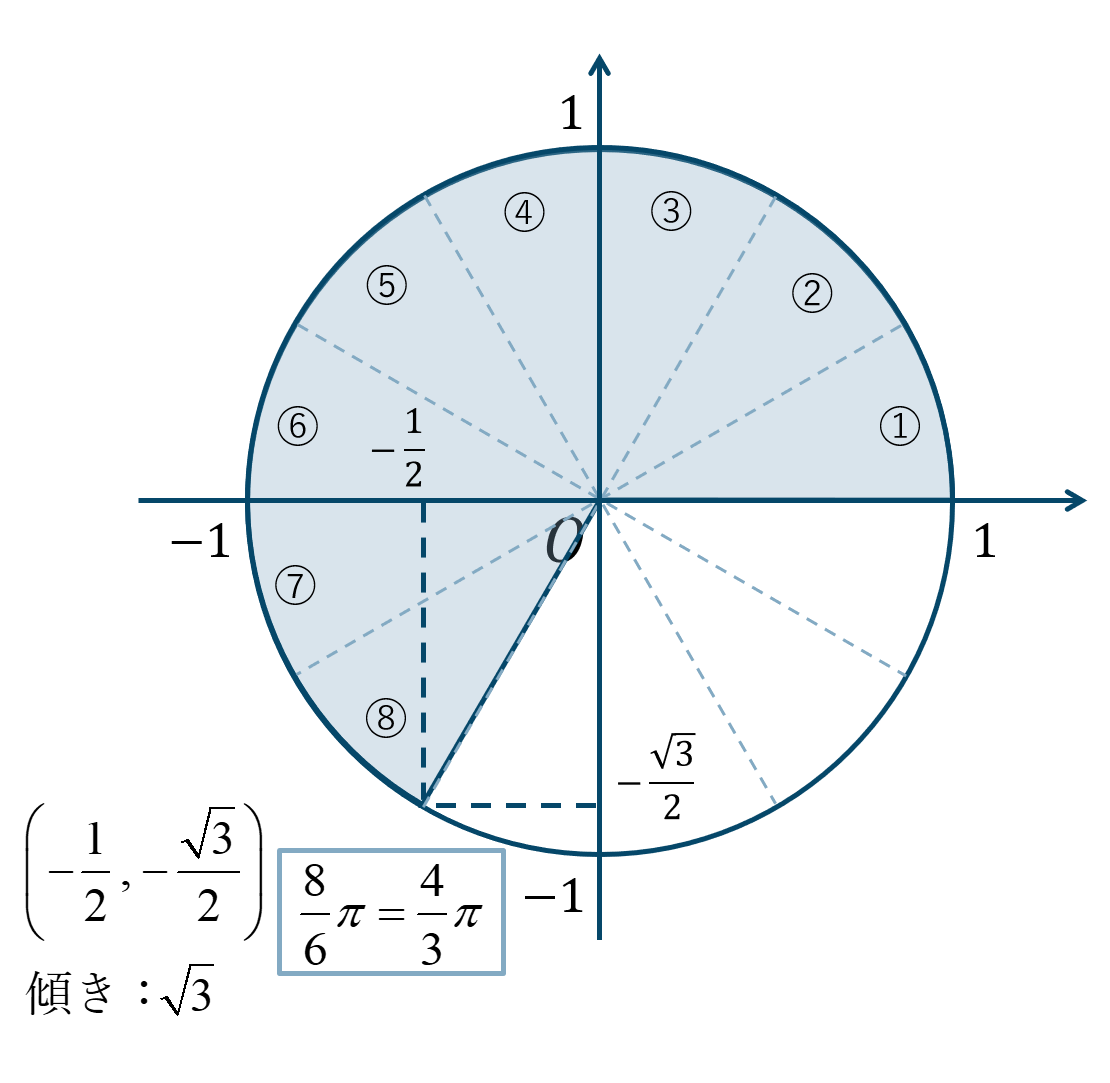
この表より、$\sin{\theta}$ は $y$ 座標の値より、$$~~~\sin{\frac{4}{3}\pi}=-\frac{\sqrt{3}}{2}$$$\cos{\theta}$ は $x$ 座標の値より、$$~~~\cos{\frac{4}{3}\pi}=-\frac{1}{2}$$$\tan{\theta}$ はこの原点と結んだ直線の傾きより、$$~~~\tan{\frac{4}{3}\pi}=\sqrt{3}$$となります。
それぞれの値については、練習を繰り返して覚えていきましょう。上下左右の対称性を利用すれば覚える量は少なくて済みます。

問題解説：三角関数の値（単位円）

問題解説(1)

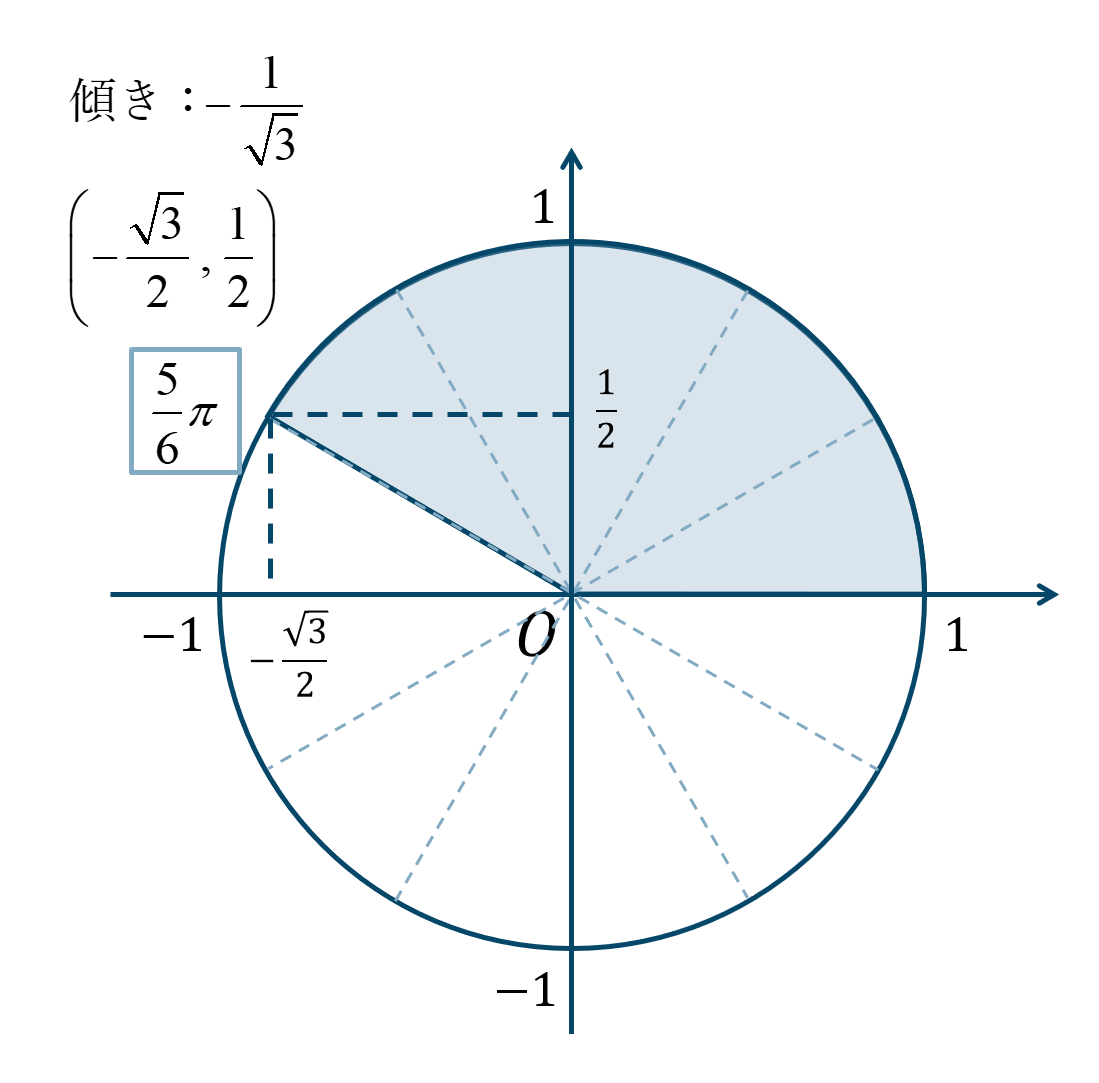
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (1)}~\frac{5}{6}\pi$$

${\Large \frac{5}{6}}\pi$ は ${\Large \frac{\pi}{6}}$ が５個分と考えて、単位円上の位置は次のようになります。

よって、答えは、$$~~~\sin{\frac{5}{6}\pi}=\frac{1}{2}$$$$~~~\cos{\frac{5}{6}\pi}=-\frac{\sqrt{3}}{2}$$$$~~~\tan{\frac{5}{6}\pi}=-\frac{1}{\sqrt{3}}$$となります。

問題解説(2)

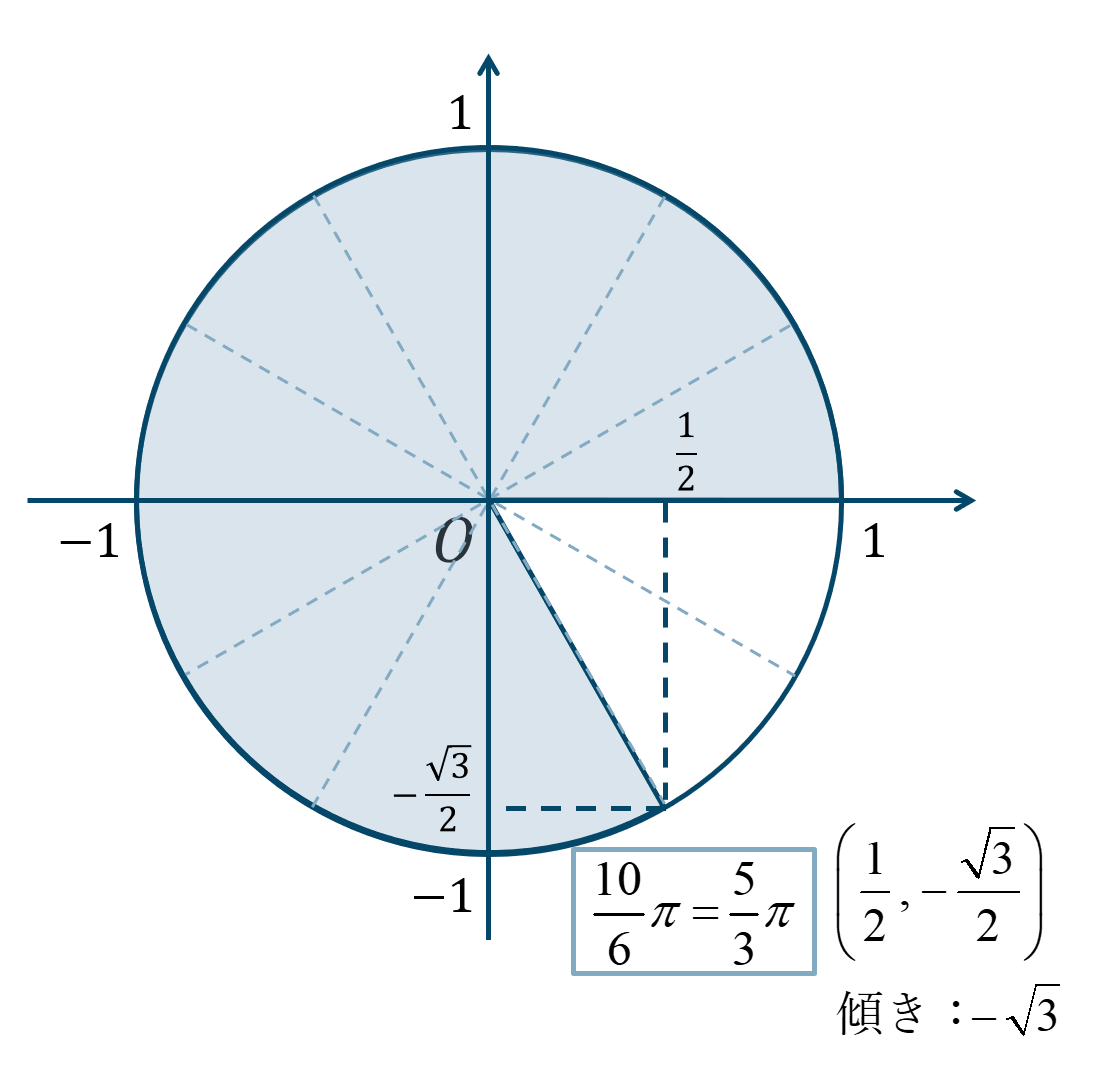
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (2)}~\frac{5}{3}\pi$$

${\Large \frac{5}{3}}\pi={\Large \frac{10}{6}}\pi$ より ${\Large \frac{\pi}{6}}$ が10個分と考えて、単位円上の位置は次のようになります。

よって、答えは、$$~~~\sin{\frac{5}{3}\pi}=-\frac{\sqrt{3}}{2}$$$$~~~\cos{\frac{5}{3}\pi}=\frac{1}{2}$$$$~~~\tan{\frac{5}{3}\pi}=-\sqrt{3}$$となります。

問題解説(3)

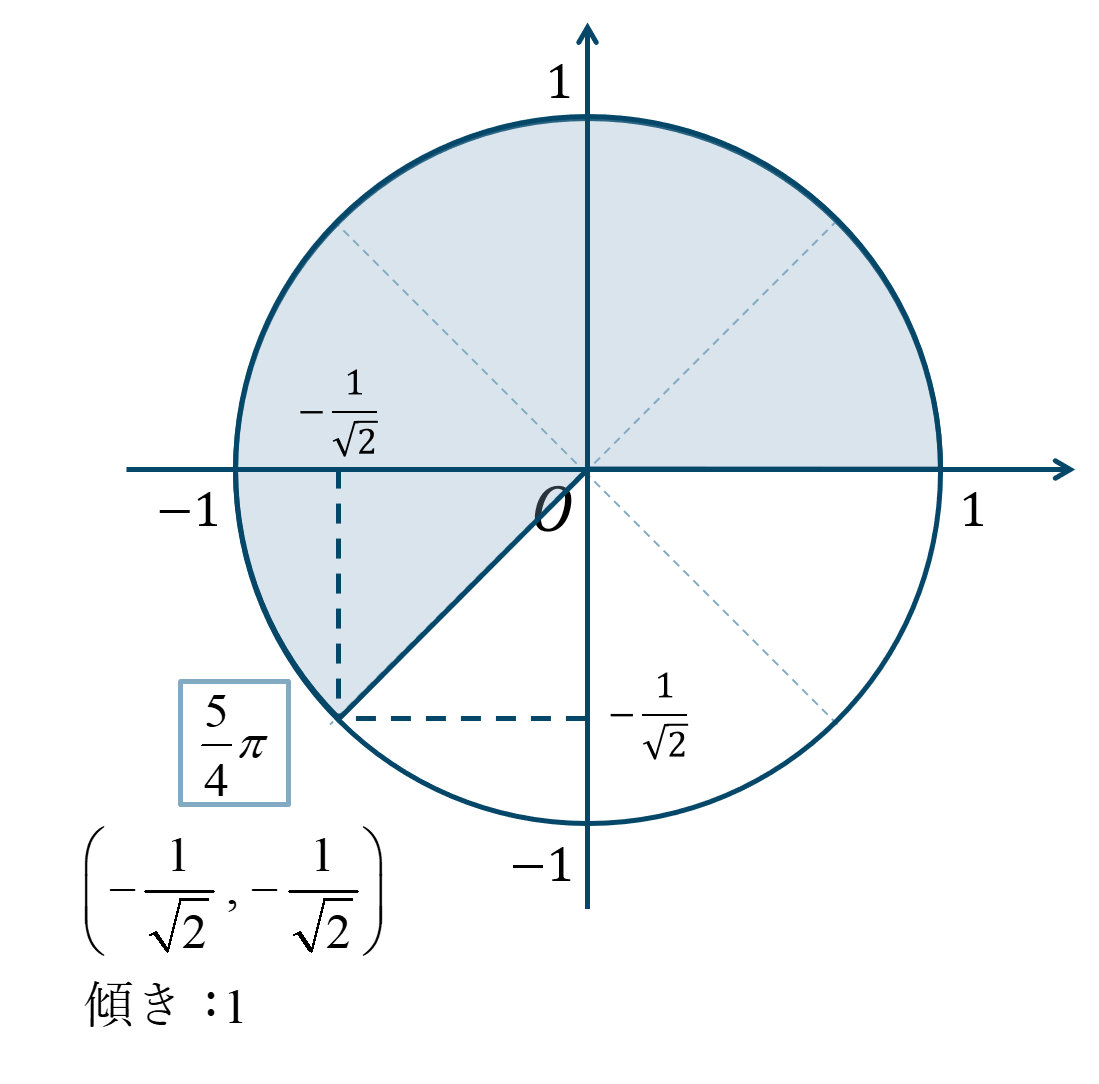
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (3)}~\frac{5}{4}\pi$$

${\Large \frac{5}{4}}\pi$ は ${\Large \frac{\pi}{4}}$ が５個分と考えて、単位円上の位置は次のようになります。

よって、答えは、$$~~~\sin{\frac{5}{4}\pi}=-\frac{1}{\sqrt{2}}$$$$~~~\cos{\frac{5}{4}\pi}=-\frac{1}{\sqrt{2}}$$$$~~~\tan{\frac{5}{4}\pi}=1$$となります。

問題解説(4)

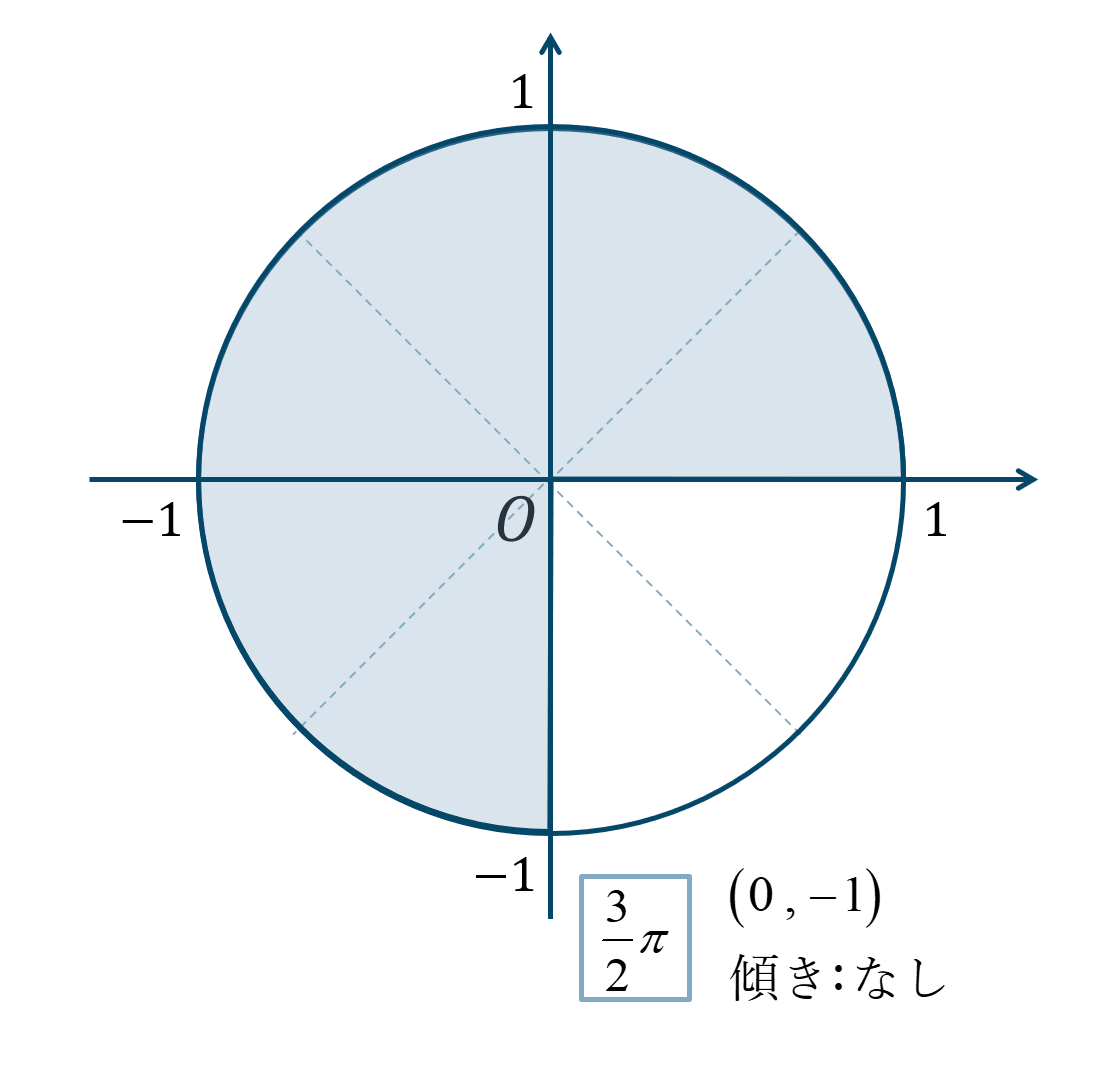
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (4)}~\frac{3}{2}\pi$$

${\Large \frac{3}{2}}\pi$ は単位円上で次のような位置になります。

よって、答えは、$$~~~\sin{\frac{3}{2}\pi}=-1$$$$~~~\cos{\frac{3}{2}\pi}=0$$また、$\tan{{\Large \frac{3}{2}}\pi}$ の解はなしとなります。

問題解説(5)

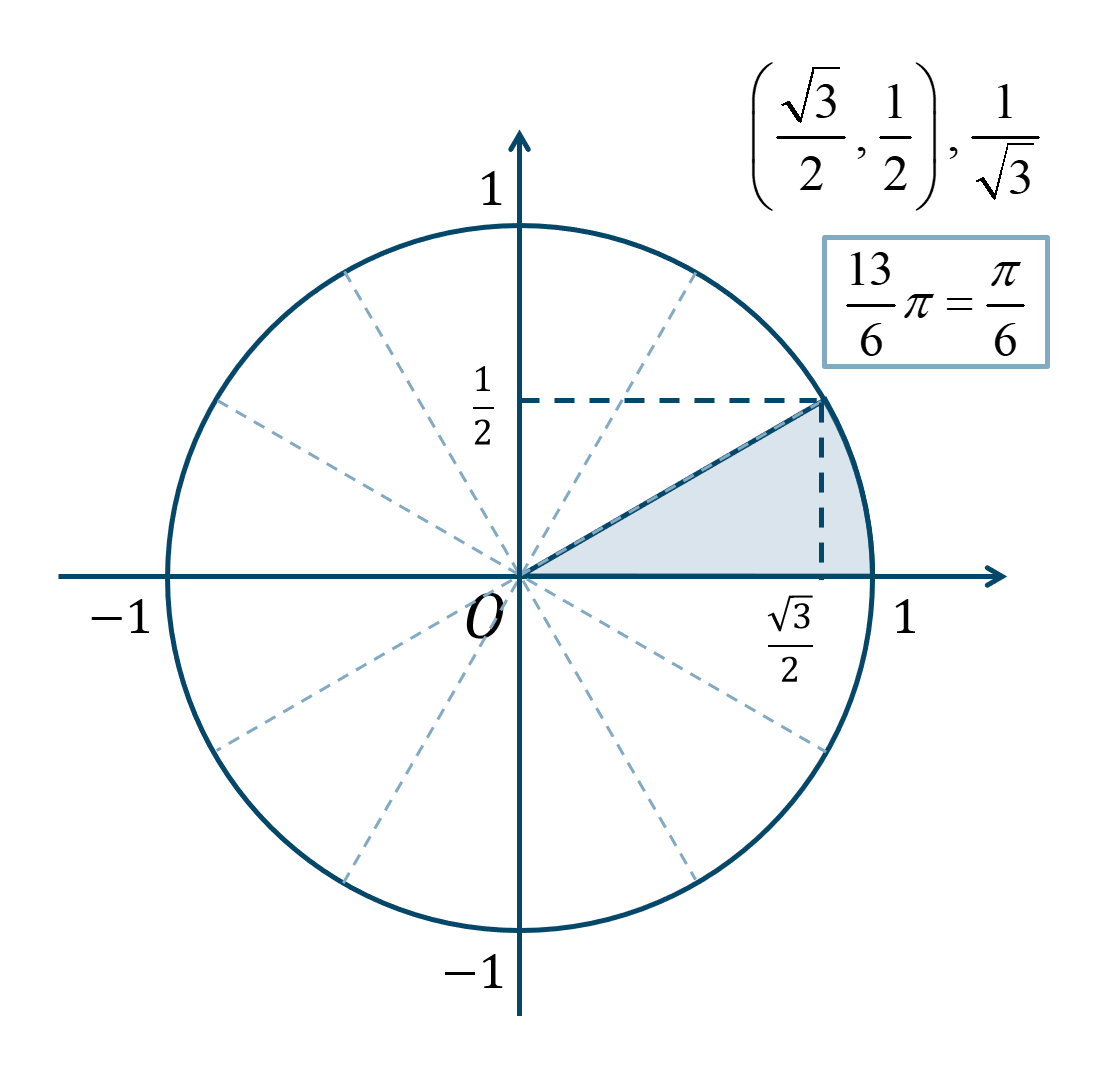
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (5)}~\frac{13}{6}\pi$$

単位円一周とさらに ${\Large \frac{\pi}{6}}$ が1個分と考えると、単位円上の位置は次のようになります。

よって、答えは、$$~~~\sin{\frac{13}{6}\pi}=\frac{1}{2}$$$$~~~\cos{\frac{13}{6}\pi}=\frac{\sqrt{3}}{2}$$$$~~~\tan{\frac{13}{6}\pi}=\frac{1}{\sqrt{3}}$$となります。

問題解説(6)

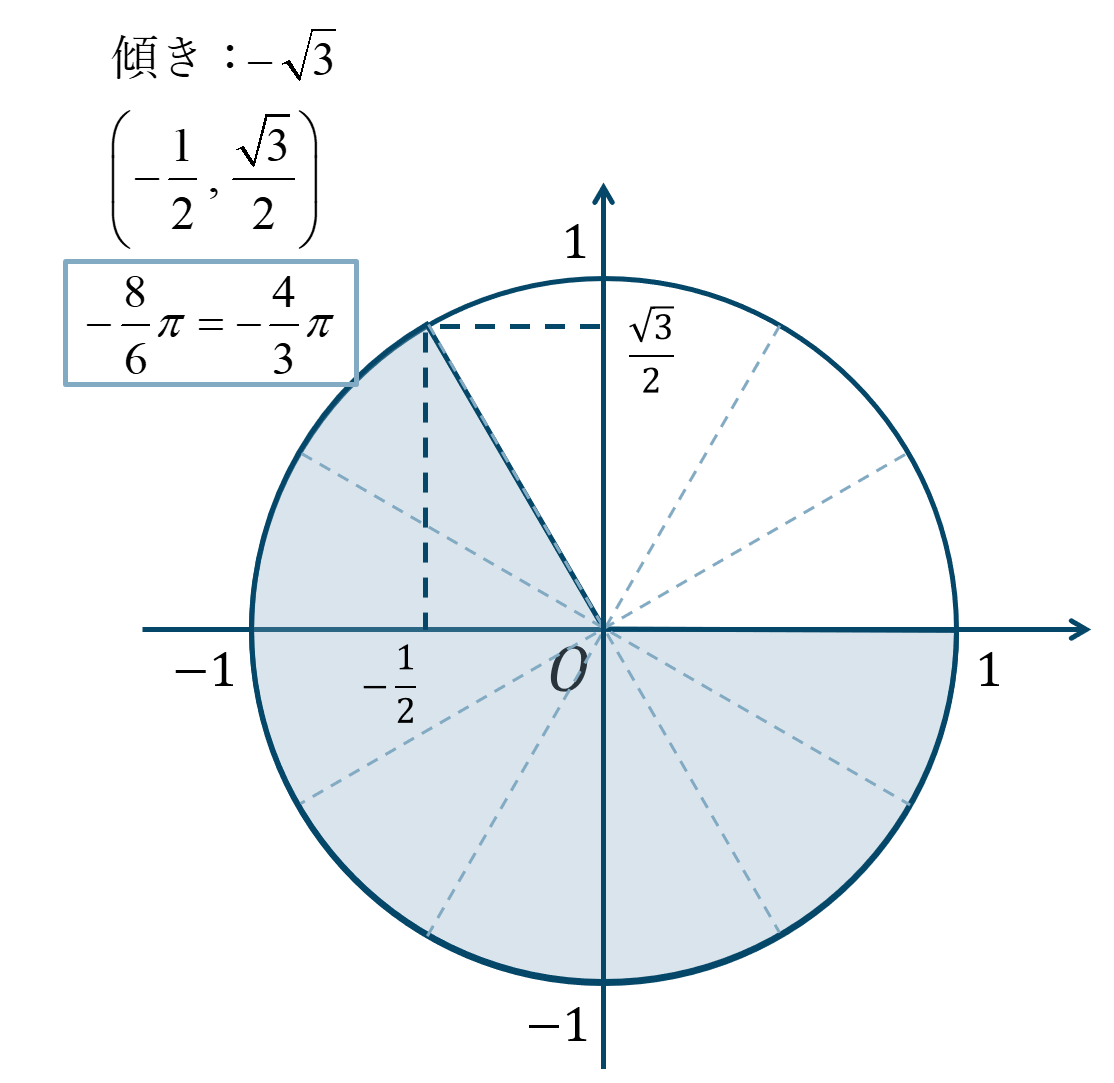
問題$\theta$ が次の角のとき、$\sin{\theta}$ $,$ $\cos{\theta}$ $,$ $\tan{\theta}$ の値を求めよ。$${\small (6)}~-\frac{4}{3}\pi$$

$-{\Large \frac{4}{3}}\pi=-{\Large \frac{8}{6}}\pi$ となるので、${\Large \frac{\pi}{6}}$ が逆向きで８個分と考えると、単位円上の位置は次のようになります。

よって、答えは、$$~~~\sin{\left(-\frac{4}{3}\pi\right)}=\frac{\sqrt{3}}{2}$$$$~~~\cos{\left(-\frac{4}{3}\pi\right)}=-\frac{1}{2}$$$$~~~\tan{\left(-\frac{4}{3}\pi\right)}=-\sqrt{3}$$となります。