三角関数の値の演習ページとなります。求め方や詳しい解説はこちらを確認してください↓

単位円と三角関数の値
原点と点 \(P\) を結んだ直線の傾きが \(\tan{\theta}\) となります。
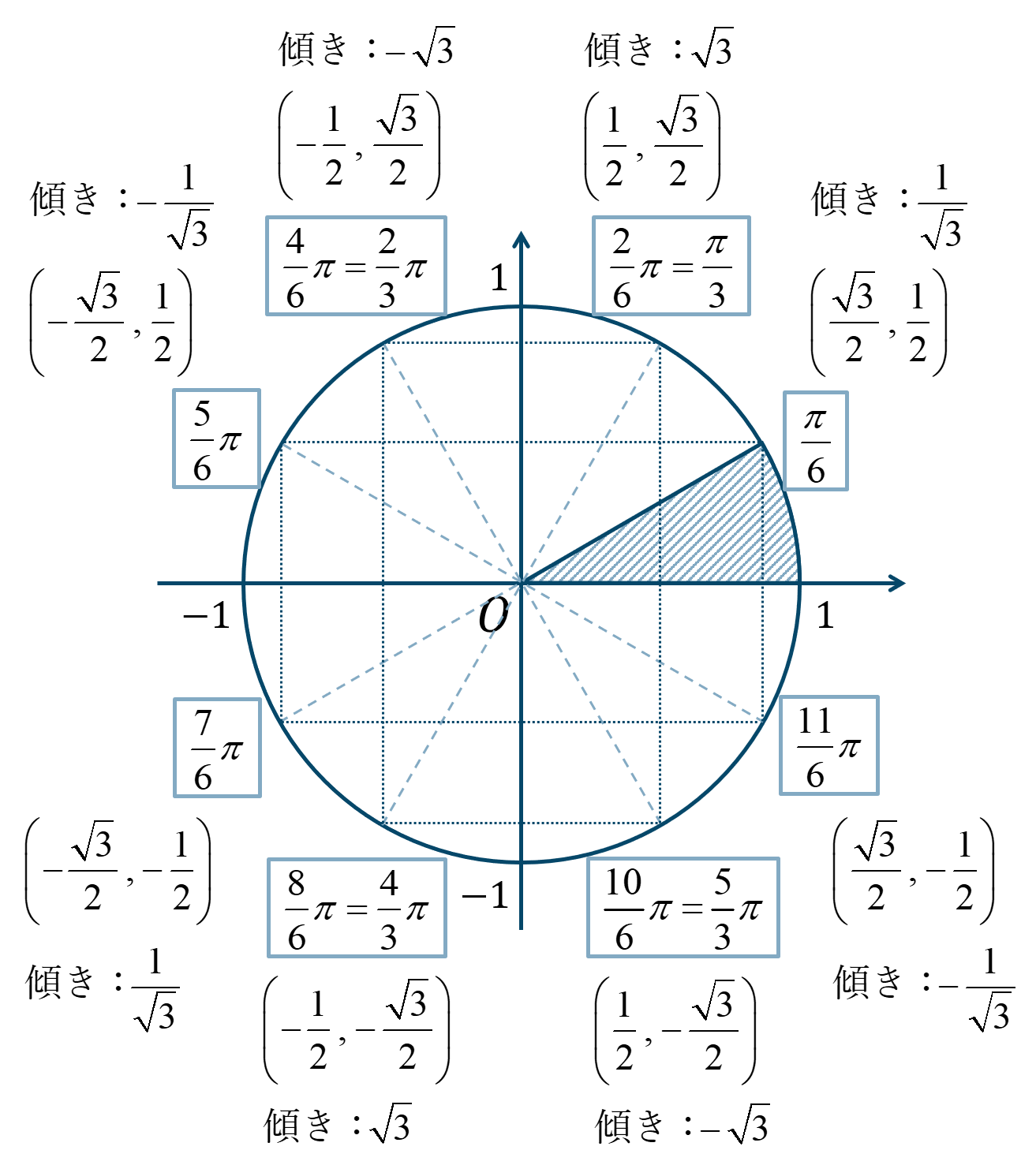
・ \({\Large \frac{\pi}{6}}\) の倍数の角
与えられた角を \({\Large \frac{\pi}{6}}\) の何個分かを考えて、単位円上の位置を確認します。

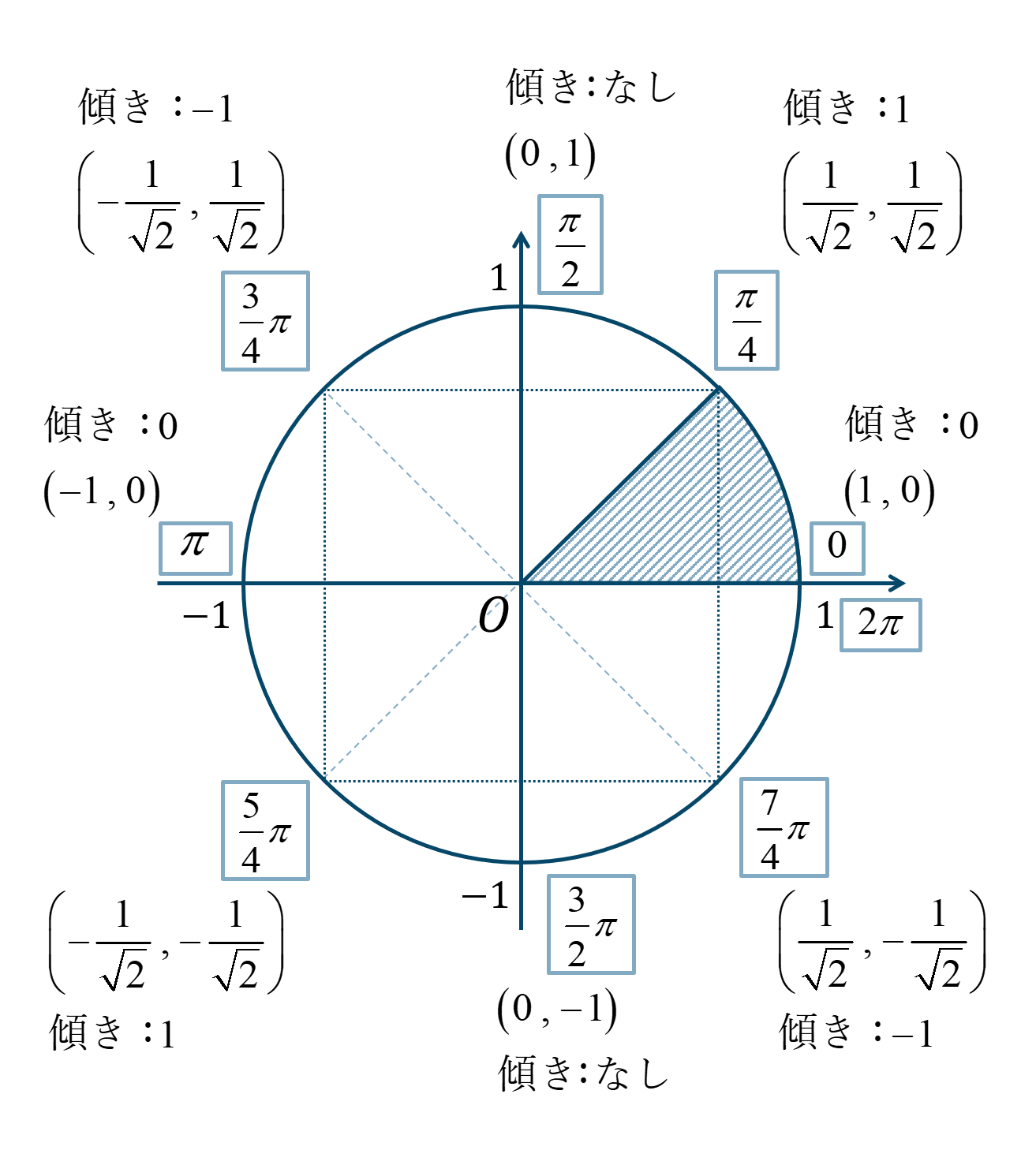
・ \({\Large \frac{\pi}{4}}\) の倍数の角
与えられた角を \({\Large \frac{\pi}{4}}\) の何個分かを考えて、単位円上の位置を確認します。

問題演習:三角関数の値(単位円)
[ 解答を見る ]
\({\Large \frac{\pi}{6}}\) が7個分と考えると、単位円上の位置は次のようになります。
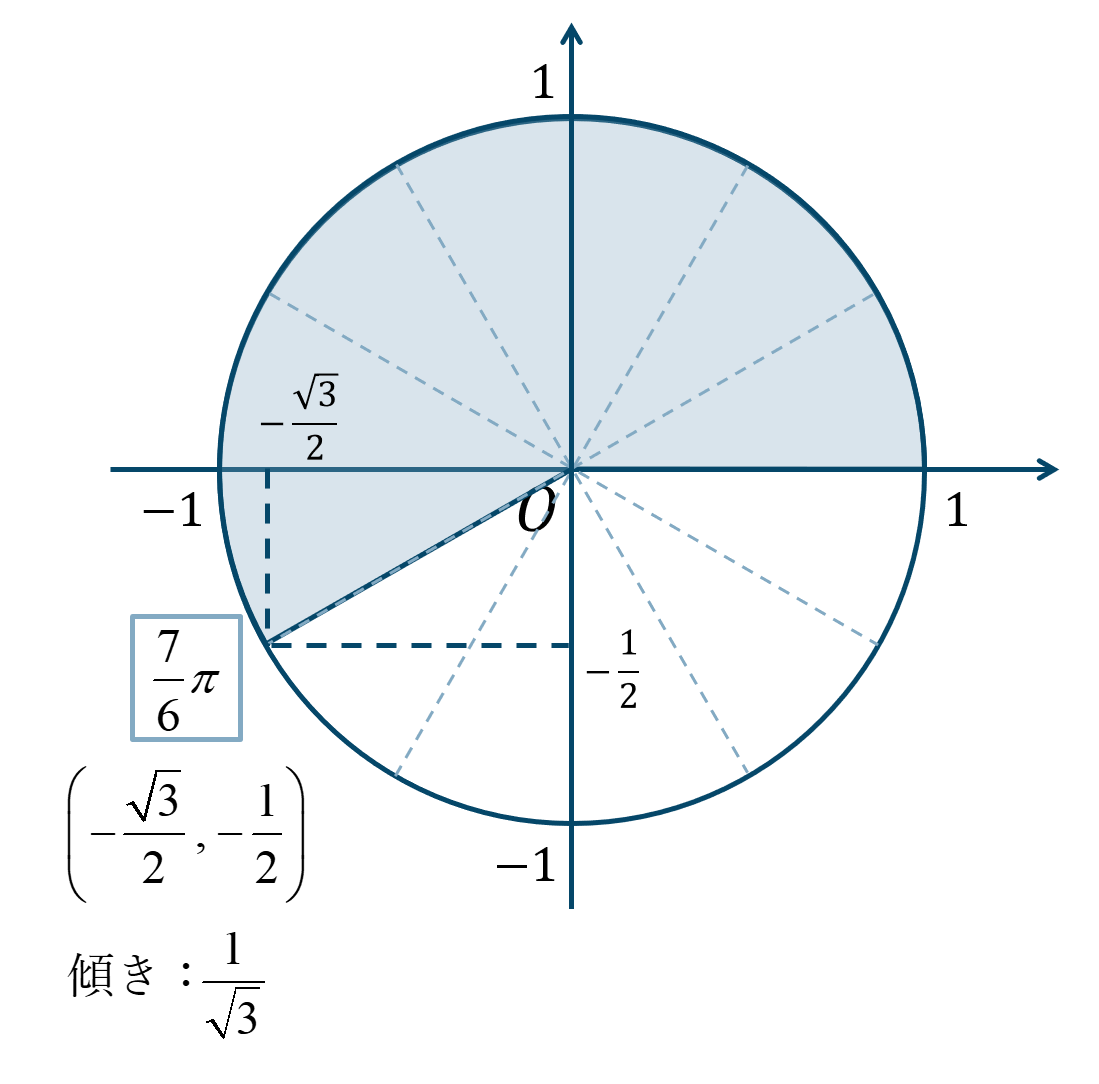
よって、答えは$$~~~\sin{\theta}=-\frac{1}{2}$$$$~~~\cos{\theta}=-\frac{\sqrt{3}}{2}$$$$~~~\tan{\theta}=\frac{1}{\sqrt{3}}$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{3}}={\Large \frac{2}{6}}\pi\) となり、\({\Large \frac{\pi}{6}}\) が2個分と考えると、単位円上の位置は次のようになります。
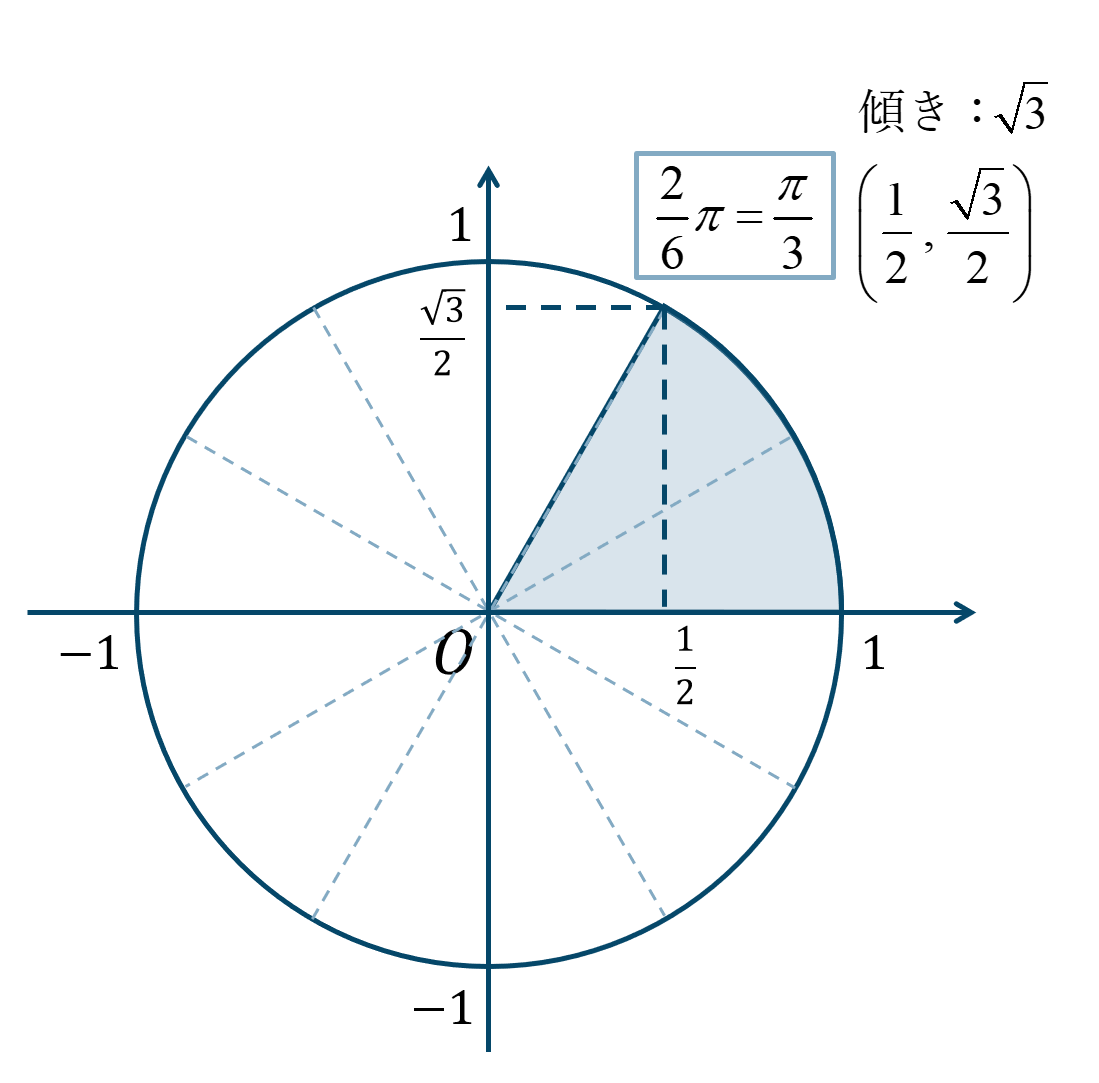
よって、答えは$$~~~\sin{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=\frac{1}{2}$$$$~~~\tan{\theta}=\sqrt{3}$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{4}}\) が3個分と考えると、単位円上の位置は次のようになります。
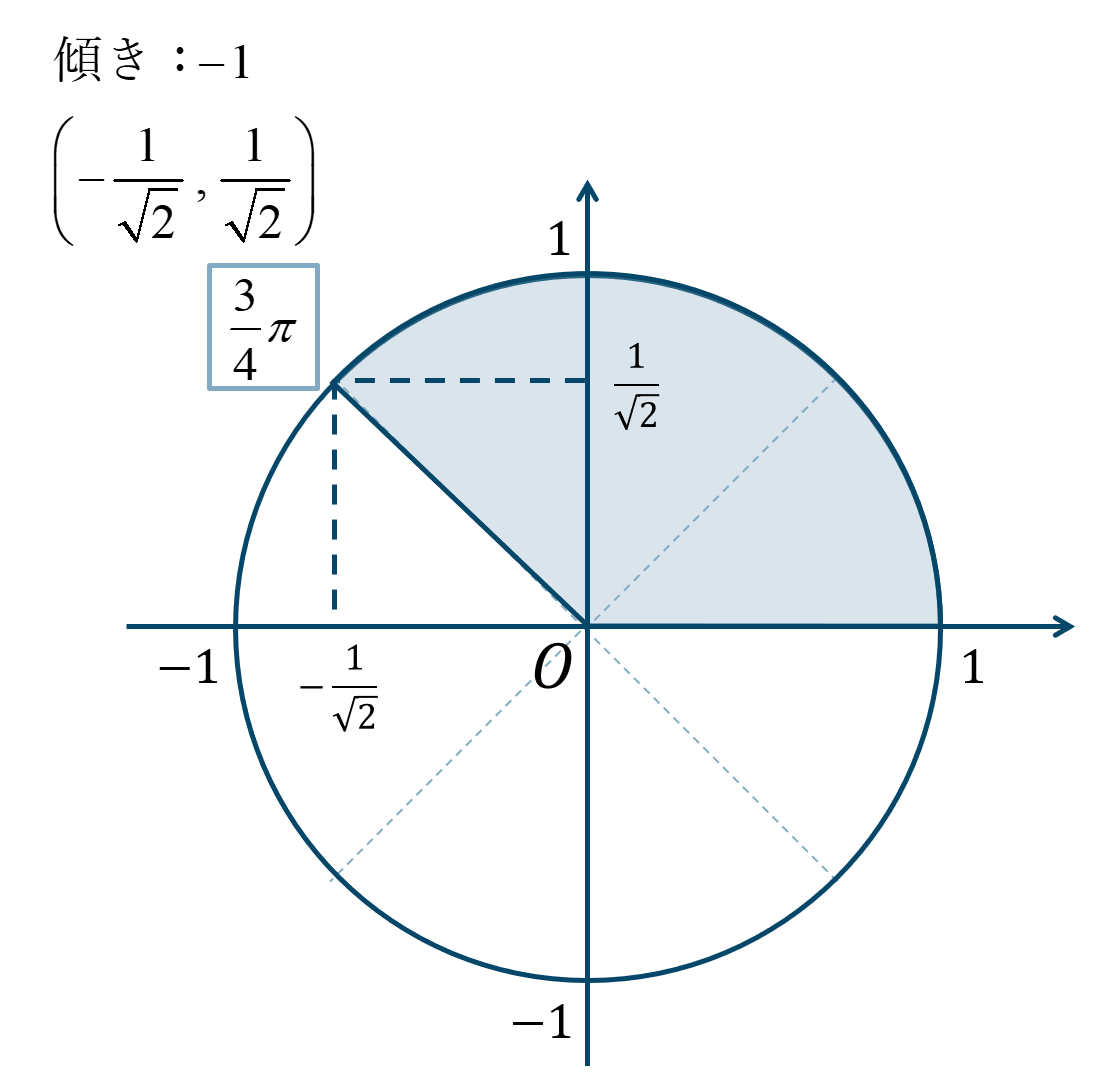
よって、答えは$$~~~\sin{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\cos{\theta}=-\frac{1}{\sqrt{2}}$$$$~~~\tan{\theta}=-1$$となります。
[ 解答を見る ]
\(\theta=\pi\) の単位円上の位置は次のようになります。
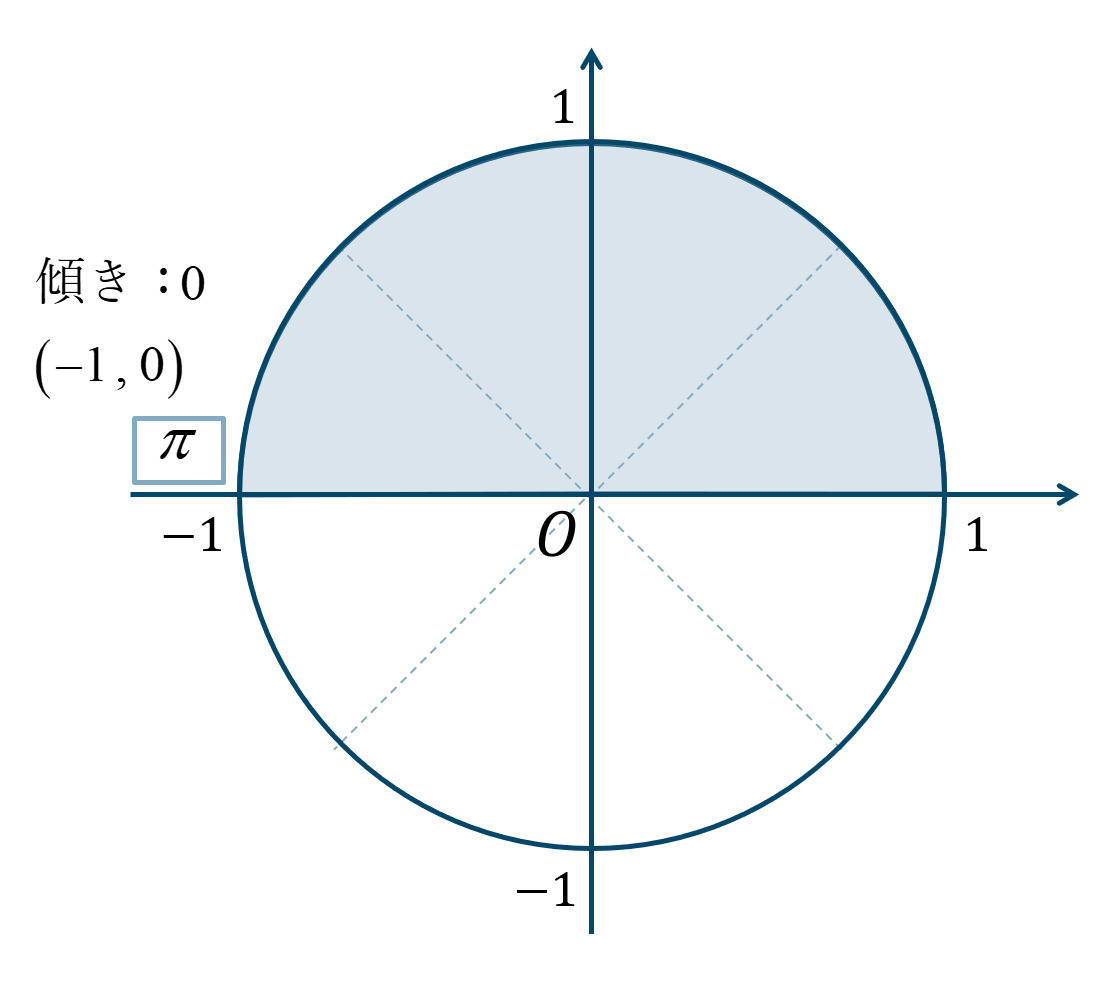
よって、答えは$$~~~\sin{\theta}=0$$$$~~~\cos{\theta}=-1$$$$~~~\tan{\theta}=0$$となります。
[ 解答を見る ]
\({\Large \frac{2}{3}}\pi={\Large \frac{4}{6}}\pi\) となり、\({\Large \frac{\pi}{6}}\) が4個分と考えると、単位円上の位置は次のようになります。
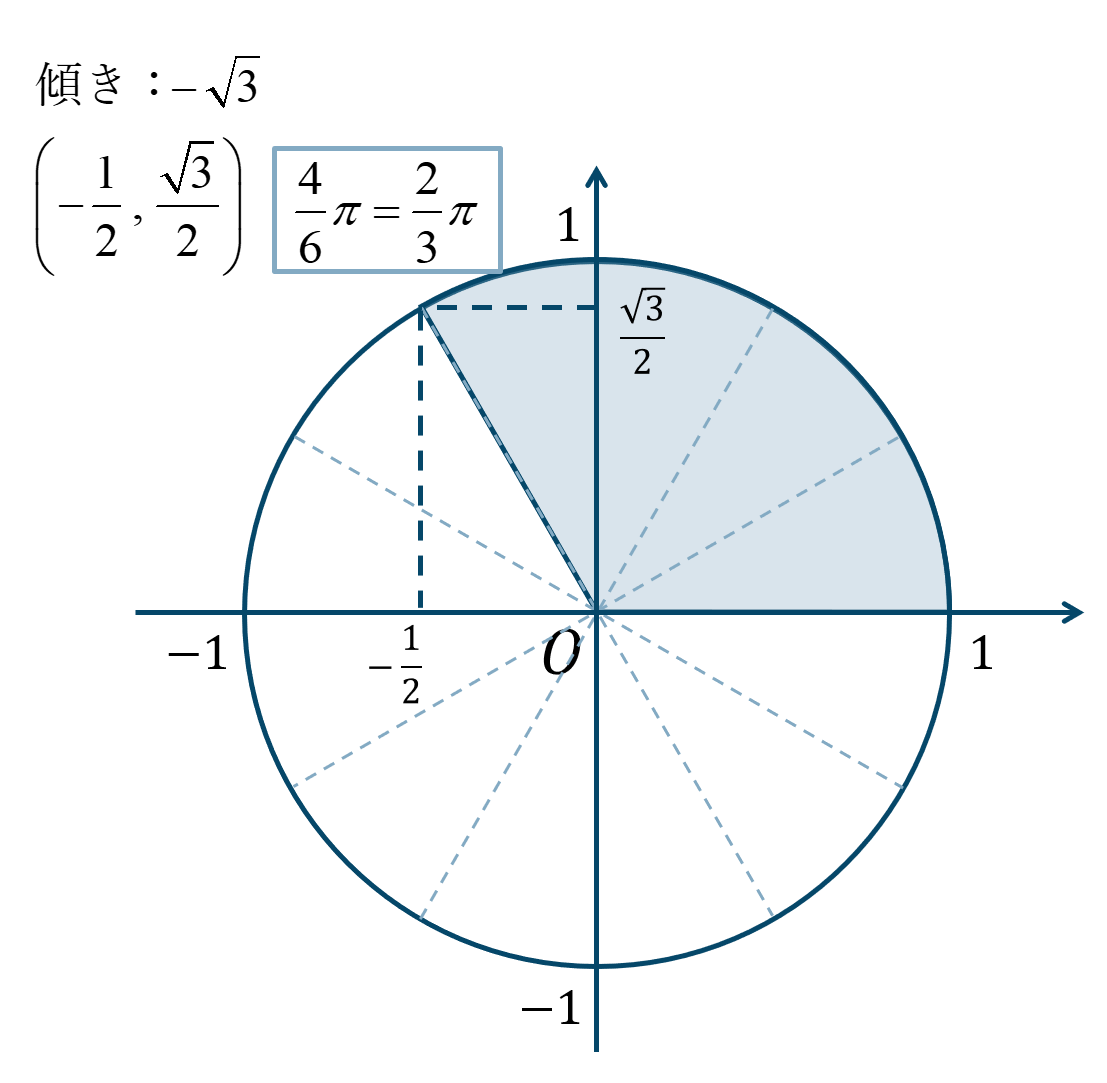
よって、答えは$$~~~\sin{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=-\frac{1}{2}$$$$~~~\tan{\theta}=-\sqrt{3}$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{6}}\) が11個分と考えると、単位円上の位置は次のようになります。
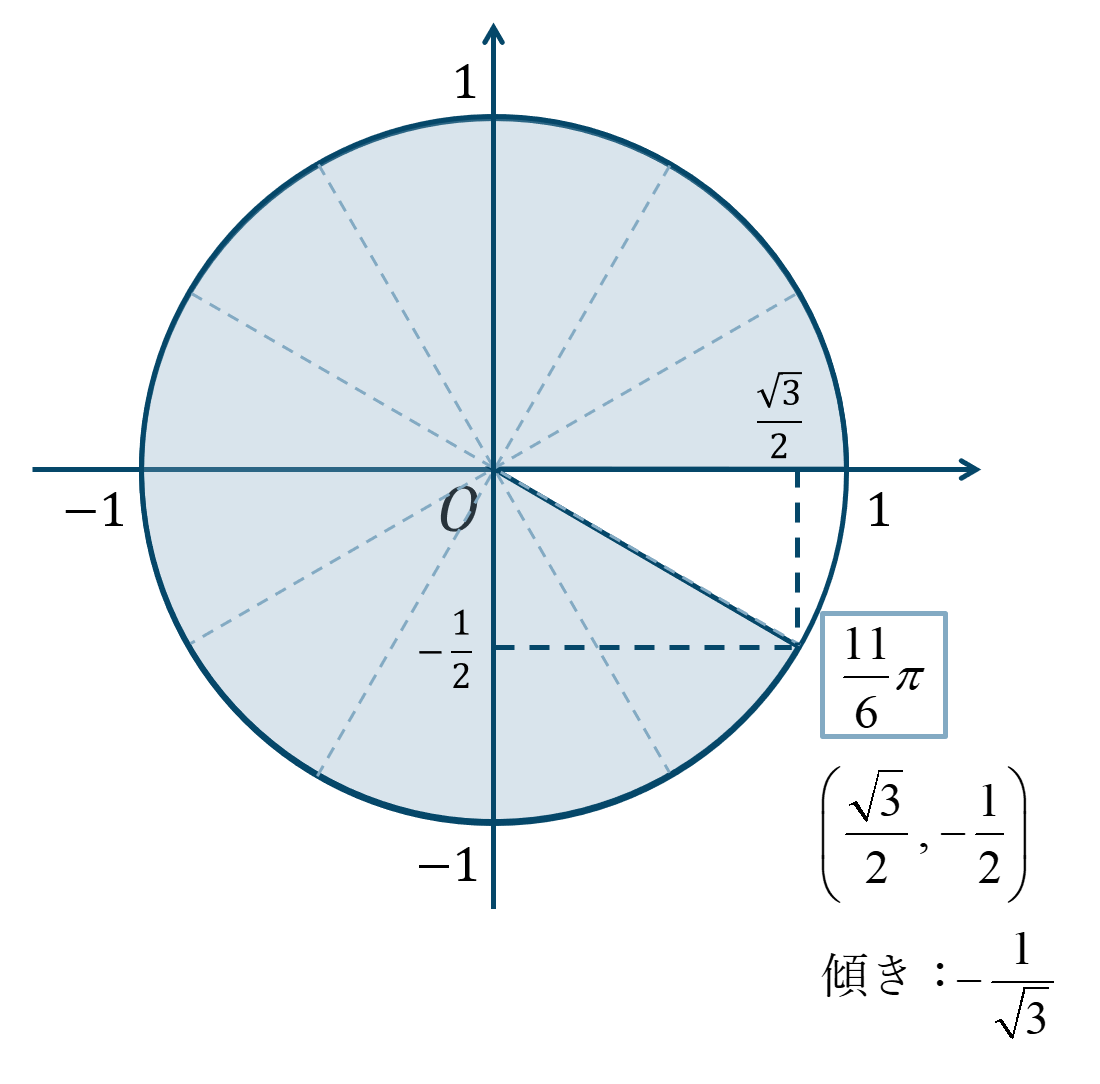
よって、答えは$$~~~\sin{\theta}=-\frac{1}{2}$$$$~~~\cos{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\tan{\theta}=-\frac{1}{\sqrt{3}}$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{4}}\) が7個分と考えると、単位円上の位置は次のようになります。
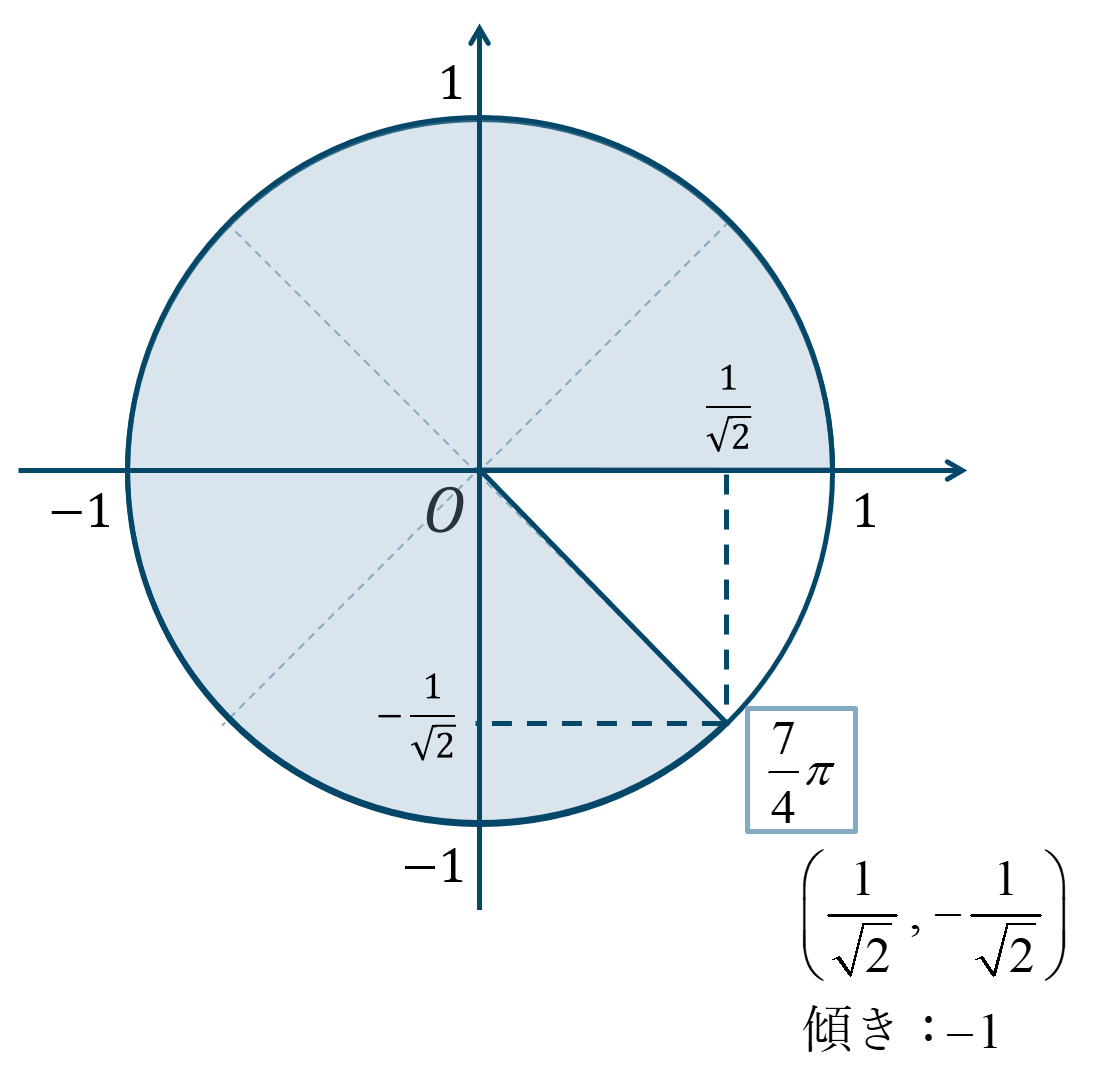
よって、答えは$$~~~\sin{\theta}=-\frac{1}{\sqrt{2}}$$$$~~~\cos{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\tan{\theta}=-1$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{4}}\) が1個分と考えると、単位円上の位置は次のようになります。
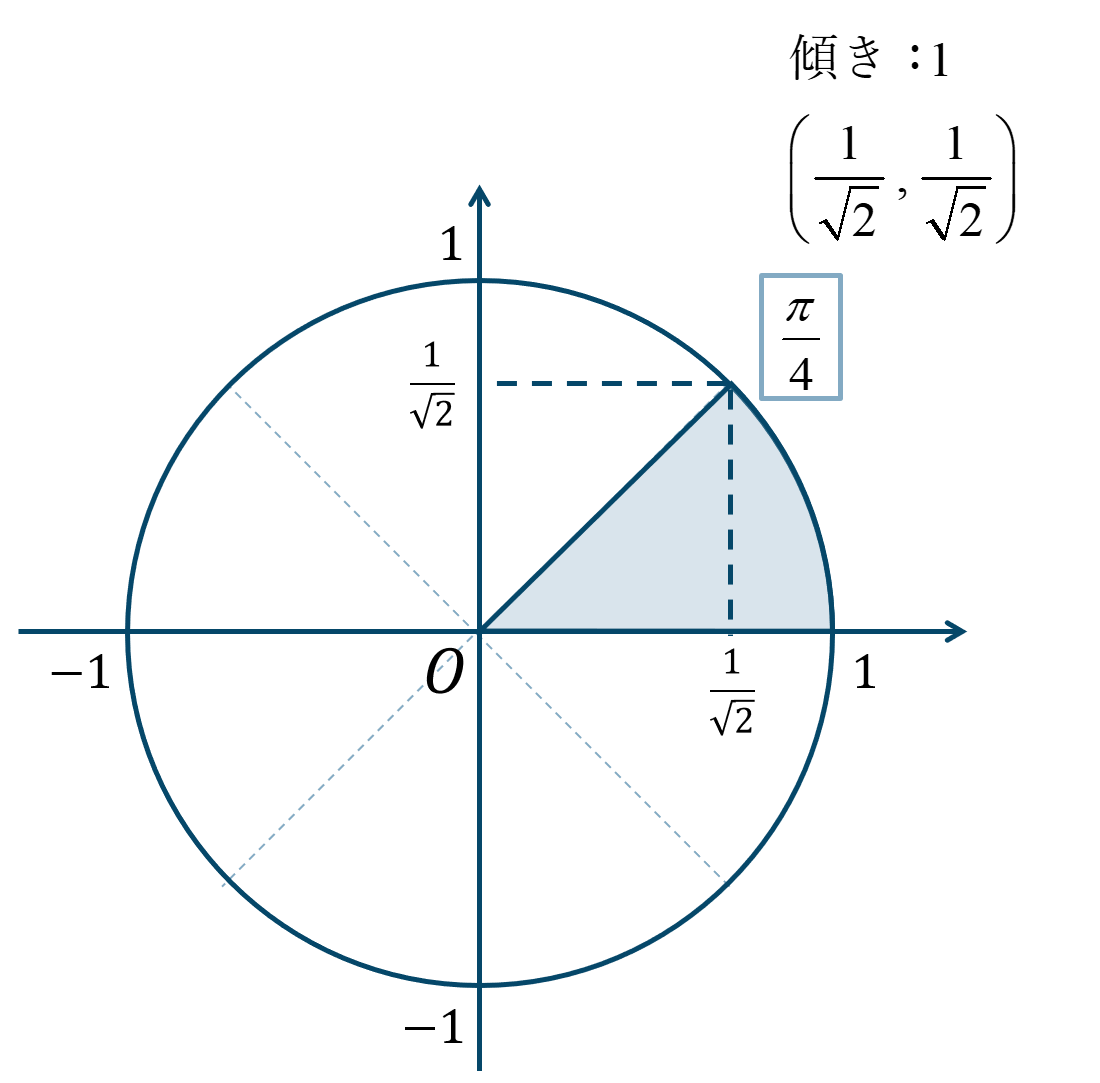
よって、答えは$$~~~\sin{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\cos{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\tan{\theta}=1$$となります。
[ 解答を見る ]
\(\theta=0\) の単位円上の位置は次のようになります。
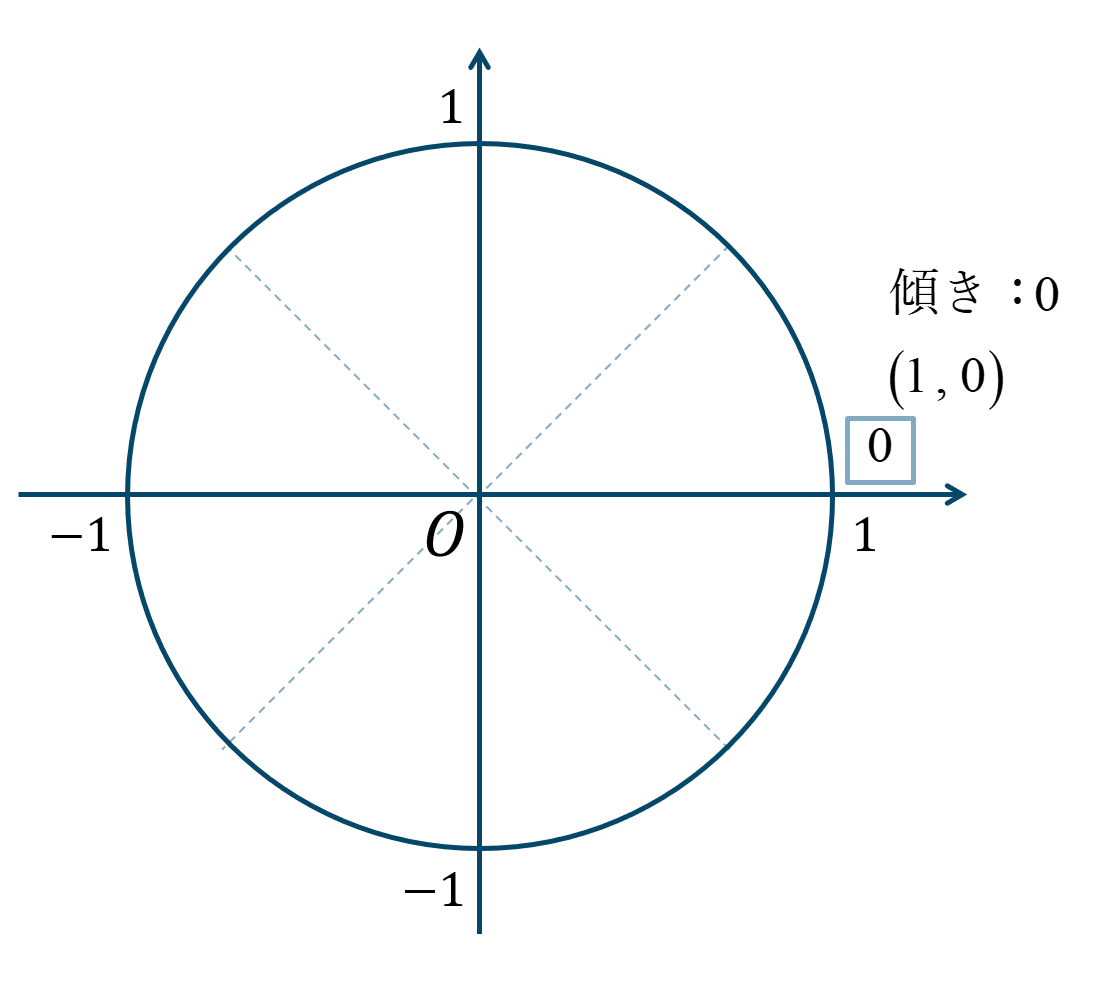
よって、答えは$$~~~\sin{\theta}=0$$$$~~~\cos{\theta}=1$$$$~~~\tan{\theta}=0$$となります。
[ 解答を見る ]
\({\Large \frac{\pi}{6}}\) が1個分と考えると、単位円上の位置は次のようになります。
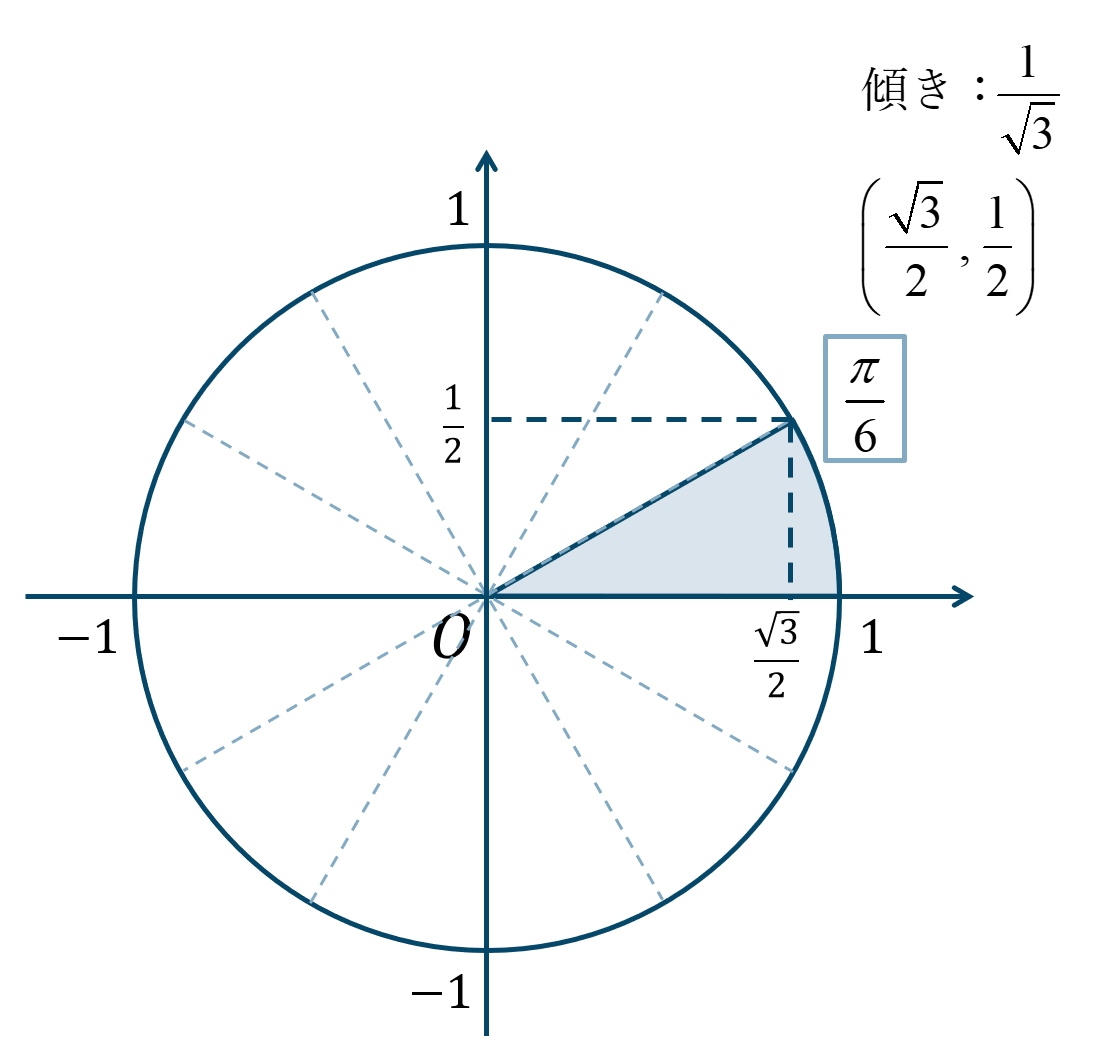
よって、答えは$$~~~\sin{\theta}=\frac{1}{2}$$$$~~~\cos{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\tan{\theta}=\frac{1}{\sqrt{3}}$$となります。
[ 解答を見る ]
\(\theta={\Large \frac{\pi}{2}}\) の単位円上の位置は次のようになります。

よって、答えは$$~~~\sin{\theta}=1$$$$~~~\cos{\theta}=0$$また、\(\tan{\theta}\) は解なしとなります。
[ 解答を見る ]
\({\Large \frac{4}{3}}\pi={\Large \frac{8}{6}}\pi\) となり、\({\Large \frac{\pi}{6}}\) が8個分と考えると、単位円上の位置は次のようになります。
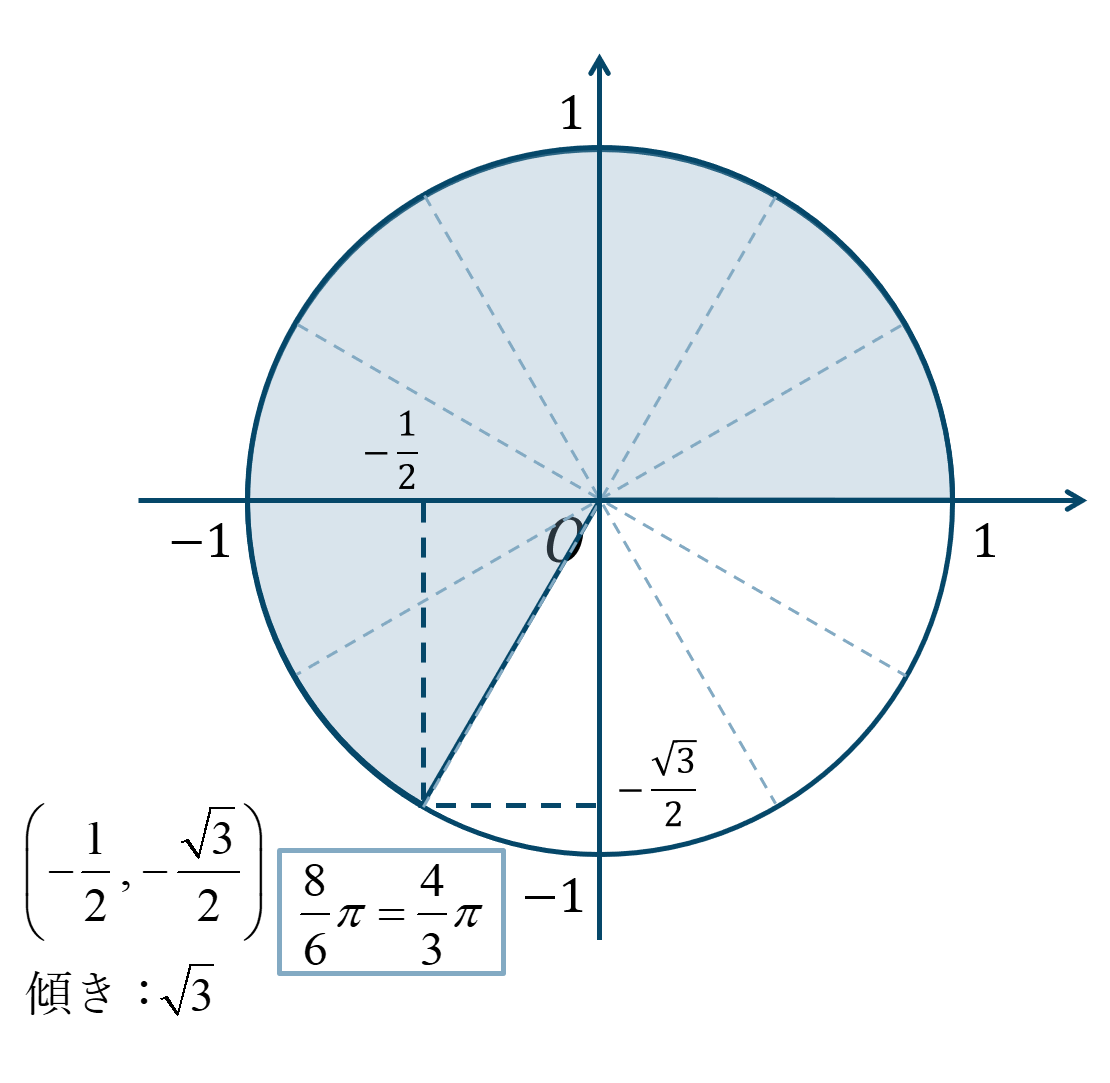
よって、答えは$$~~~\sin{\theta}=-\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=-\frac{1}{2}$$$$~~~\tan{\theta}=\sqrt{3}$$となります。
[ 解答を見る ]
逆向きに \({\Large \frac{\pi}{6}}\) が7個分と考えると、単位円上の位置は次のようになります。
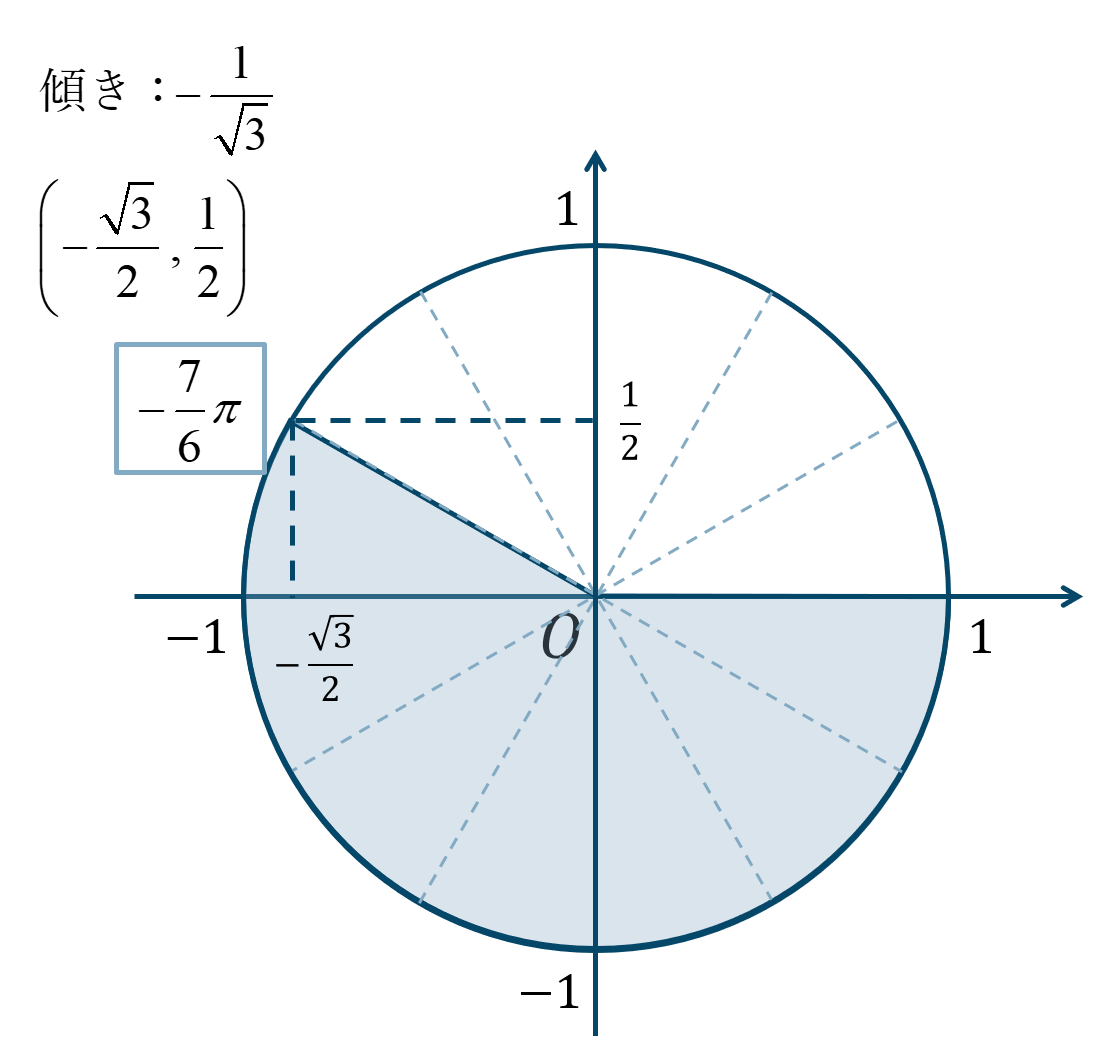
よって、答えは$$~~~\sin{\theta}=\frac{1}{2}$$$$~~~\cos{\theta}=-\frac{\sqrt{3}}{2}$$$$~~~\tan{\theta}=-\frac{1}{\sqrt{3}}$$となります。
[ 解答を見る ]
\(-{\Large \frac{\pi}{3}}=-{\Large \frac{2}{6}}\pi\) となり、逆向きに \({\Large \frac{\pi}{6}}\) が2個分と考えると、単位円上の位置は次のようになります。
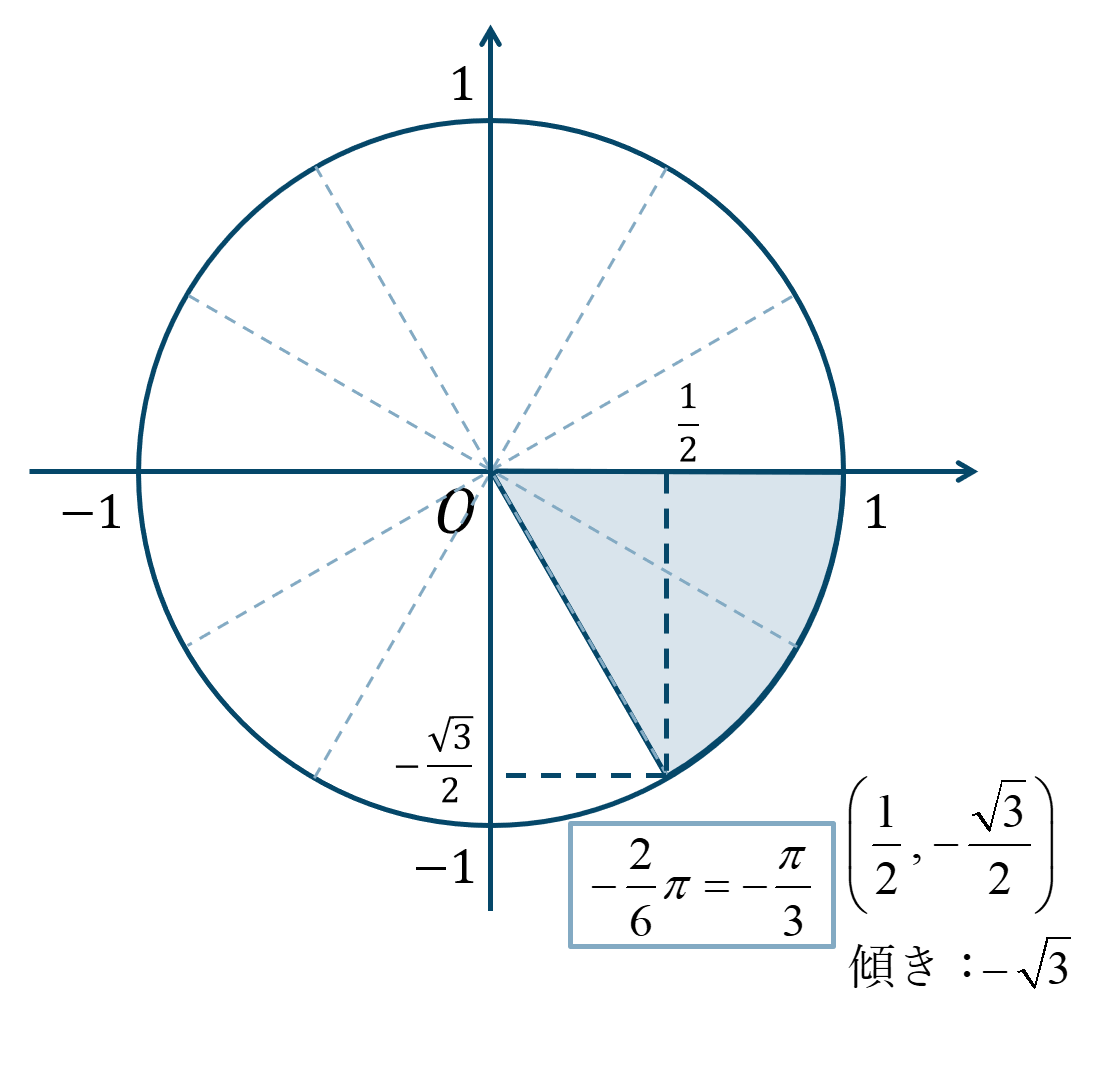
よって、答えは$$~~~\sin{\theta}=-\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=\frac{1}{2}$$$$~~~\tan{\theta}=-\sqrt{3}$$となります。
[ 解答を見る ]
逆向きに \({\Large \frac{\pi}{4}}\) が5個分と考えると、単位円上の位置は次のようになります。
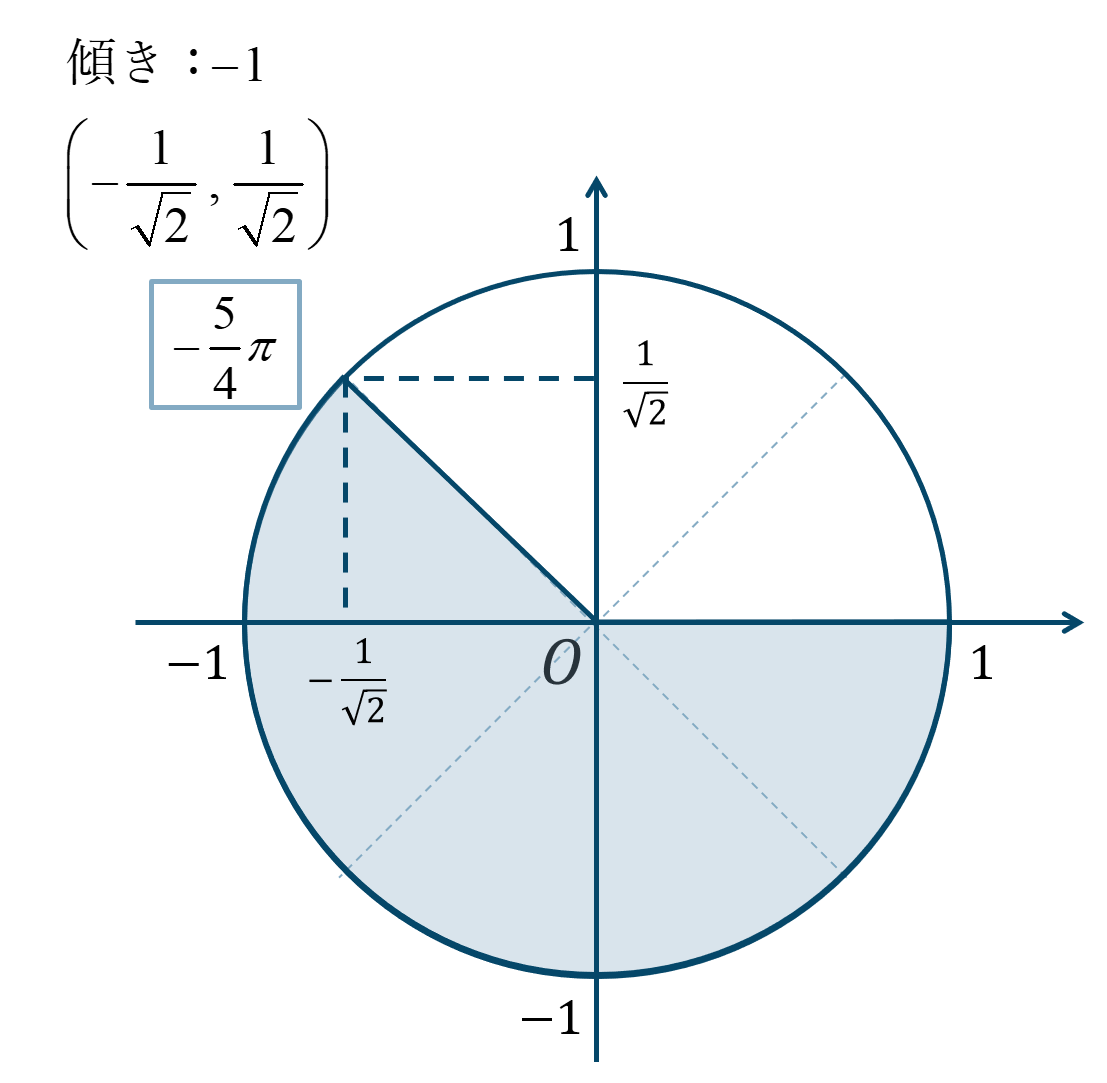
よって、答えは$$~~~\sin{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\cos{\theta}=-\frac{1}{\sqrt{2}}$$$$~~~\tan{\theta}=-1$$となります。
[ 解答を見る ]
\(-{\Large \frac{5}{3}}\pi=-{\Large \frac{10}{6}}\pi\) となり、逆向きに \({\Large \frac{\pi}{6}}\) が10個分と考えると、単位円上の位置は次のようになります。
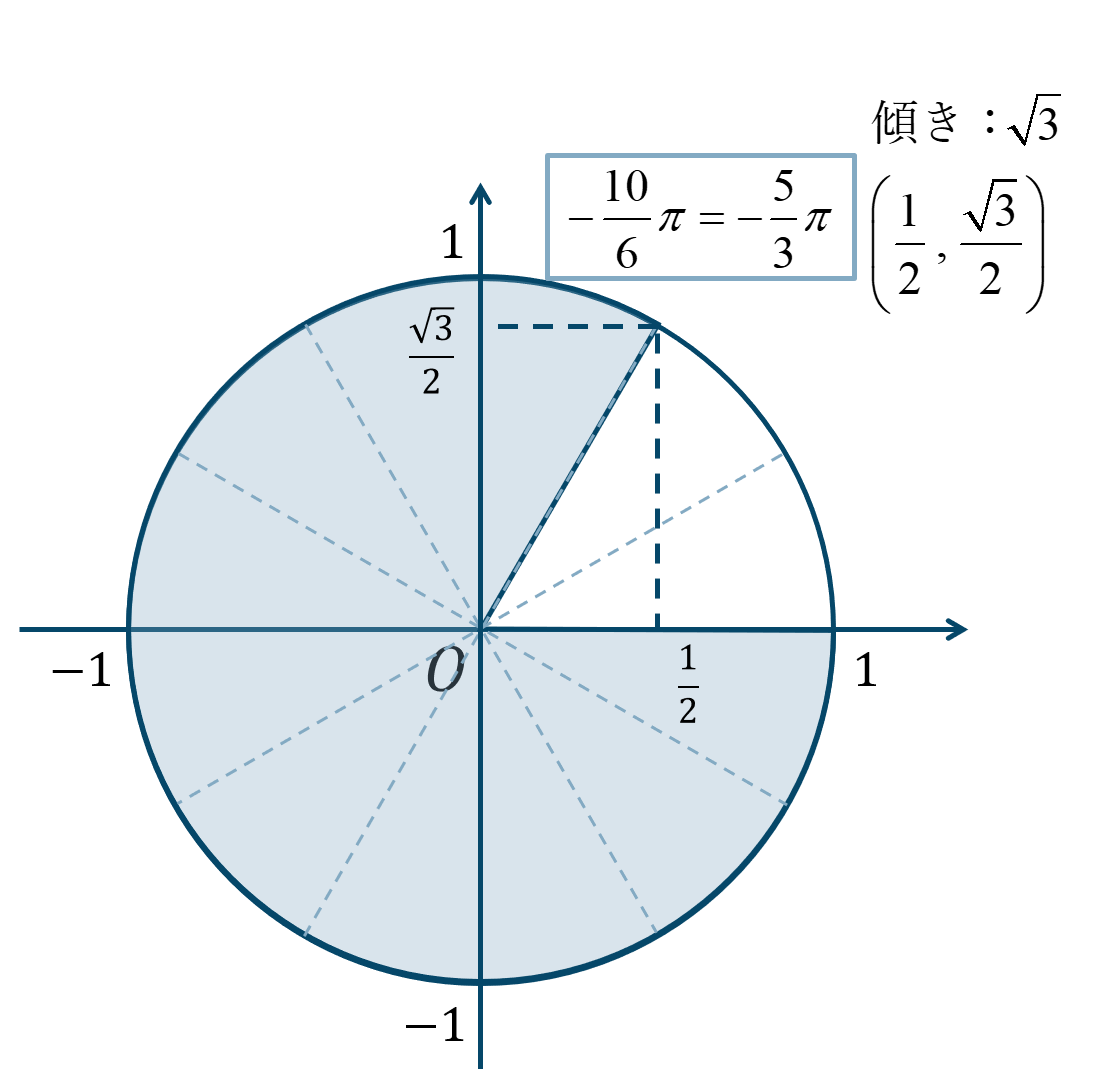
よって、答えは$$~~~\sin{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=\frac{1}{2}$$$$~~~\tan{\theta}=\sqrt{3}$$となります。
[ 解答を見る ]
単位円1周とさらに \({\Large \frac{\pi}{6}}\) が7個分と考えると、単位円上の位置は次のようになります。
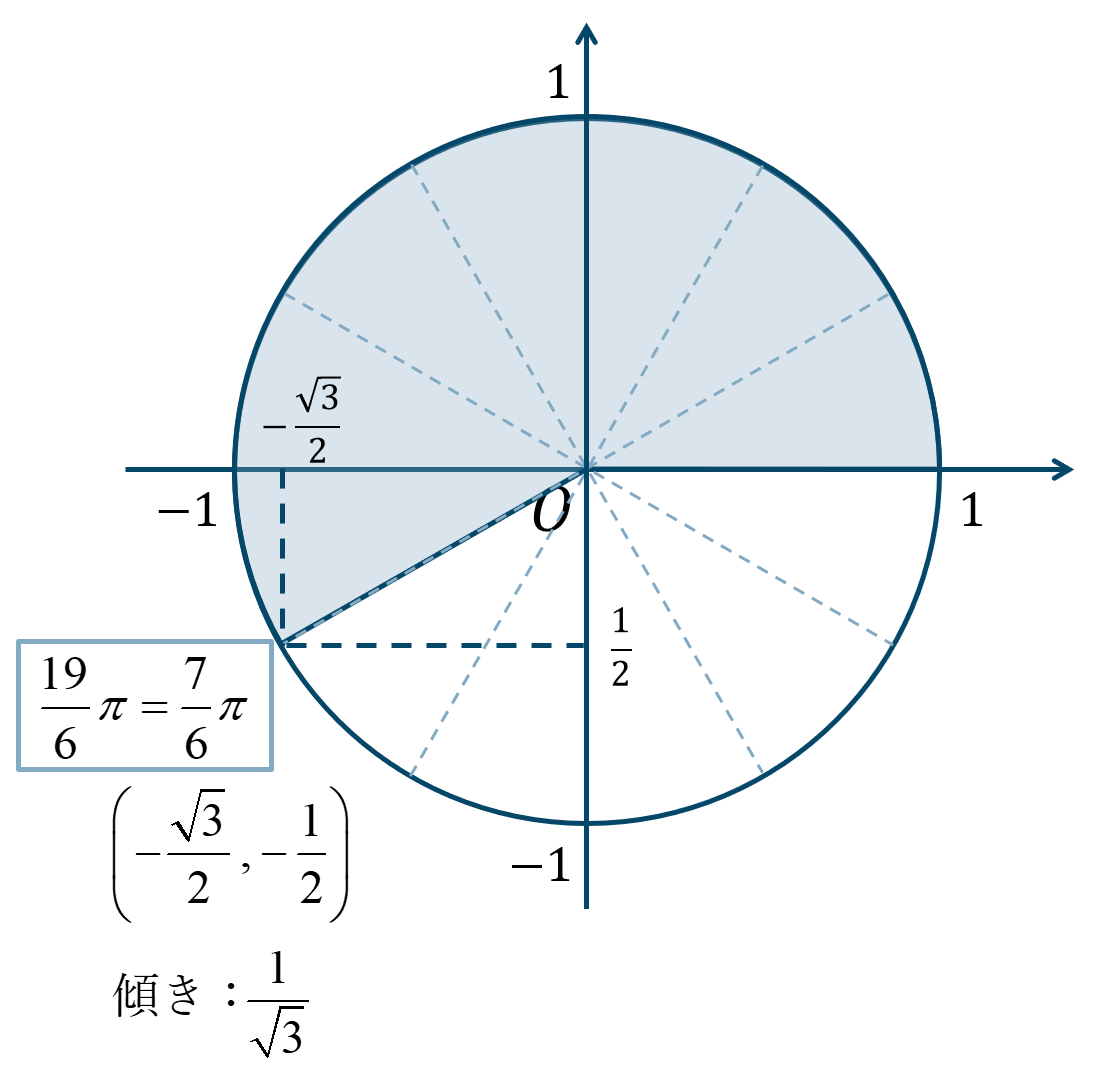
よって、答えは$$~~~\sin{\theta}=-\frac{1}{2}$$$$~~~\cos{\theta}=-\frac{\sqrt{3}}{2}$$$$~~~\tan{\theta}=\frac{1}{\sqrt{3}}$$となります。
[ 解答を見る ]
\({\Large \frac{13}{3}}\pi={\Large \frac{26}{6}}\pi\) となり、単位円2周と \({\Large \frac{\pi}{6}}\) が2個分と考えると、単位円上の位置は次のようになります。
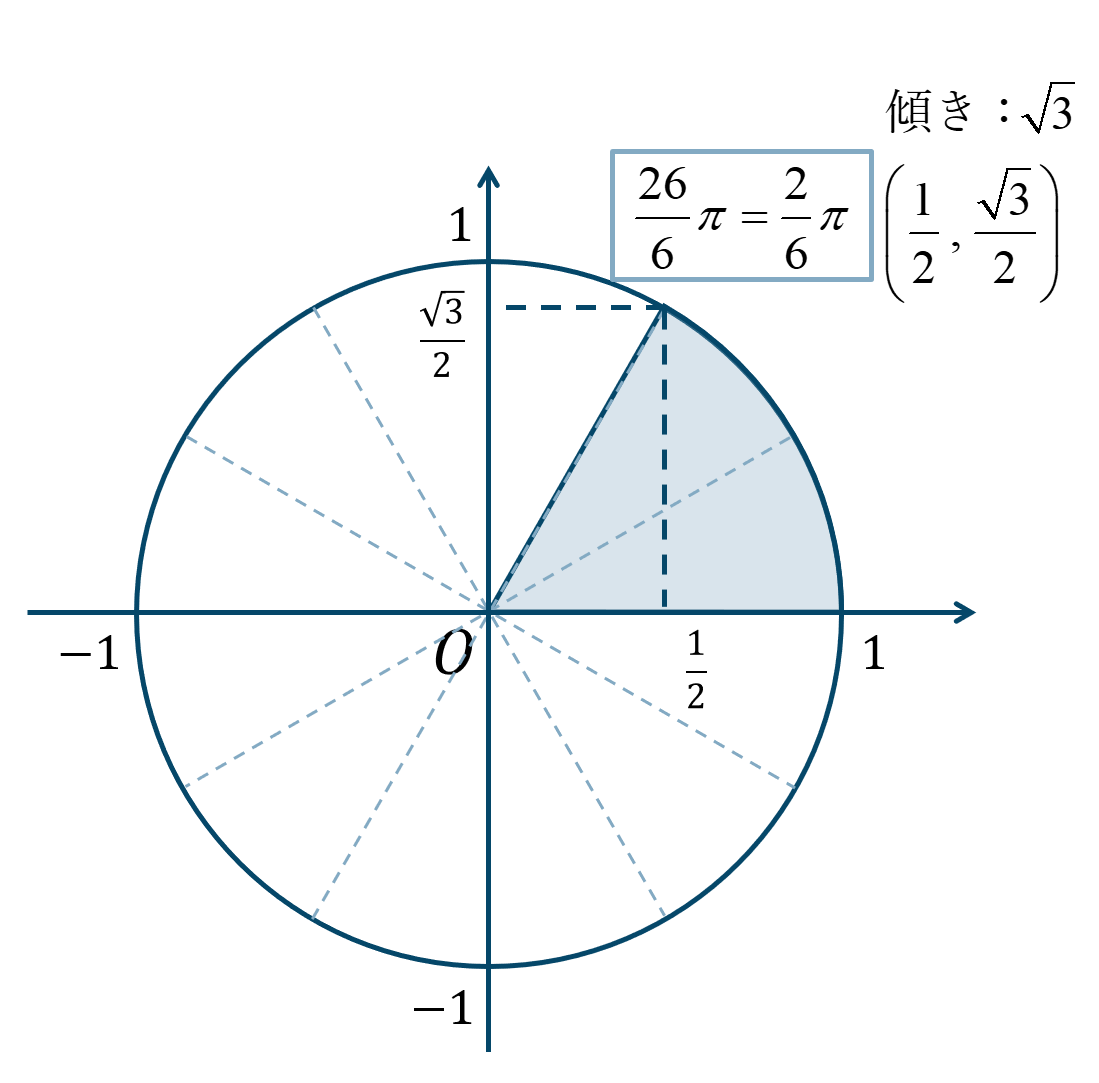
よって、答えは$$~~~\sin{\theta}=\frac{\sqrt{3}}{2}$$$$~~~\cos{\theta}=\frac{1}{2}$$$$~~~\tan{\theta}=\sqrt{3}$$となります。
[ 解答を見る ]
単位円1周と \({\Large \frac{\pi}{4}}\) が7個分と考えると、単位円上の位置は次のようになります。
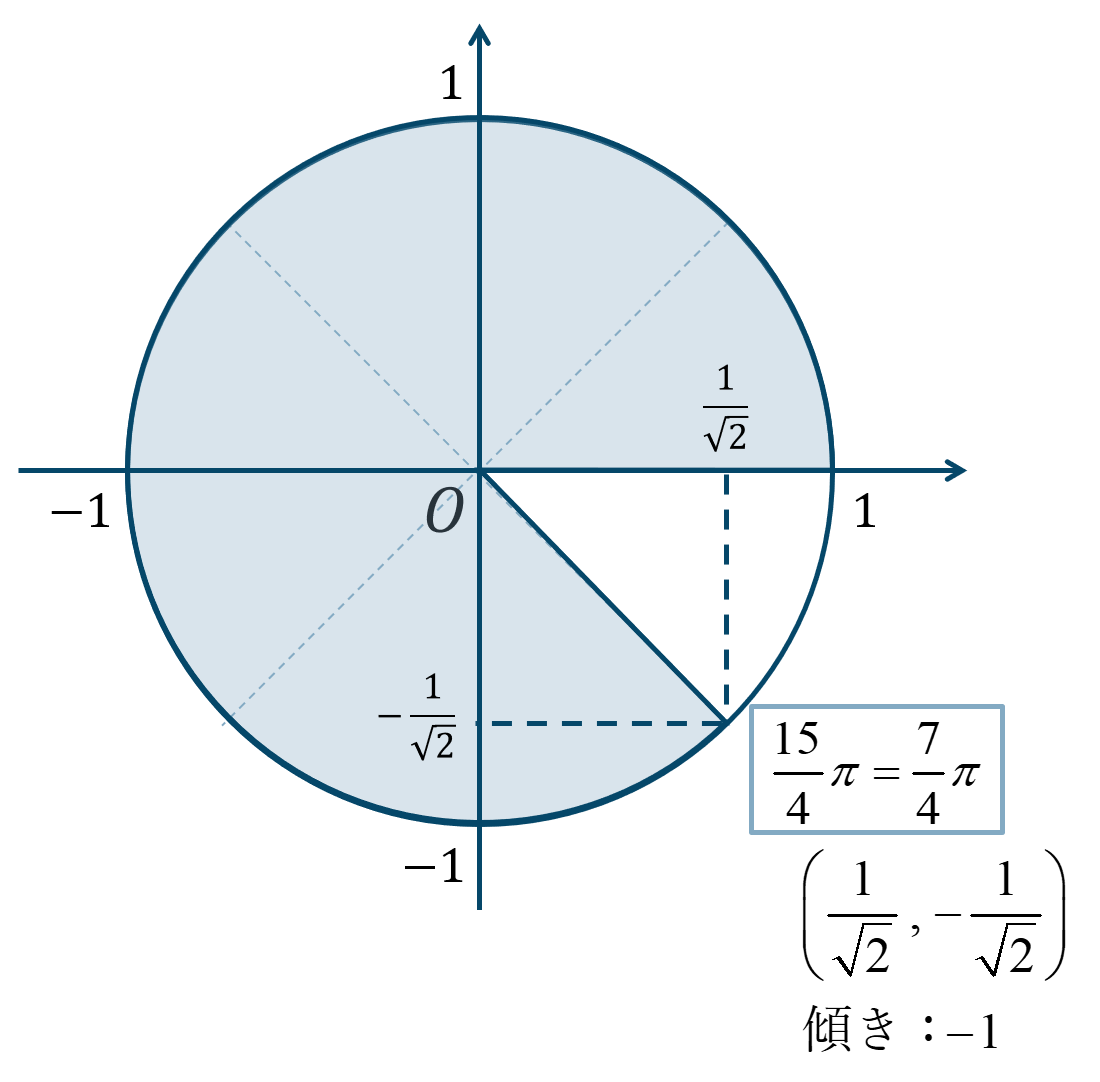
よって、答えは$$~~~\sin{\theta}=-\frac{1}{\sqrt{2}}$$$$~~~\cos{\theta}=\frac{1}{\sqrt{2}}$$$$~~~\tan{\theta}=-1$$となります。
[ 解答を見る ]
単位円1周と \({\Large \frac{\pi}{2}}\) が3個分と考えると、単位円上の位置は次のようになります。
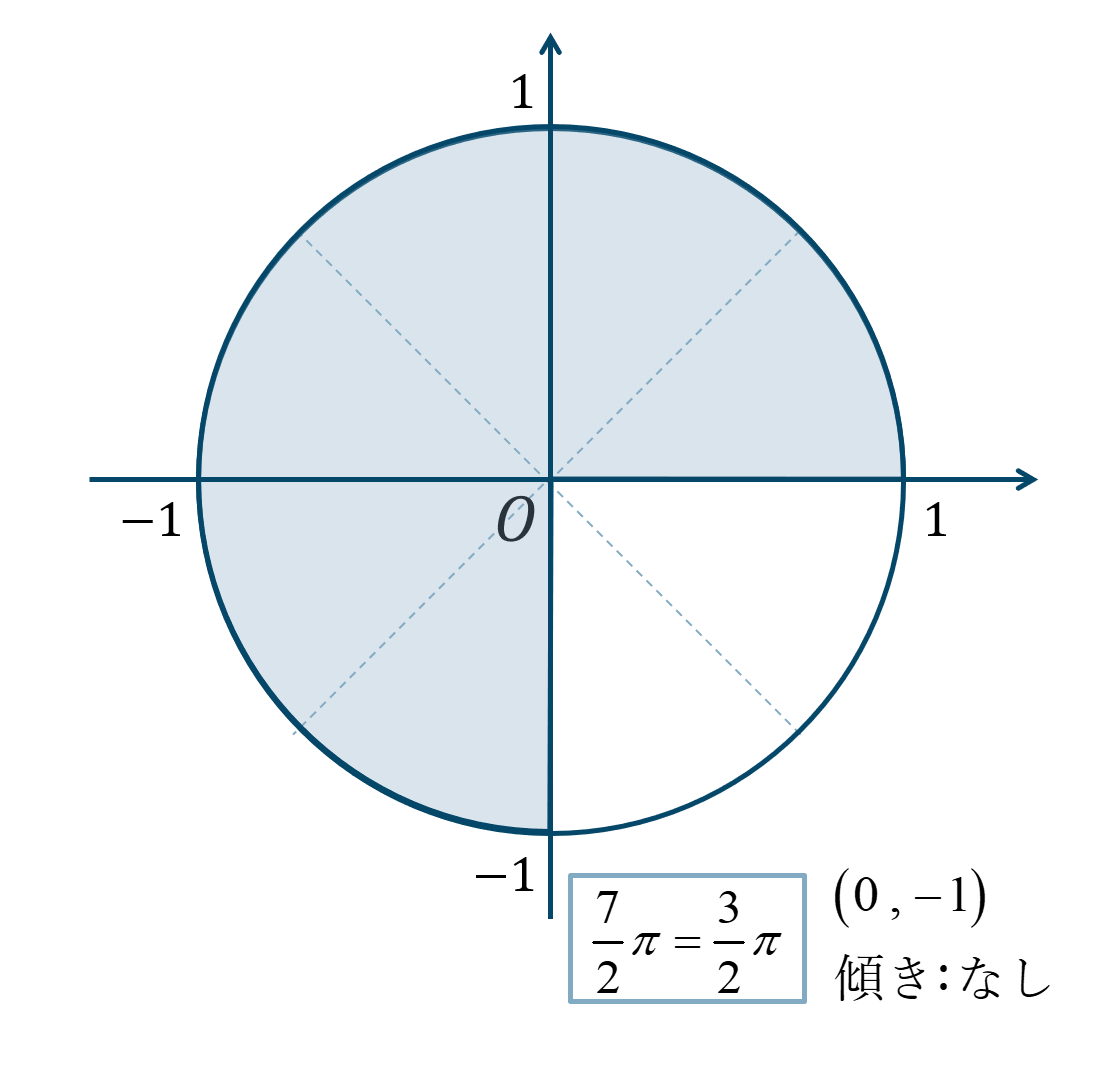
よって、答えは$$~~~\sin{\theta}=-1$$$$~~~\cos{\theta}=0$$また、\(\tan{\theta}\) は解なしとなります。



