三角関数の性質①

－θ、π－θ、π＋θの三角関数

Point：－θ、π－θ、π＋θの三角関数
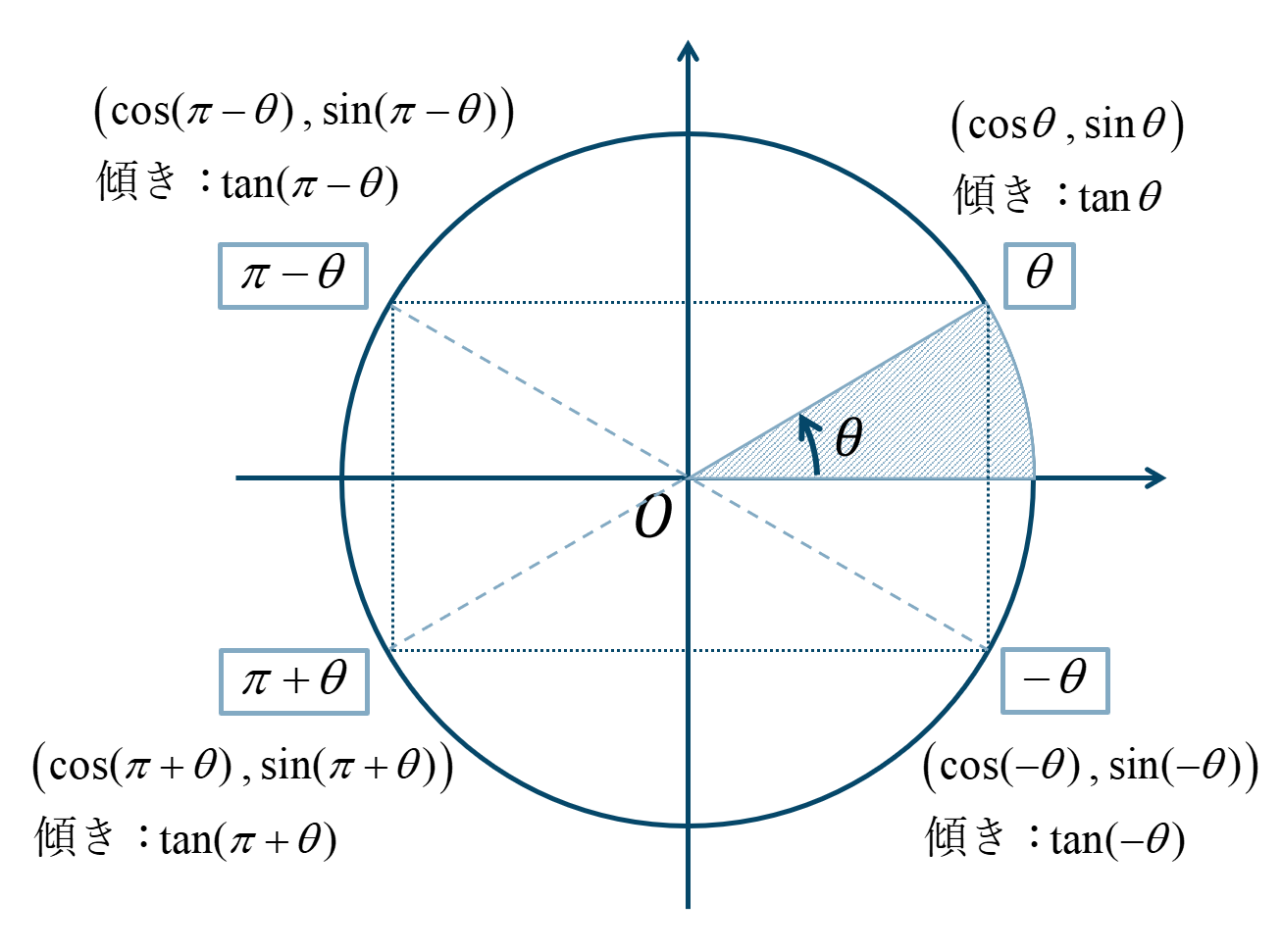
上の図の $\theta$ の三角関数を基準として考えます。
① $-\theta$ の三角関数
$y$ 座標は符号が逆なので、

$$\sin{(-\theta)}=-\sin{\theta}$$

$x$ 座標は同じ値なので、

$$\cos{(-\theta)}=\cos{\theta}$$

傾きは符号が逆なので、

$$\tan{(-\theta)}=-\tan{\theta}$$

 
② $\pi-\theta$ の三角関数
$y$ 座標は同じ値なので、

$$\sin{(\pi-\theta)}=\sin{\theta}$$

$x$ 座標は符号が逆なので、

$$\cos{(\pi-\theta)}=-\cos{\theta}$$

傾きは符号が逆なので、

$$\tan{(\pi-\theta)}=-\tan{\theta}$$

 
③ $\pi+\theta$ の三角関数
$y$ 座標は符号が逆なので、

$$\sin{(\pi+\theta)}=-\sin{\theta}$$

$x$ 座標は符号が逆なので、

$$\cos{(\pi+\theta)}=-\cos{\theta}$$

傾きは同じ値なので、

$$\tan{(\pi+\theta)}=\tan{\theta}$$

問題解説：三角関数の性質①

問題解説(1)

$$~~~~~~\sin{\theta}\cos{(-\theta)}+\sin{(\pi-\theta)}\cos{(\pi+\theta)}$$ 公式をそれぞれ用いて計算すると、 $$~=\sin{\theta}\cos{\theta}+\sin{\theta}(-\cos{\theta})$$ $$~=\sin{\theta}\cos{\theta}-\sin{\theta}\cos{\theta}$$ $$~=0$$ よって答えは $0$ となります。

問題解説(2)

$$~~~~~~\frac{\cos{(\pi-\theta)}\tan{(-\theta)}\tan{(\pi+\theta)}}{\sin{(\pi+\theta)}\tan{(\pi-\theta)}}$$ 公式をそれぞれ用いて計算すると、 $$~=\frac{-\cos{\theta}(-\tan{\theta})\tan{\theta}}{(-\sin{\theta})(-\tan{\theta})}$$ $$~=\frac{\cos{\theta}\tan{\theta}}{\sin{\theta}}$$ $\tan{\theta}={\Large \frac{\sin{\theta}}{\cos{\theta}}}$ を用いると、 $$~=\frac{\cos{\theta}\cdot{\Large \frac{\sin{\theta}}{\cos{\theta}}}}{\sin{\theta}}$$ $$~=\frac{\sin{\theta}}{\sin{\theta}}$$ $$~=1$$ よって、答えは $1$ となります。

今回のまとめ

これらの公式はそのまま暗記するのではなく、単位円を用いて導き出せるようになりましょう。

【問題一覧】数学Ⅱ：三角関数

このページは「高校数学Ⅱ：三角関数」の問題一覧ページとなります。解説の見たい単元名がわからないときは...

yorikuwa.com