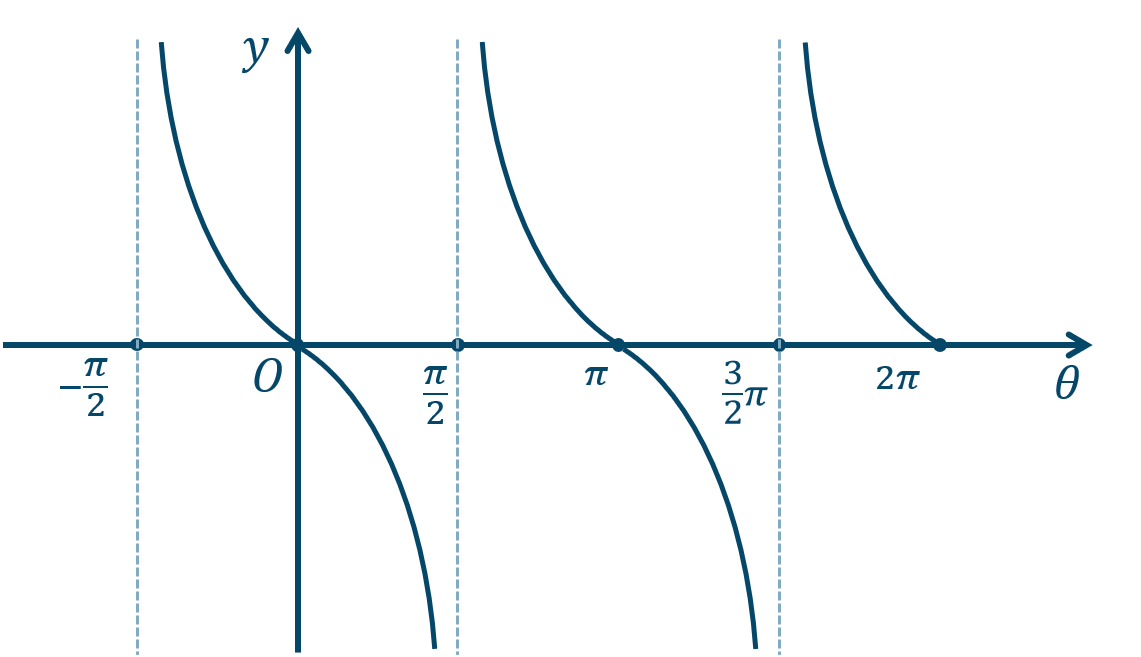
三角関数の縦幅の変化
また、\(y=-\sin{\theta}\) のグラフは、\(y=\sin{\theta}\) のグラフを \(\theta\) 軸で対称移動したグラフとなります。
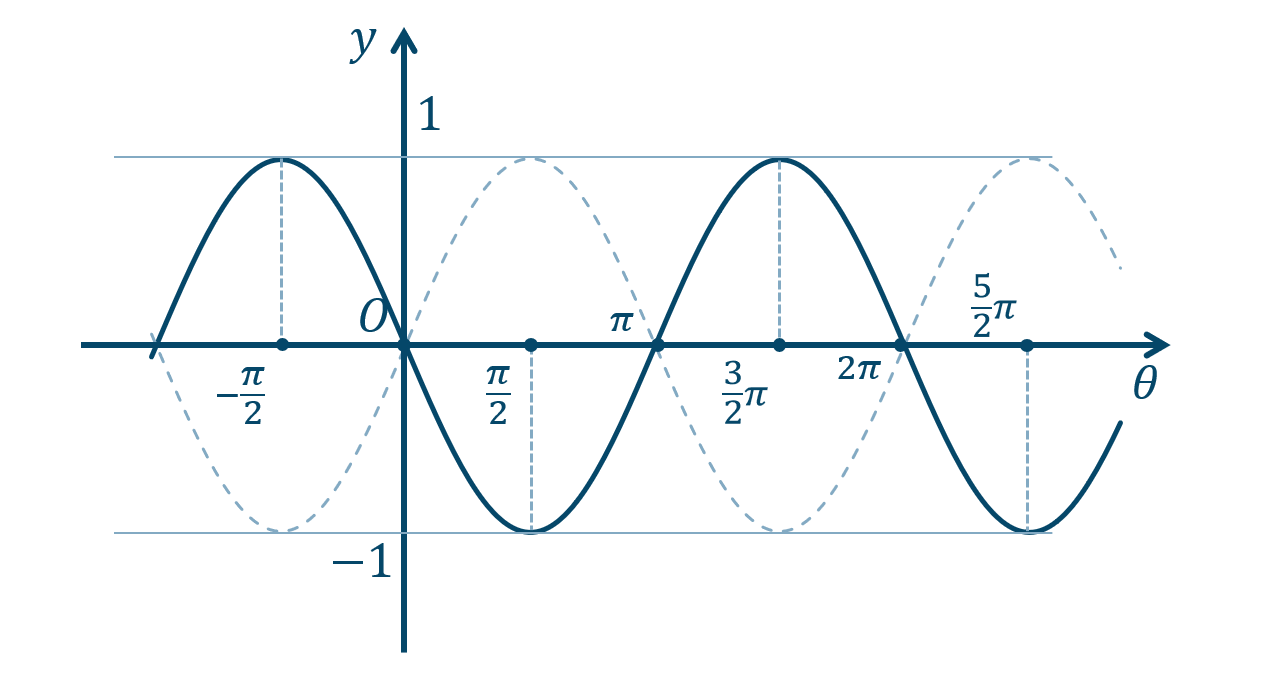
これらの周期は元の関数と同じになります。
問題:三角関数のグラフ②(縦幅の変化)
問題解説(1)
このグラフは \(y=\sin{\theta}\) のグラフを \(y\) 軸方向に \({\Large \frac{1}{2}}\) 倍したグラフとなります。
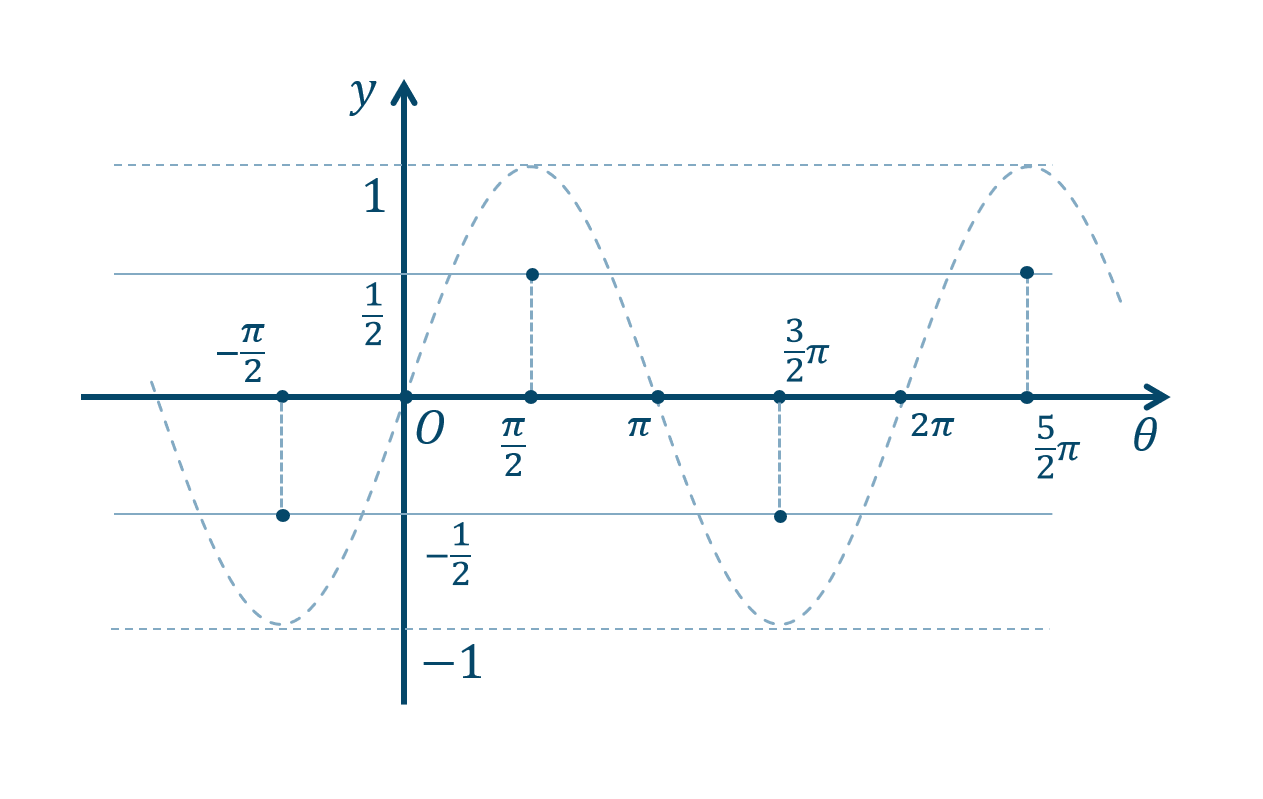
① 通る点などを書き込んでいきます。
\(\theta\) 軸上の点は、$$~~~~~0~,~\pi~,~2\pi~,~\cdots$$また、\(y=\pm{\Large \frac{1}{2}}\) となる点は、$$~~~-\frac{\pi}{2}~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$
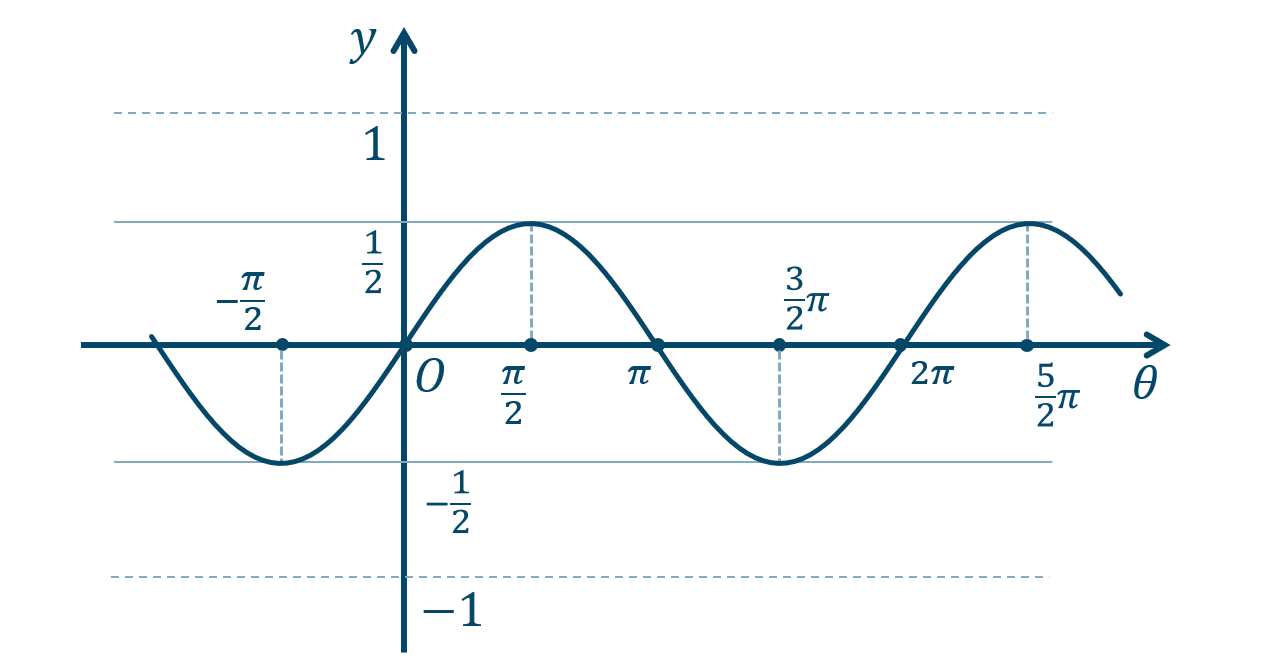
② 点を曲線で結びます。また、点の座標や、\(y=\pm{\Large \frac{1}{2}}\) の線を書き込みます。
また、この関数の周期は \(2\pi\) となります。
問題解説(2)
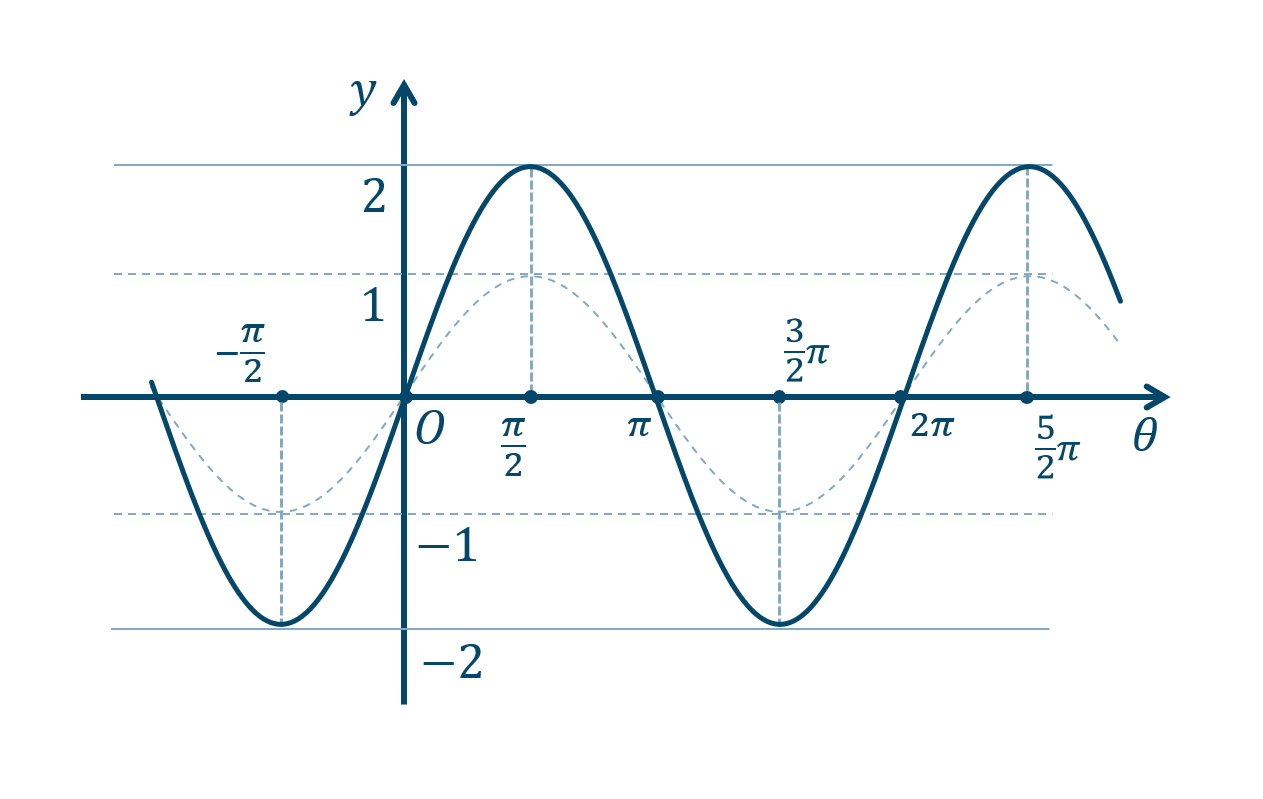
このグラフは \(y=\cos{\theta}\) のグラフを \(y\) 軸方向に \(2\) 倍したグラフとなります。
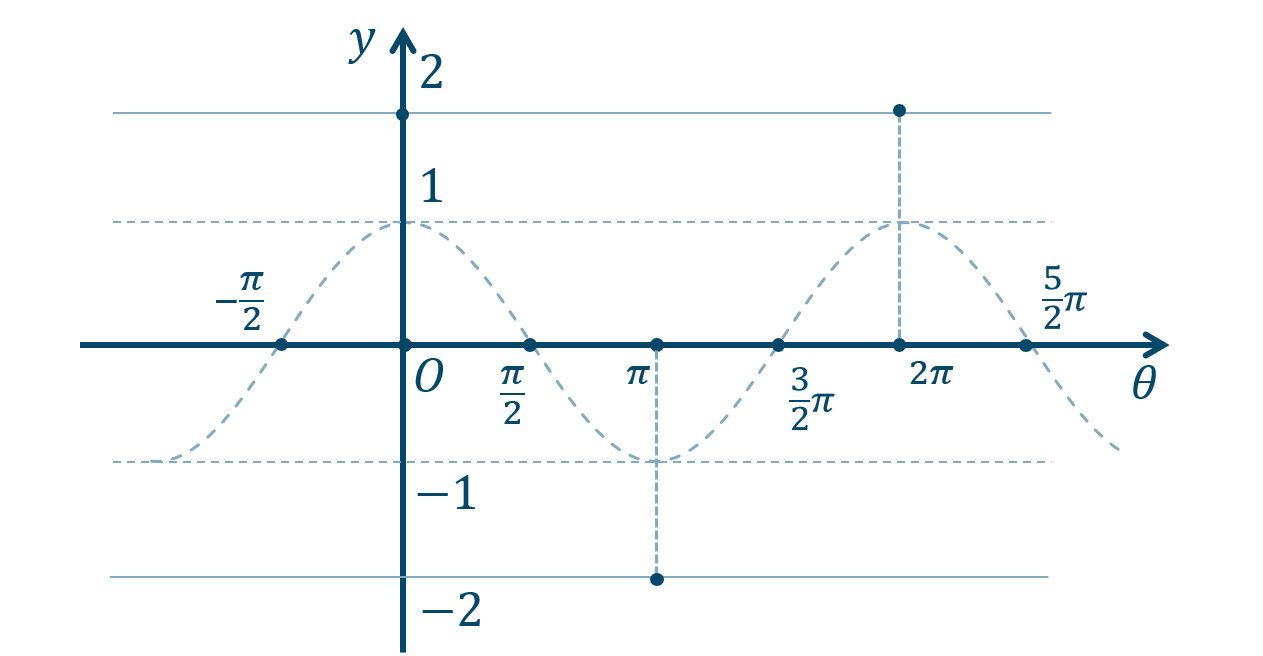
① 通る点などを書き込んでいきます。
\(\theta\) 軸上の点は、$$~~~-\frac{\pi}{2}~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$また、\(y=\pm2\) となる点は、$$~~~~~0~,~\pi~,~2\pi~,~\cdots$$
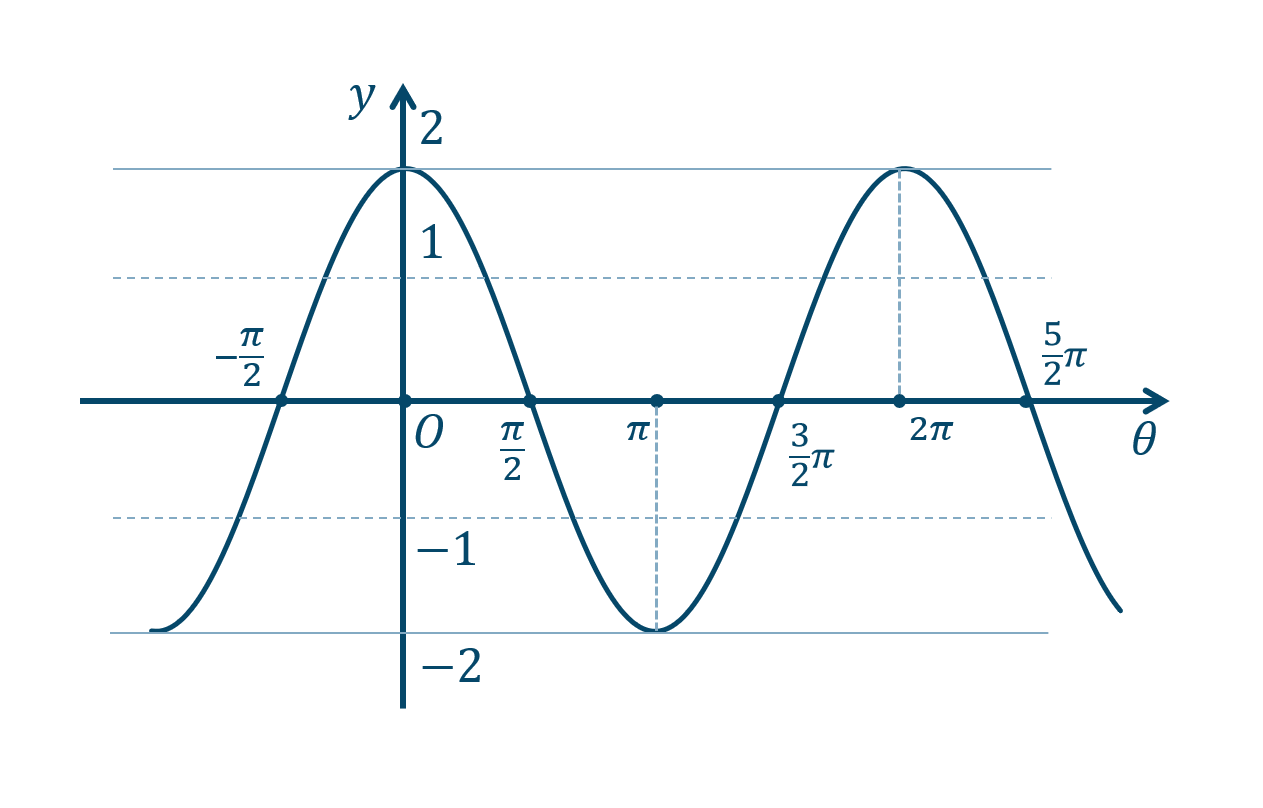
② 点を曲線で結びます。また、点の座標や、\(y=\pm2\) の線を書き込みます。
また、この関数の周期は \(2\pi\) となります。
問題解説(3)
このグラフは \(y=\tan{\theta}\) のグラフを \(\theta\) 軸で対称移動したグラフとなります。
① 通る点と漸近線を書き込んでいきます。
通る点は、$$~~~~~0~,~\pi~,~2\pi~,~\cdots$$また、漸近線の位置は、$$~~~-\frac{\pi}2~,~\frac{\pi}{2}~,~\frac{3}{2}\pi~,~\cdots$$
② 点を曲線で結んで、漸近線に近づくようにグラフを描きます。また、点の座標を書き込みます。
また、この関数の周期は \(\pi\) となります。
今回のまとめ
三角関数のグラフの描き方の基本は前回の方法と同じとなります。係数が付いているときは縦幅の変化に注意してグラフを描きましょう。