指数関数を含む２次方程式の解法
Point：指数関数を含む２次方程式解法の手順は、
① 与えられた式を \(a^x=t\) と置き換えるための式変形をします。
例えば、$$~~~9^x=(3^2)^x=(3^x)^2$$$$~~~2^{x+1}=2^x\cdot2^1=2\cdot2^x$$このような式変形をしましょう。
② \(a^x=t\) として、\(t\) の２次方程式とします。ただし、\(a^x>0\) より \(t>0\) となることに注意しましょう。
③ \(t\) の２次方程式を解きます。ここで解が \(t>0\) を満たすことに注意しましょう。
④ \(t=a^x\) と元に戻して、\(x\) の解を求めます。
① 与えられた式を \(a^x=t\) と置き換えるための式変形をします。
例えば、$$~~~9^x=(3^2)^x=(3^x)^2$$$$~~~2^{x+1}=2^x\cdot2^1=2\cdot2^x$$このような式変形をしましょう。
② \(a^x=t\) として、\(t\) の２次方程式とします。ただし、\(a^x>0\) より \(t>0\) となることに注意しましょう。
③ \(t\) の２次方程式を解きます。ここで解が \(t>0\) を満たすことに注意しましょう。
④ \(t=a^x\) と元に戻して、\(x\) の解を求めます。
問題解説：指数関数を含む２次方程式
問題次の方程式の解を求めよ。$$~~~3^{2x+1}+26\cdot3^x-9=0$$
$$~~~3^{2x+1}=3^{2x}\cdot3^1=(3^x)^2\cdot3=3(3^x)^2$$この式より与えられた式は、$$\hspace{ 15 pt}3^{2x+1}+26\cdot3^x-9=0$$$$\hspace{ 10 pt}3(3^x)^2+26\cdot3^x-9=0$$ここで、\(3^x=t\) とすると、\(t>0\) となります。よって、$$\hspace{ 10 pt}3t^2+26t-9=0$$たすき掛けの表より、
$$\hspace{ 10 pt}(3t-1)(t+9)=0$$よって、\(t\) の解は \(t>0\) より、$$~~~t=\frac{1}{3}$$（ \(t=-9\) は \(t<0\) より不適となります。）
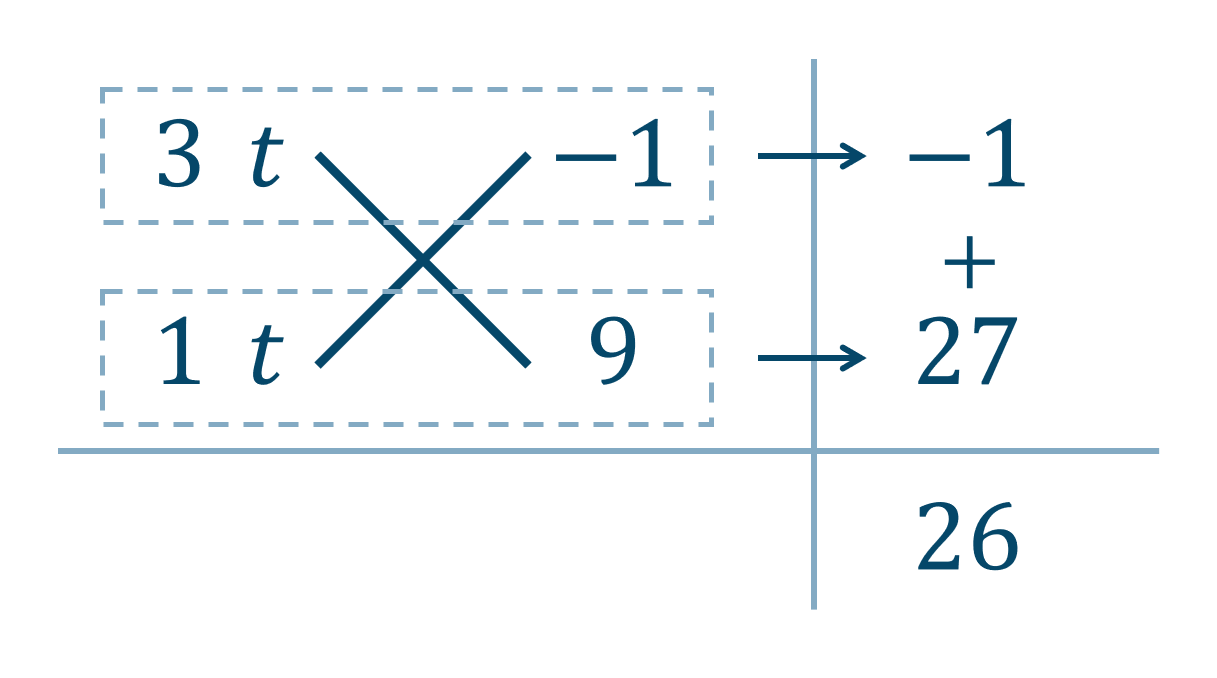
\(t=3^x\) と元に戻すと、$$\hspace{ 10 pt}3^x=\frac{1}{3}$$分数を累乗の形に式変形すると、$$\hspace{ 10 pt}3^x=3^{-1}$$指数部分を比較すると、$$\hspace{ 10 pt}x=-1$$
よって、答えは \(x=-1\) となります。
今回のまとめ
指数関数を含む２次方程式は、置き換えるための式変形の方法を覚えておきましょう。また、\(a^x=t\) としたときの \(t>0\) の範囲には注意しましょう。
【問題一覧】数学Ⅱ：指数関数と対数関数
このページは「高校数学Ⅱ：指数関数と対数関数」の問題一覧ページとなります。解説の見たい単元名がわから...
yorikuwa.com
