対数方程式の解法
① 真数条件より、\(x\) の値の範囲を求めます。
このとき、対数が複数あるときはそれぞれの真数条件より、共通範囲を求めます。
② 両辺をともに同じ底の対数で表し、和や差があるときは1つ対数で表します。
③ 両辺の真数部分のみを比較した式から \(x\) の値を求めます。
④ 求めた \(x\) が真数条件を満たしているか確認します。
問題解説:対数方程式
問題解説(1)
真数条件より、$$\hspace{ 10 pt}x-1>0$$移項すると、$$\hspace{ 10 pt}x>1$$
与式の右辺を、底を \(2\) とする対数で表すと、$$\hspace{ 10 pt}\log_{2}(x-1)=3$$$$\hspace{ 10 pt}\log_{2}(x-1)=3\cdot\log_{2}2$$係数を真数の累乗部分にすると、$$\hspace{ 10 pt}\log_{2}(x-1)=\log_{2}2^3$$$$\hspace{ 10 pt}\log_{2}(x-1)=\log_{2}8$$真数部分のみを比較すると、$$\hspace{ 10 pt}x-1=8$$移項すると、$$\hspace{ 10 pt}x=8+1$$$$\hspace{ 10 pt}x=9$$これは真数条件の \(x>1\) を満たします。
よって、答えは \(x=9\) となります。
問題解説(2)
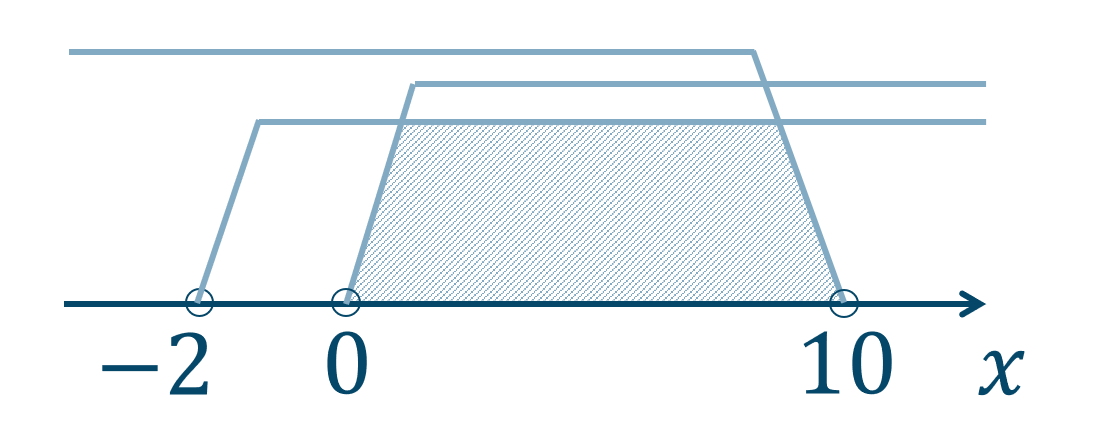
真数条件より、$$\hspace{ 10 pt}x>0~~~\cdots{\large ①}$$次に、$$\hspace{ 10 pt}x+2>0$$移項すると、$$\hspace{ 10 pt}x>-2~~~\cdots{\large ②}$$次に、$$\hspace{ 10 pt}10-x>0$$移項すると、$$\hspace{ 10 pt}-x>-10$$両辺に \(-1\) をかけると不等号の向きが逆になるので、$$\hspace{ 10 pt}x<10~~~\cdots{\large ③}$$よって、①〜③を数直線上に表すと、
よって、真数条件は$$~~~0<x<10$$となります。
与式は、$$\hspace{ 10 pt}\log_{2}x+\log_{2}(x+2)=\log_{2}(10-x)$$対数のたし算は真数のかけ算より、$$\hspace{ 10 pt}\log_{2}x(x+2)=\log_{2}(10-x)$$真数部分のみを比較すると、$$\hspace{ 10 pt}x(x+2)=10-x$$左辺を展開すると、$$\hspace{ 10 pt}x^2+2x=10-x$$移項すると、$$\hspace{ 10 pt}x^2+2x-10+x=0$$$$\hspace{ 10 pt}x^2+3x-10=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(x+5)(x-2)=0$$$$\hspace{ 50 pt}x=-5~,~2$$ここで、真数条件が \(0<x<10\) より \(x=-5\) は不適となります。
よって、答えは \(x=2\) となります。
今回のまとめ
対数方程式は、両辺を同じ底の対数で表して真数部分を比較して解きましょう。また、解が真数条件を満たしているかの確認を忘れないように!