3次不等式の証明の解法
Point:3次不等式の証明3次不等式の証明は、$$~~~ax^3+bx^2+cx+d≧0$$この不等式の左辺を \(y\) とした3次関数について、$$~~~y=ax^3+bx^2+cx+d$$この3次関数のグラフを増減表を用いて描いて、区間の中での最小値 \(m\) が \(m≧0\) となっていることを示します。
これより、区間の中で \(y≧0\) が示せて、3次不等式が証明できます。
これより、区間の中で \(y≧0\) が示せて、3次不等式が証明できます。
問題解説:3次不等式の証明
問題\(x≧0\) のとき、次の不等式を証明せよ。$$~~~x^3-3x^2+4≧0$$
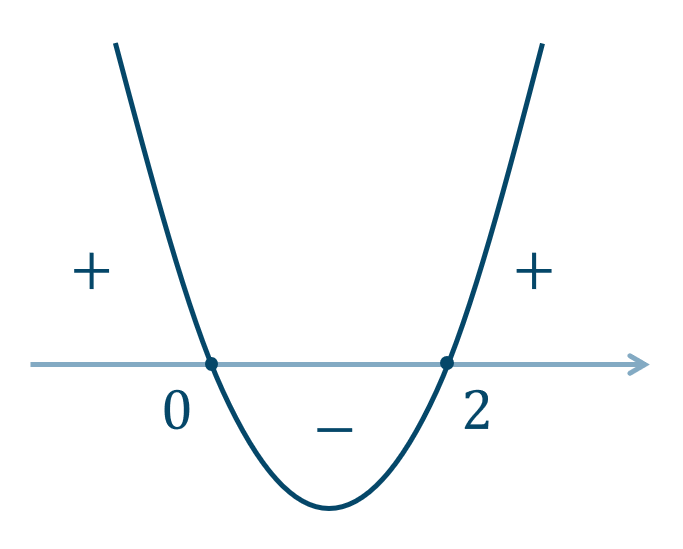
[証明] $$\hspace{ 10 pt}y=x^3-3x^2+4$$として、\(y\) を \(x\) で微分すると、$$\hspace{ 10 pt}y’=3x^2-6x$$右辺を因数分解すると、$$\hspace{ 21 pt}=3x(x-2)$$ここで、\(y’=0\) となるのは$$\hspace{ 20 pt}x=0~,~2$$これより、\(y’\) のグラフは次のようになります。
また、\(x=0\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=0^3-3\cdot0+4$$$$\hspace{ 18 pt}=4$$
\(x=2\) のとき \(y\) 座標は、$$\hspace{ 10 pt}y=2^3-3\cdot2^2+4$$$$\hspace{ 18 pt}=8-12+4$$$$\hspace{ 18 pt}=0$$
よって、\(y\) の増減表は次のようになります。
| \(x\) | \(\cdots\) | \(0\) | \(\cdots\) | \(2\) | \(\cdots\) |
| \(y’\) | \(+\) | \(0\) | \(-\) | \(0\) | \(+\) |
| \(y\) | ↗︎ | \(4\) | ↘︎ | \(0\) | ↗︎ |
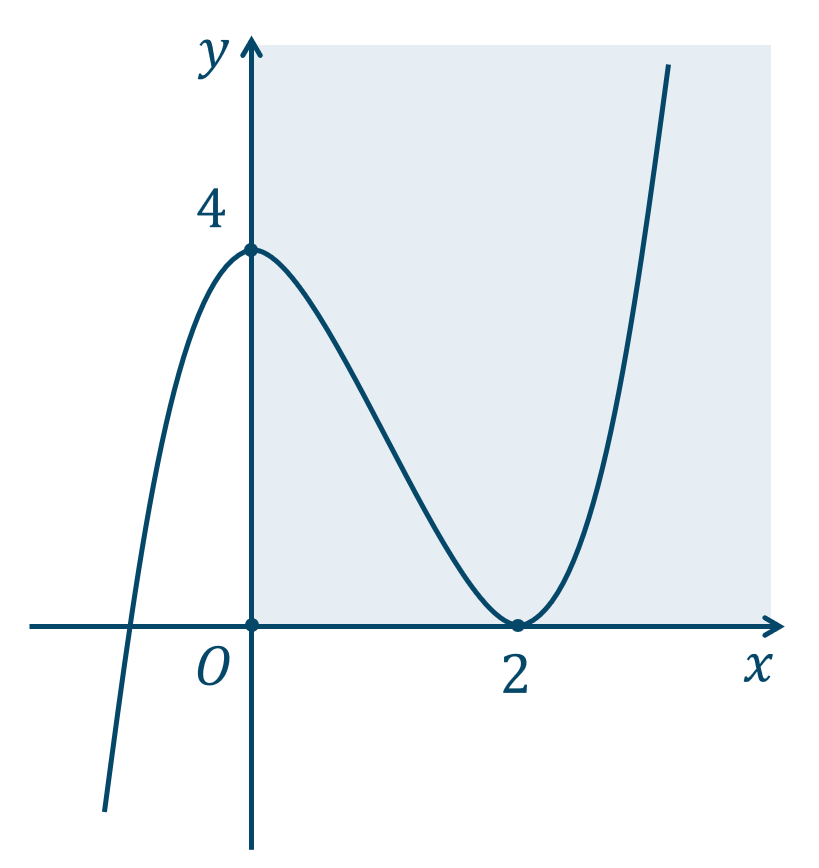
よって、\(x≧0\) でグラフは次のようになります。
グラフより \(y\) は \(x=2\) のとき最小値 \(0\) をとることより、\(x≧0\) で \(y≧0\) となります。
したがって、$$~~~x^3-3x^2+4≧0~~~(x≧0)$$[終]
今回のまとめ
3次不等式の証明は、与えられた3次式を3次関数としてグラフを描きます。グラフより最小値を求めて、その最小値を用いて不等式を証明する解法の手順を覚えておきましょう。

【問題一覧】数学Ⅱ:微分と積分
このページは「高校数学Ⅱ:微分と積分」の問題一覧ページとなります。解説の見たい単元名がわからないとき...