区間付きの面積
「 \(x\) 軸より上側か下側か」
または
「どちらのグラフが上か下か」
を考えて場合分けをして定積分を求めましょう。
問題解説:定積分と面積③(区間付きの面積)
問題解説(1)
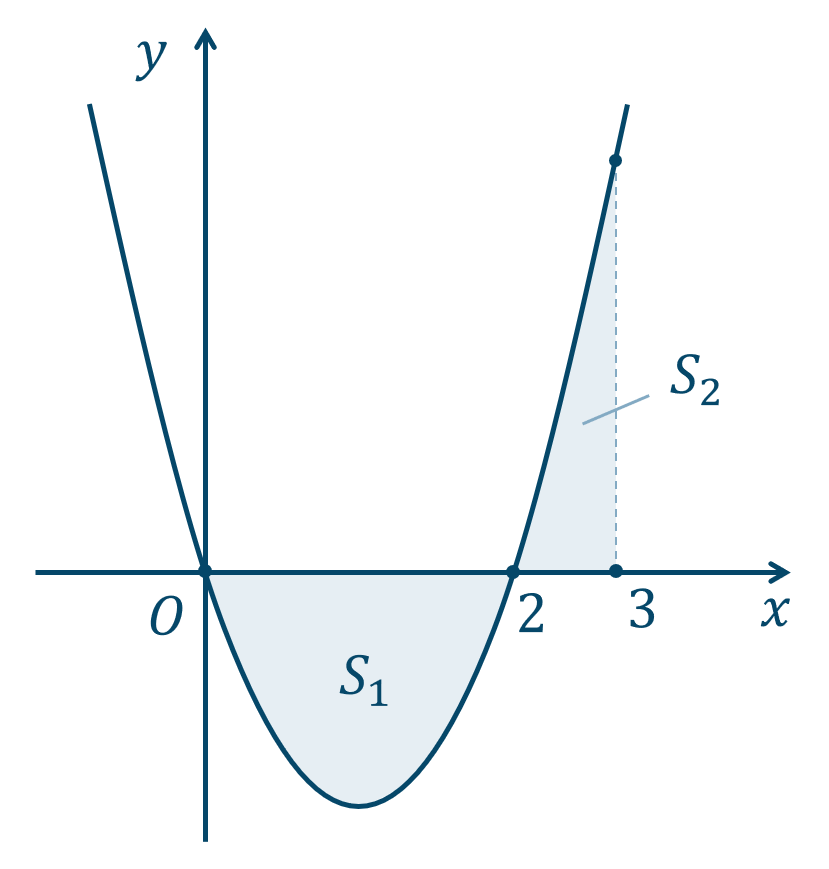
$$\hspace{ 10 pt}y=x^2-2x$$右辺を因数分解すると、$$\hspace{ 18 pt}=x(x-2)$$よって、この2次関数は \(x\) 軸と$$\hspace{ 20 pt}x=0~,~2$$で交わり、下に凸のグラフとなります。また、\(x=0\) \(,\) \(x=3\) \(,\) \(y=0\) で囲まれた図形は、次のようになります。
グラフより、
区間 \(0\) 〜 \(2\) では \(x\) 軸より下側にあり、区間 \(2\) 〜 \(3\) では \(x\) 軸より上側にあるので、求める図形の面積は、$$~~~-\int_{0}^{2}(x^2-2x)dx+\int_{2}^{3}(x^2-2x)dx$$
ここで、前半部分の定積分の計算は、$$~~~~~~-\int_{0}^{2}(x^2-2x)dx$$$$~=-\left[ \frac{1}{3}x^3-x^2 \right]_{0}^{2}~~~\cdots{\large ①}$$
ここで、①の [ ] の中の関数に \(x=2\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot2^3-2^2$$$$~=\frac{8}{3}-4$$$$~=\frac{8-12}{3}$$$$~=-\frac{4}{3}$$
また、\(x=0\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot0^3-0^2$$$$~=0$$
よって、①の計算の続きは、$$~~~~~~-\left[ \frac{1}{3}x^3-x^2 \right]_{0}^{2}$$$$~=-\left( -\frac{4}{3}-0 \right)$$$$~=\frac{4}{3}$$
次に後半部分の定積分の計算は、$$~~~~~~\int_{2}^{3}(x^2-2x)dx$$$$~=\left[ \frac{1}{3}x^3-x^2 \right]_{2}^{3}~~~\cdots{\large ②}$$
ここで、②の [ ] の中の関数に \(x=3\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot3^3-3^2$$$$~=9-9$$$$~=0$$
また、\(x=2\) を代入した値は、$$~~~~~~\frac{1}{3}\cdot2^3-2^2$$$$~=\frac{8}{3}-4$$$$~=\frac{8-12}{3}$$$$~=-\frac{4}{3}$$
よって、②の計算の続きは、$$~~~~~~\left[ \frac{1}{3}x^3-x^2 \right]_{2}^{3}$$$$~=0-\left( -\frac{4}{3} \right)$$$$~=\frac{4}{3}$$
以上より、求める面積は、$$~~~~~~-\int_{0}^{2}(x^2-2x)dx+\int_{2}^{3}(x^2-2x)dx$$$$~=\frac{4}{3}+\frac{4}{3}$$$$~=\frac{8}{3}$$
よって、答えは$$~~~\frac{8}{3}$$となります。
問題解説(2)
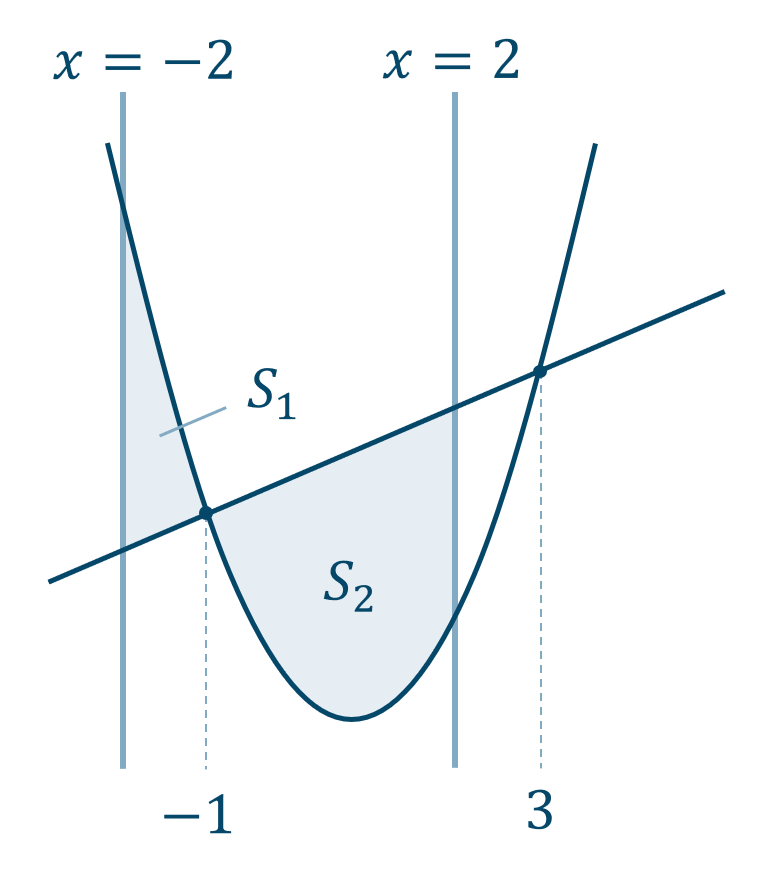
放物線と直線との交点の \(x\) 座標は、連立することにより、$$~~~\biggl\{ \begin{eqnarray} y=x^2 \\ y=2x+3 \end{eqnarray}$$連立すると、$$\hspace{ 10 pt}x^2=2x+3$$移項すると、$$\hspace{ 10 pt}x^2-2x-3=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(x+1)(x-3)=0$$$$\hspace{ 20 pt}x=-1~,~3$$したがって、交点の \(x\) 座標が \(x=-1~,~3\) となり、区間が \(-2≦x≦2\) で直線 \(x=-2\) と \(x=2\) を考えてグラフを描くと次のようになります。
よって、囲まれる図形は \(S_1\) と \(S_2\) に分けられる。
\(S_1\) の面積は区間が \(-2\) 〜 \(-1\) で \(y=x^2\) が上にきているので、$$~~~~~~\int_{-2}^{-1}\left\{ x^2-(2x+3) \right\}dx$$$$~=\int_{-2}^{-1}(x^2-2x-3)dx$$$$~=\left[ \frac{1}{3}x^3-x^2-3x \right]_{-2}^{-1}~~~\cdots{\large ①}$$
ここで、①の [ ] の中の関数に \(x=-1\) を代入した値は、$$~~~~~~\frac{1}{3}(-1)^3-(-1)^2-3(-1)$$$$~=-\frac{1}{3}-1+3$$$$~=-\frac{1}{3}+2$$$$~=\frac{-1+6}{3}$$$$~=\frac{5}{3}$$
また、\(x=-2\) を代入した値は、$$~~~~~~\frac{1}{3}(-2)^3-(-2)^2-3(-2)$$$$~=-\frac{8}{3}-4+6$$$$~=-\frac{8}{3}+2$$$$~=\frac{-8+6}{3}$$$$~=-\frac{2}{3}$$
よって、①の計算の続きは、$$~~~~~~\left[ \frac{1}{3}x^3-x^2-3x \right]_{-2}^{-1}$$$$~=\frac{5}{3}-\left( -\frac{2}{3} \right)$$$$~=\frac{5}{3}+\frac{2}{3}$$$$~=\frac{7}{3}$$
次に、\(S_2\) の面積は区間が \(-1\) 〜 \(2\) で \(y=2x+3\) が上にきているので、$$~~~~~~\int_{-1}^{2} \left\{ (2x+3)-x^2 \right\}dx$$$$~=\int_{-1}^{2}(-x^2+2x+3)dx$$$$~=\left[ -\frac{1}{3}x^3+x^2+3x \right]_{-1}^{2}~~~\cdots{\large ②}$$
ここで、②の [ ] の中の関数に \(x=2\) を代入した値は、$$~~~~~~-\frac{1}{3}\cdot2^3+2^2+3\cdot2$$$$~=-\frac{8}{3}+4+6$$$$~=-\frac{8}{3}+10$$$$~=\frac{-8+30}{3}$$$$~=\frac{22}{3}$$
\(x=-1\) を代入した値は、$$~~~~~~-\frac{1}{3}(-1)^3+(-1)^2+3(-1)$$$$~=\frac{1}{3}+1-3$$$$~=\frac{1}{3}-2$$$$~=\frac{1-6}{3}$$$$~=-\frac{5}{3}$$
よって、②の計算の続きは、$$~~~~~~\left[ -\frac{1}{3}x^3+x^2+3x \right]_{-1}^{2}$$$$~=\frac{22}{3}-\left( -\frac{5}{3} \right)$$$$~=\frac{22}{3}+\frac{5}{3}$$$$~=\frac{27}{3}$$$$~=9$$
したがって、求める面積 \(S_1+S_2\) は、$$~~~~~~\frac{7}{3}+9$$$$~=\frac{7+27}{3}$$$$~=\frac{34}{3}$$
よって、答えは$$~~~\frac{34}{3}$$となります。
今回のまとめ
区間付きの面積は、グラフを描いたときに区間によって状況が変化していれば、それぞれの場合で定積分の式を立てるようにしましょう。