２次曲線の弦の長さと中点

2020.10.01

２次曲線の弦の長さと中点の解法
問題解説：２次曲線の弦の長さと中点
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

２次曲線の弦の長さと中点の解法

Point：２次曲線の弦の長さと中点２次曲線 $f(x~,~y)=0$ と直線 $y=g(x)$ が交わってできる弦の長さと中点の座標は、
① $f(x~,~y)=0$ と $y=g(x)$ を連立して、$x$ の２次方程式とする。
② この２次方程式の２つの解を $\alpha~,~\beta$ とすると、解と係数の関係より、$$~~~\alpha+\beta~,~\alpha\beta$$
また、図示すると次のようになる。

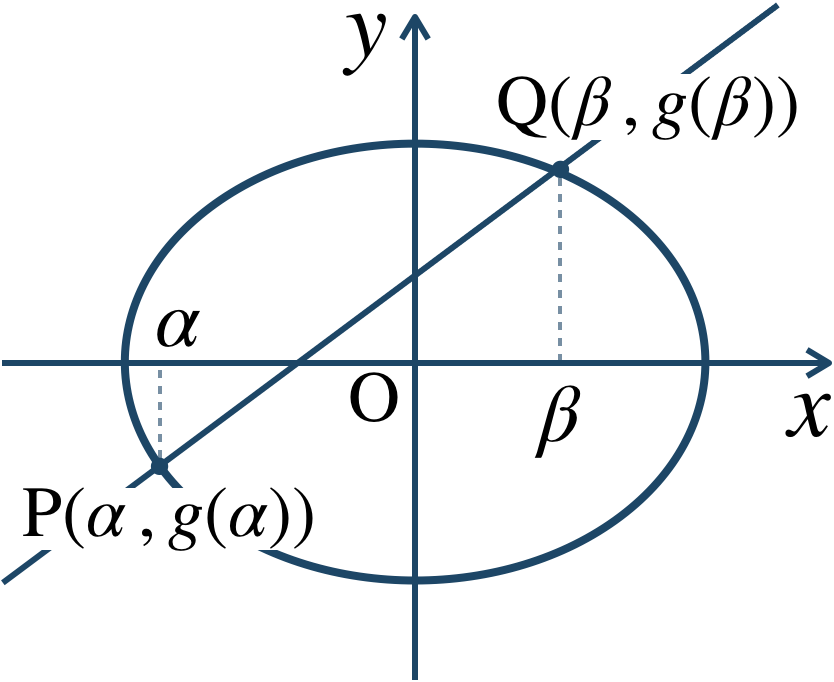
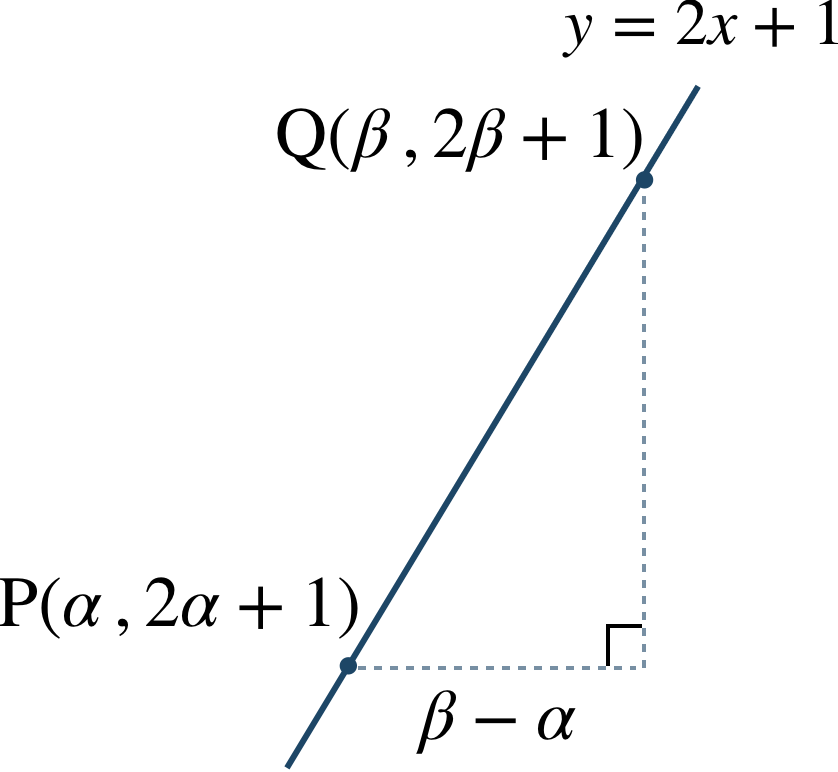
③ 弦の長さ ${\rm PQ}$ は、

$${\rm PQ}^2=(\beta-\alpha)^2+\{g(\beta)-g(\alpha)\}^2$$

解と係数の関係の $\alpha+\beta~,~\alpha\beta$ を代入して値を求める。
④ 中点 ${\rm M}$ の座標は、

$${\rm M}\left(\frac{\,\alpha+\beta \,}{\,2 \,}~,~\frac{\,g(\alpha)+g(\beta) \,}{\,2 \,}\right)$$

解と係数の関係の $\alpha+\beta$ を代入して座標を求める。

問題解説：２次曲線の弦の長さと中点

問題解説(1)

問題楕円 $5x^2+y^2=5$ と直線 $y=2x+1$ が交わってできる弦について、次の問いに答えよ。
${\small (1)}~$弦の長さを求めよ。

$5x^2+y^2=5$ に $y=2x+1$ を代入すると、$$~~~5x^2+(2x+1)^2=5$$展開して移項すると、$$~~~5x^2+4x^2+4x+1-5=0$$$$\hspace{46pt} 9x^2+4x-4=0$$この２つの解を $\alpha~,~\beta$ とすると、解と係数の関係より、$$~~~\left\{~ \begin{eqnarray} \alpha+\beta=-\frac{\,4 \,}{\,9 \,} \\\alpha\beta=-\frac{\,4 \,}{\,9 \,} \end{eqnarray}\right.$$
また、２つの共有点の座標は $x$ 座標が $x=\alpha~,~\beta$ であるので、$y=2x+1$ より、$$~~~{\rm P}(\alpha~,~2\alpha+1)~,~{\rm Q}(\beta~,~2\beta+1)$$

よって、${\rm }$ の長さは、$$~~~~~~{\rm PQ}^2$$$$~=(\beta-\alpha)^2+\{(2\beta+1)-(2\alpha+1)\}^2$$$$~=(\beta-\alpha)^2+(2\beta-2\alpha)^2$$$$~=(\beta-\alpha)^2+2^2(\beta-\alpha)^2$$$$~=(\beta-\alpha)^2+4(\beta-\alpha)^2$$$$~=5(\beta-\alpha)^2$$ここで、
等式 $(\beta-\alpha)^2=(\alpha+\beta)^2-4\alpha\beta$
より、$$~=5\{\alpha+\beta)^2-4\alpha\beta\}$$$\alpha+\beta~,~\alpha\beta$ の値を代入すると、$$~=5\left\{\left(-\frac{\,4 \,}{\,9 \,}\right)^2-4\left(-\frac{\,4 \,}{\,9 \,}\right)\right\}$$$$~=5\left(\frac{\,16 \,}{\,81 \,}+\frac{\,16 \,}{\,9 \,}\right)$$$$~=5\times\frac{\,16+144 \,}{\,81 \,}$$$$~=\frac{\,5\times160 \,}{\,81 \,}$$$$~=\frac{\,800 \,}{\, 81\,}$$よって、${\rm PQ}^2={\large \frac{\,800\,}{\,81\,}}$ となるので、$$~~~{\rm PQ}=\sqrt{\frac{\,800 \,}{\,81 \,}}=\frac{\,20\sqrt{2} \,}{\,9 \,}$$したがって、弦の長さは ${\large \frac{\,20\sqrt{2}\,}{\,9\,}}$ となる。

問題解説(2)

問題楕円 $5x^2+y^2=5$ と直線 $y=2x+1$ が交わってできる弦について、次の問いに答えよ。
${\small (2)}~$弦の中点の座標を求めよ。

弦 ${\rm PQ}$ の中点 ${\rm M}$ を図示すると、

よって、$x$ 座標は、$$~~~x=\frac{\,\alpha+\beta \,}{\,2 \,}$$(1) の $\alpha+\beta=-{\large \frac{\,4\,}{\,9\,}}$ を代入すると、$$~~~x=-\frac{\, 4\,}{\,9 \,}\times\frac{\,1 \,}{\, 2\,}=-\frac{\,2 \,}{\,9 \,}$$また、$y=2x+1$ 上の点より、$$~~~y=2\times\left(-\frac{\,2 \,}{\,9 \,}\right)+1$$$$~~~~~=-\frac{\,4 \,}{\,9 \,}+1$$$$~~~~~=\frac{\,-4+9 \,}{\,9 \,}$$$$~~~~~=\frac{\,5 \,}{\,9 \,}$$したがって、中点の座標は、$$~~~\left(-\frac{\,2 \,}{\,9 \,}~,~\frac{\,5 \,}{\,9 \,}\right)$$となる。