２次曲線と離心率

2020.10.03

２次曲線と離心率の解法
問題解説：２次曲線と離心率
今回のまとめ

２次曲線と離心率の解法

Point：２次曲線と離心率定点 ${\rm F}$ からの距離 ${\rm PF}$ と定直線 $l$ からの距離 ${\rm PH}$ の比の値 $e$ が一定である点 ${\rm P}$ の軌跡は、点 ${\rm F}$ を焦点の１つとする２次曲線となる。

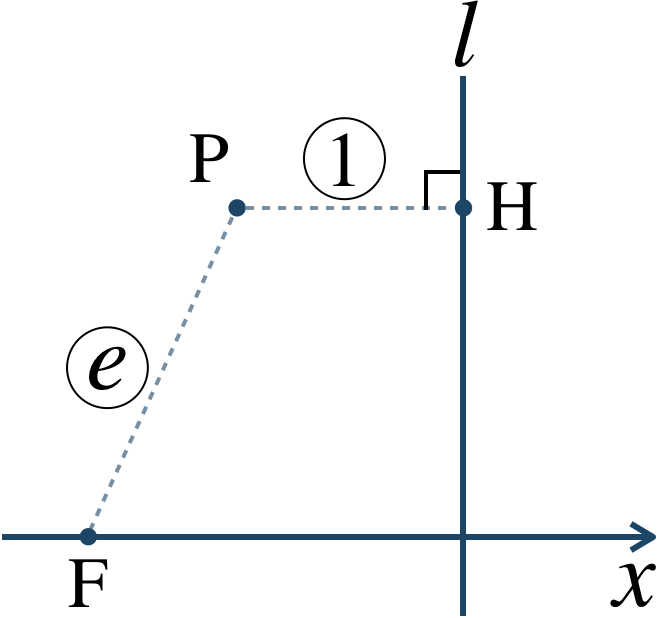
よって、$$~~~{\rm PF}\,:\,{\rm PH}=e\,:\,1$$となり、$l$ を準線、$e$ を離心率という。
また、$e$ の値より、
　$0\lt e\lt 1$ のとき、楕円
　$e=1$ のとき、放物線
　$e\gt 1$ のとき、双曲線
となる。

問題解説：２次曲線と離心率

問題解説(1)

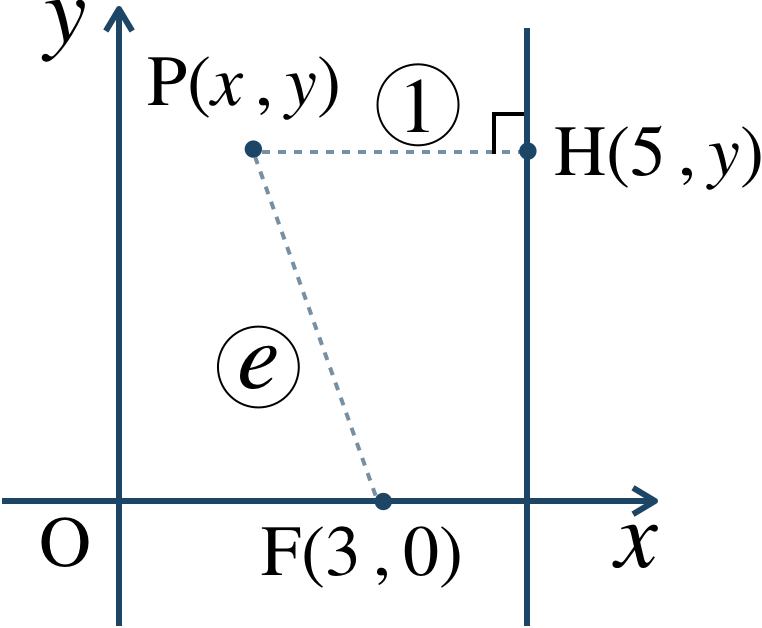
問題点 $(3~,~0)$ と直線 $x=5$ からの距離の比が $e\,:\,1$ である点 ${\rm P}$ について、$e$ の値が次のときの点 ${\rm P}$ の軌跡を求めよ。$${\small (1)}~e=1$$

点 ${\rm P}$ の座標を $(x~,~y)$ とする。
点 ${\rm P}$ から直線 $x=5$ に下した垂線を ${\rm PH}$ とすると、点 ${\rm H}(5~,~y)$ となる。

よって、${\rm PF}$ と ${\rm PH}$ はそれぞれ$$~~~{\rm PF}^2=(x-3)^2+(y-0)^2$$$$~~~~~~~~~\,=(x-3)^2+y^2~~~\cdots~{\large ①}$$$$~~~{\rm PH}^2=(x-5)^2+(y-y)^2$$$$~~~~~~~~~~=(x-5)^2~~~\cdots~{\large ②}$$となる。
また、${\rm PF}\,:\,{\rm PH}=e\,:\,1$ より、$$~~~{\rm PF}=e{\rm PH}$$両辺を２乗すると、$$~~~{\rm PF}^2=e^2{\rm PH}^2~~~\cdots~{\large ③}$$
③に $e=1$ と①、②を代入すると、$$~~~(x-3)^2+y^2=1^2\cdot(x-5)^2$$展開すると、$$~~~x^2-6x+9+y^2=x^2-10x+25$$移項すると、$$~~~y^2=x^2-10x+25-x^2+6x-9$$$$~~~y^2=-4x+16$$$$~~~y^2=-4(x-4)$$したがって、放物線 $y^2=-4x$ を $x$ 軸方向に$4$ 平行移動した放物線となる。

問題解説(2)

問題点 $(3~,~0)$ と直線 $x=5$ からの距離の比が $e\,:\,1$ である点 ${\rm P}$ について、$e$ の値が次のときの点 ${\rm P}$ の軌跡を求めよ。$${\small (2)}~e=\sqrt{3}$$

(1) の③に $e=\sqrt{3}$ と①、②を代入すると、$$~~~(x-3)^2+y^2=\left(\sqrt{3}\right)^2\cdot(x-5)^2$$展開すると、$$~~~x^2-6x+9+y^2=3(x^2-10x+25)$$$$~~~x^2-6x+9+y^2=3x^2-30x+75$$移項すると、$$~~~x^2-6x+9+y^2-3x^2+30x-75=0$$$$\hspace{55pt} -2x^2+24x-66+y^2=0$$両辺を $\times(-1)$ すると、$$~~~2x^2-24x+66-y^2=0$$$x$ について平方完成すると、$$~~~~~~~~~~~\,2(x^2-12x)+66-y^2=0$$$$~~~2\{(x-6)^2-36\}+66-y^2=0$$$$~~~~~~\,2(x-6)^2-72+66-y^2=0$$$$~~~~~~~~~~~~~~~~~2(x-6)^2-6-y^2=0$$移項すると、$$~~~2(x-6)^2-y^2=6$$両辺を $\div6$ すると、$$~~~\frac{\,2(x-6)^2 \,}{\,6 \,}-\frac{\,y^2 \,}{\, 6\,}=\frac{\, 6\,}{\,6 \,}$$$$~~~~~\frac{\,(x-6)^2 \,}{\,3 \,}-\frac{\,y^2 \,}{\, 6\,}=1$$したがって、双曲線 ${\large \frac{\,x^2\,}{\,3\,}}-{\large \frac{\,y^2\,}{\,6\,}}=1$ を $x$ 軸方向に$6$ 平行移動した双曲線となる。

問題解説(3)

問題点 $(3~,~0)$ と直線 $x=5$ からの距離の比が $e\,:\,1$ である点 ${\rm P}$ について、$e$ の値が次のときの点 ${\rm P}$ の軌跡を求めよ。$${\small (3)}~e=\frac{\,1 \,}{\,\sqrt{3} \,}$$

(1) の③に $e={\large \frac{\,1\,}{\,\sqrt{3}\,}}$ と①、②を代入すると、$$~~~(x-3)^2+y^2=\left(\frac{\,1 \,}{\, \sqrt{3}\,}\right)^2\cdot(x-5)^2$$展開すると、$$~~~x^2-6x+9+y^2=\frac{\,1 \,}{\,3 \,}(x^2-10x+25)$$両辺を $\times3$ すると、$$~~~3x^2-18x+27+3y^2=x^2-10x+25$$移項して、計算すると、$$~~~3x^2-18x+27+3y^2-x^2+10x-25=0$$$$\hspace{74pt} ~~2x^2-8x+2+3y^2=0$$$x$ について平方完成すると、$$~~~~~~~~~~~\,2(x^2-4x)+2+3y^2=0$$$$~~~2\{(x-2)^2-4\}+2+3y^2=0$$$$~~~~~~\,2(x-2)^2-8+2+3y^2=0$$$$~~~~~~~~~~~~~2(x-2)^2-6+3y^2=0$$移項すると、$$~~~2(x-2)^2+3y^2=6$$両辺を $\div6$ すると、$$~~~\frac{\,2(x-2)^2 \,}{\,6 \,}+\frac{\,3y^2 \,}{\, 6\,}=\frac{\, 6\,}{\,6 \,}$$$$~~~~~~~\frac{\,(x-2)^2 \,}{\,3 \,}+\frac{\,y^2 \,}{\, 2\,}=1$$したがって、楕円 ${\large \frac{\,x^2\,}{\,3\,}}+{\large \frac{\,y^2\,}{\,2\,}}=1$ を $x$ 軸方向に$2$ 平行移動した楕円となる。