複素数の極形式

2020.09.09

複素数の極形式の解法
問題解説：複素数の極形式
今回のまとめ

複素数の極形式の解法

Point：複素数の極形式$0$ でない複素数 $z=a+bi$ について、複素数平面上に ${\rm P}(z)$ を表すと、

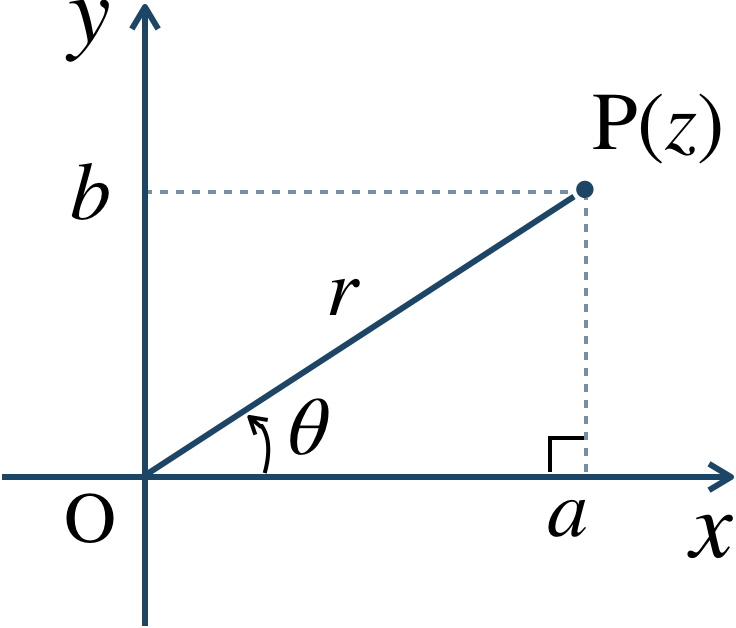
このとき、

$${\rm OP}=r=|z|=\sqrt{a^2+b^2}$$

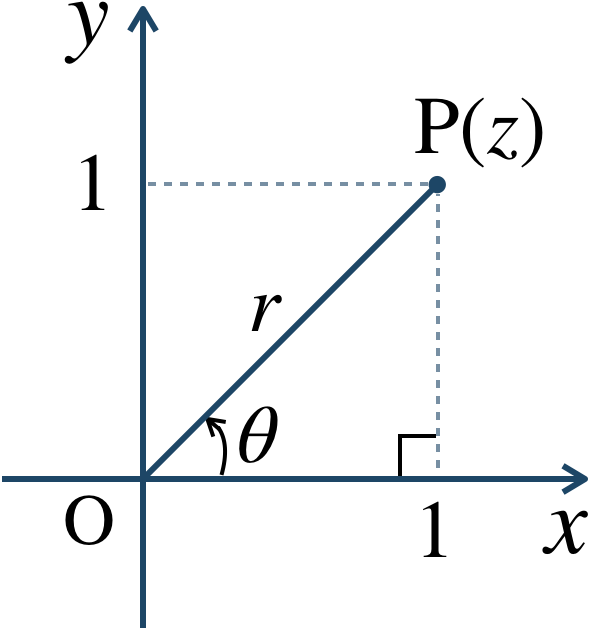
次に、実軸の正の部分と ${\rm OP}$ とのなす角を $\theta$ とする。この $\theta$ を偏角といい、

$$\arg z=\theta$$

と表す。
したがって、$z=a+bi$ の極形式を

$$z=r\left(\cos{\theta}+i\sin{\theta}\right)$$

で表す。

解法の手順は、
① $z=a+bi$ より、絶対値 $r$ を求める。$$~~~r=|z|=\sqrt{a^2+b^2}$$② $z$ を複素数平面上に表し、偏角 $\theta$ を求める。
③ 極形式を求める。$$~~~z=r\left(\cos{\theta}+i\sin{\theta}\right)$$

問題解説：複素数の極形式

問題解説(1)

問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (1)}~1+i$$

$z=1+i$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{1^2+1^2}$$$$~~~~=\sqrt{1+1}=\sqrt{2}$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は、$$~~~\theta=\frac{\,\pi\,}{\,4\,}$$したがって、極形式は、$$~~~\sqrt{2}\left(\cos{\frac{\,\pi\,}{\,4\,}}+i\sin{\frac{\,\pi\,}{\,4\,}}\right)$$となる。

問題解説(2)

問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (2)}~-1+i$$

$z=-1+i$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{(-1)^2+1^2}$$$$~~~~=\sqrt{1+1}=\sqrt{2}$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は、$$~~~\theta=\frac{\,3\,}{\,4\,}\pi$$したがって、極形式は、$$~~~\sqrt{2}\left(\cos{\frac{\,3\,}{\,4\,}\pi}+i\sin{\frac{\,3\,}{\,4\,}\pi}\right)$$となる。

問題解説(3)

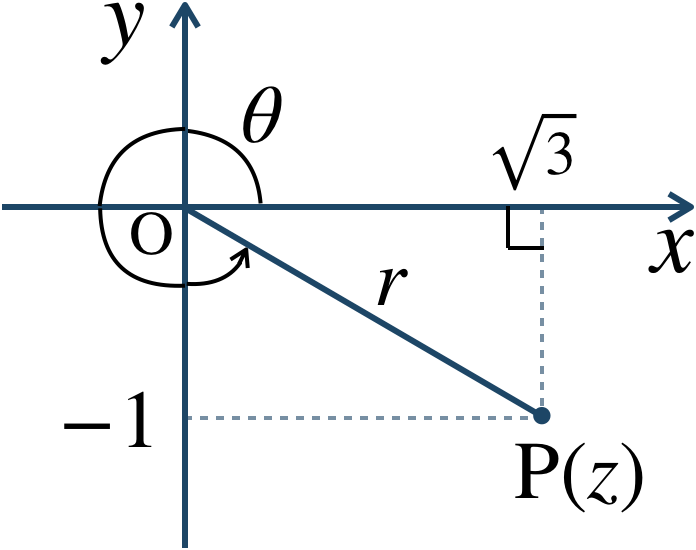
問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (3)}~\sqrt{3}-i$$

$z=\sqrt{3}-i$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{(\sqrt{3})^2+(-1)^2}$$$$~~~~=\sqrt{3+1}=\sqrt{4}=2$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は $0≦\theta\lt 2\pi$ の範囲で、$$~~~\theta=\frac{\,11\,}{\,6\,}\pi$$したがって、極形式は、$$~~~2\left(\cos{\frac{\,11\,}{\,6\,}\pi}+i\sin{\frac{\,11\,}{\,6\,}\pi}\right)$$となる。

問題解説(4)

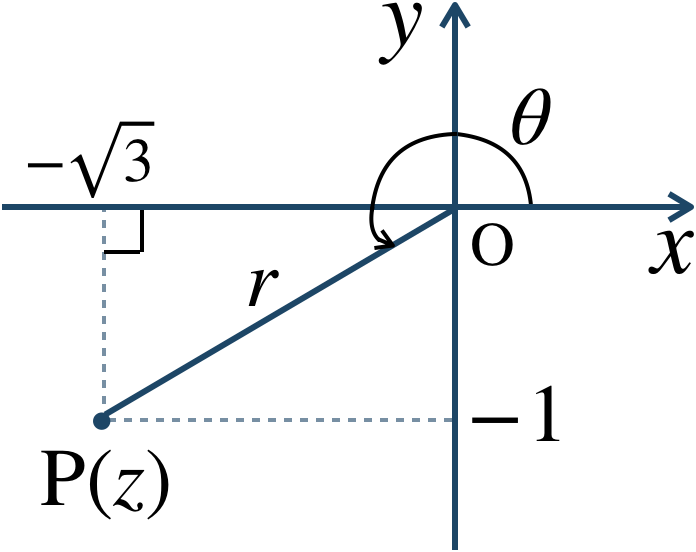
問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (4)}~-3-\sqrt{3}i$$

$z=-3-\sqrt{3}i$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{(-3)^2+(-\sqrt{3})^2}$$$$~~~~=\sqrt{9+3}=\sqrt{12}=2\sqrt{3}$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は $0≦\theta\lt 2\pi$ の範囲で、$$~~~\theta=\frac{\,7\,}{\,6\,}\pi$$したがって、極形式は、$$~~~2\sqrt{3}\left(\cos{\frac{\,7\,}{\,6\,}\pi}+i\sin{\frac{\,7\,}{\,6\,}\pi}\right)$$となる。

問題解説(5)

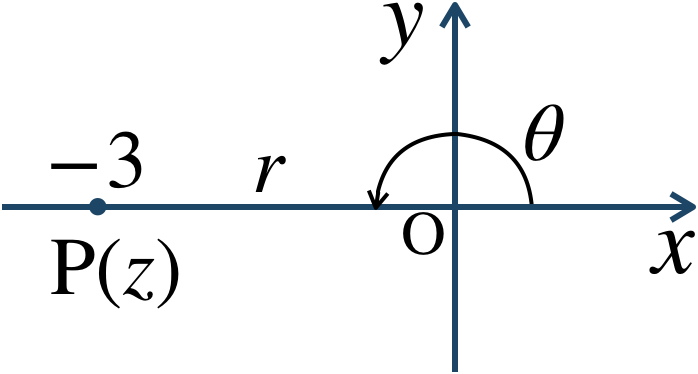
問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (5)}~-3$$

$z=-3$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{(-3)^2+0^2}$$$$~~~~=\sqrt{9+0}=\sqrt{9}=3$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は $0≦\theta\lt 2\pi$ の範囲で、$$~~~\theta=\pi$$したがって、極形式は、$$~~~3\left(\cos{\pi}+i\sin{\pi}\right)$$となる。

問題解説(6)

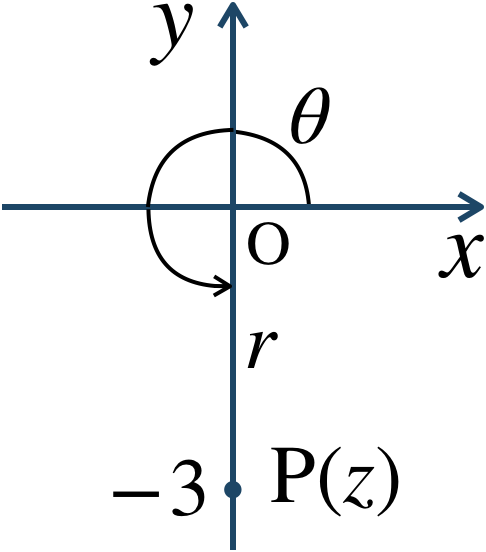
問題次の複素数を極形式で表せ。ただし、偏角 $\theta$ は $0≦\theta\lt 2\pi$ とする。$${\small (6)}~-3i$$

$z=-3i$ とすると、$$~~~r=|z|$$$$~~~~=\sqrt{0^2+(-3)^2}$$$$~~~~=\sqrt{0+9}=\sqrt{9}=3$$また、$z$ を複素数平面上に表すと、

図より、偏角 $\theta$ は $0≦\theta\lt 2\pi$ の範囲で、$$~~~\theta=\frac{\,3\,}{\,2\,}\pi$$したがって、極形式は、$$~~~3\left(\cos{\frac{\,3\,}{\,2\,}\pi}+i\sin{\frac{\,3\,}{\,2\,}\pi}\right)$$となる。