極形式の積と商の解法
■ 積 \(z_1z_2\)
絶対値はそれぞれの積より、$$~~~|z_1z_2|=|z_1||z_2|=r_1r_2$$偏角はそれぞれの和より、$$~~~~~\arg(z_1z_2)$$$$~=\arg z_1+\arg z_2=\theta_1+\theta_2$$したがって、積の極形式は、
■ 商 \({\Large \frac{\,z_1\,}{\,z_2\,}}\)
絶対値はそれぞれの商より、$$~~~\left| \frac{\,z_1\,}{\,z_2\,}\right|=\frac{\,|z_1| \,}{\,|z_2| \,}=\frac{\,r_1 \,}{\,r_2 \,}$$偏角はそれぞれの差より、$$~~~~~\arg \left(\frac{\,z_1 \,}{\,z_2 \,}\right)$$$$~=\arg z_1-\arg z_2=\theta_1-\theta_2$$したがって、商の極形式は、
問題解説:極形式の積と商
問題解説(1)
\(\alpha=-1+\sqrt{3}i\) について、
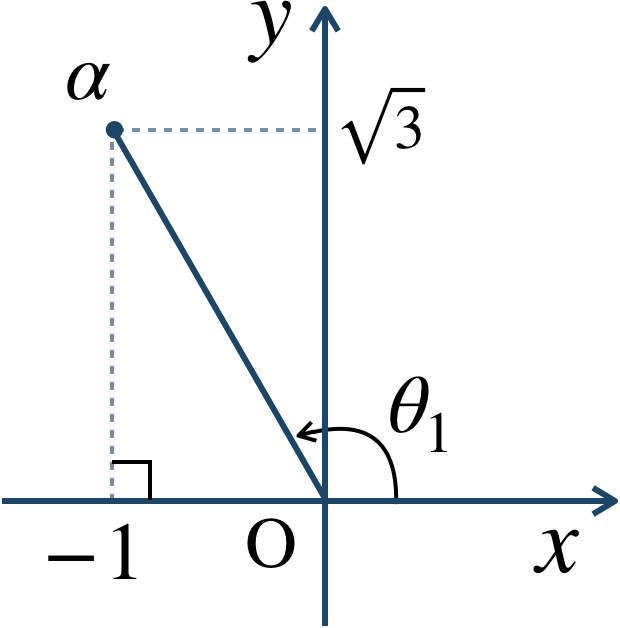
絶対値は、$$~~~~~~|\alpha|$$$$~=\sqrt{(-1)^2+(\sqrt{3})^2}$$$$~=\sqrt{1+3}=\sqrt{4}=2$$また、\(\alpha\) を複素数平面上に表すと、
図より、偏角 \(\theta_1\) は、$$~~~\theta_1=\frac{\,2 \,}{\,3 \,}\pi$$よって、\(\alpha\) の極形式は、$$~~~\alpha=2\left(\cos{\frac{\,2 \,}{\,3 \,}\pi}+i\sin{\frac{\,2 \,}{\,3 \,}\pi}\right)~~~\cdots~{\large ①}$$
\(\beta=2-2i\) について、
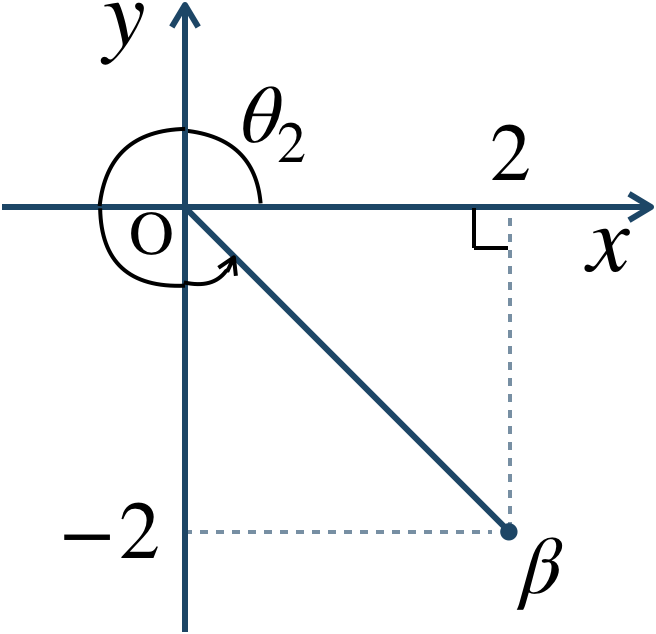
絶対値は、$$~~~~~~|\beta|$$$$~=\sqrt{2^2+(-2)^2}$$$$~=\sqrt{4+4}=\sqrt{8}=2\sqrt{2}$$また、\(\beta\) を複素数平面上に表すと、
図より、偏角 \(\theta_2\) は、$$~~~\theta_2=\frac{\,7 \,}{\,4 \,}\pi$$よって、\(\beta\) の極形式は、$$~~~\beta=2\sqrt{2}\left(\cos{\frac{\,7 \,}{\,4 \,}\pi}+i\sin{\frac{\,7 \,}{\,4 \,}\pi}\right)~~~\cdots~{\large ②}$$
積 \(\alpha\beta\) について、
絶対値は、$$~~~~~~|\alpha\beta|$$$$~=|\alpha||\beta|$$$$~=2\times2\sqrt{2}=4\sqrt{2}$$また、偏角は、$$~~~~~~\arg (\alpha\beta)$$$$~=\arg \alpha +\arg \beta$$$$~=\frac{\,2 \,}{\,3 \,}\pi+\frac{\,7 \,}{\,4 \,}\pi$$$$~=\frac{\,8+21 \,}{\,12 \,}\pi$$$$~=\frac{\,29 \,}{\,12 \,}\pi$$ここで、偏角 \(\theta\) は \(0≦\theta\lt2\pi\) であるので、$$~~~\frac{\,29 \,}{\,12 \,}\pi=2\pi+\frac{\,5 \,}{\,12 \,}\pi$$これより、偏角は、$$~~~\arg (\alpha\beta)=\frac{\,5 \,}{\,12 \,}\pi$$したがって、極形式は、$$~~~\alpha\beta=4\sqrt{2}\left(\cos{\frac{\,5 \,}{\,12 \,}\pi}+i\sin{\frac{\,5 \,}{\,12 \,}\pi}\right)$$となる。
【別解】
\(\beta\) の極形式を求めるとき、偏角を \(-{\large \frac{\,\pi\,}{\,4\,}}\) と考えてもよい。よって、極形式は、$$~~~\beta=2\sqrt{2}\left\{ \cos{\left(-\frac{\,\pi \,}{\,4 \,}\right)}+i\sin{\left(-\frac{\,\pi \,}{\,4 \,}\right)}\right\}$$
問題解説(2)
(1) の①と②より、\({\large \frac{\,\alpha\,}{\,\beta\,}}\) について、
絶対値は、$$~~~~~~\left|\frac{\,\alpha \,}{\,\beta \,}\right|$$$$~=\frac{\,|\alpha| \,}{\,|\beta| \,}$$$$~=\frac{\,2 \,}{\,2\sqrt{2} \,}=\frac{\, 1\,}{\,\sqrt{2} \,}=\frac{\,\sqrt{2} \,}{\,2 \,}$$また、偏角は、$$~~~~~~\arg \left(\frac{\,\alpha \,}{\,\beta \,}\right)$$$$~=\arg \alpha -\arg \beta$$$$~=\frac{\,2 \,}{\,3 \,}\pi-\frac{\,7 \,}{\,4 \,}\pi$$$$~=\frac{\,8-21 \,}{\,12 \,}\pi$$$$~=-\frac{\,13 \,}{\,12 \,}\pi$$ここで、偏角 \(\theta\) は \(0≦\theta\lt2\pi\) であるので、$$~~~-\frac{\,13 \,}{\,12 \,}\pi=\frac{\,11 \,}{\,12 \,}\pi-\frac{\, 24\,}{\, 12\,}\pi$$$$~~~~~~~~~~~~~~~~~=\frac{\,11 \,}{\,12 \,}\pi+2\pi\times(-1)$$これより、偏角は、$$~~~\arg \left(\frac{\,\alpha \,}{\,\beta \,}\right)=\frac{\,11\,}{\,12 \,}\pi$$したがって、極形式は、$$~~~\frac{\,\alpha \,}{\,\beta \,}=\frac{\,\sqrt{2} \,}{\,2 \,}\left(\cos{\frac{\,11 \,}{\,12 \,}\pi}+i\sin{\frac{\,11 \,}{\,12 \,}\pi}\right)$$となる。
今回のまとめ
複素数の極形式の積と商の計算方法を見てきました。それぞれの絶対値と偏角の計算を覚えていきましょう。