複素数の回転移動の解法
となる。
また、\(\theta\) 回転するだけの場合は \(r=1\) となり、
となる。
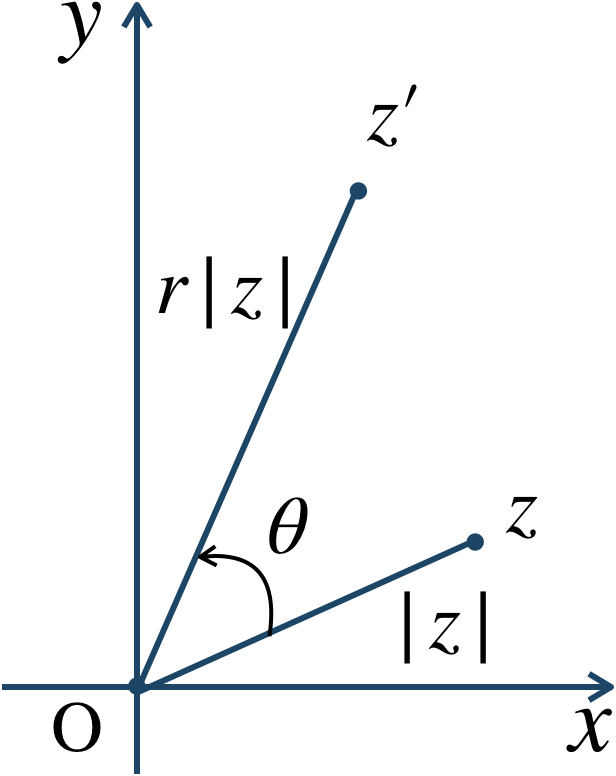
このことより、逆に、$$~~~r(\cos{\theta}+i\sin{\theta})\cdot z$$この式は、点 \(z\) を原点を中心に \(\theta\) だけ回転し、原点からの距離を \(r\) 倍した点となる。
問題解説:複素数の回転移動
問題解説(1)
\({\small (1)}~\)\(z=1+\sqrt{3}i\) とするとき、点 \(z\) を原点を中心に次の角だけ回転した点の複素数を求めよ。$$~{\large ①}~\frac{\, \pi\,}{\,3 \,}~~~~~~~~~~{\large ②}~-\frac{\,\pi \,}{\,6 \,}$$
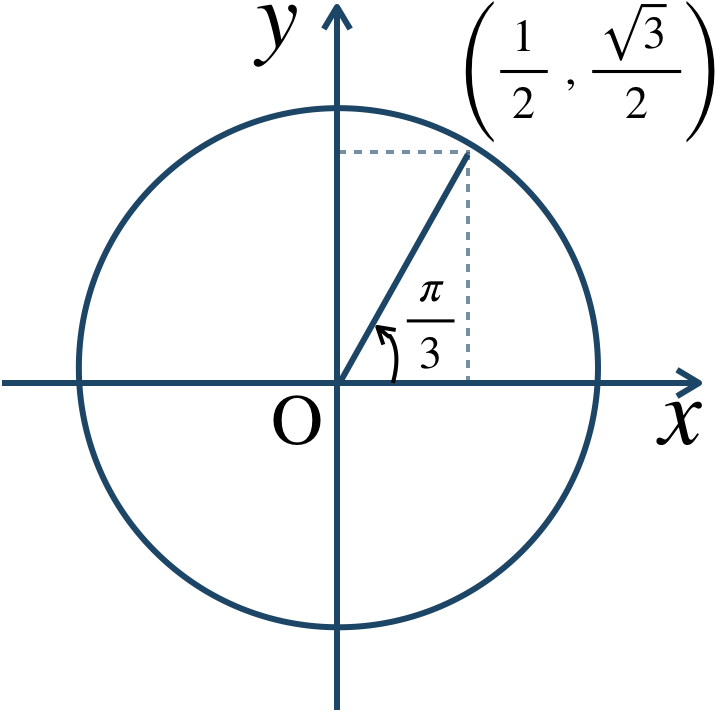
\({\large ①}~z\) を \({\large \frac{\,\pi\,}{\,3\,}}\) だけ回転するので、$$~~~~~~\left(\cos{\frac{\,\pi \,}{\,3 \,}}+i\sin{\frac{\,\pi \,}{\,3 \,}}\right)\cdot z$$\(\sin{}~,~\cos{}\) を計算すると、単位円より、
$$~=\left(\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i\right)\cdot z$$\(z=1+\sqrt{3}i\) を代入すると、$$~=\left(\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i\right)(1+\sqrt{3}i)$$$$~=\frac{\,1 \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}i+\frac{\,\sqrt{3} \,}{\,2 \,}i+\frac{\,3 \,}{\,2 \,}i^2$$\(i^2=-1\) より、$$~=\frac{\,1 \,}{\,2 \,}-\frac{\,3 \,}{\, 2\,}+\left(\frac{\,\sqrt{3} \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\,2 \,}\right)i$$$$~=-1+\sqrt{3}i$$したがって、回転した点の複素数は、$$~~~-1+\sqrt{3}i$$
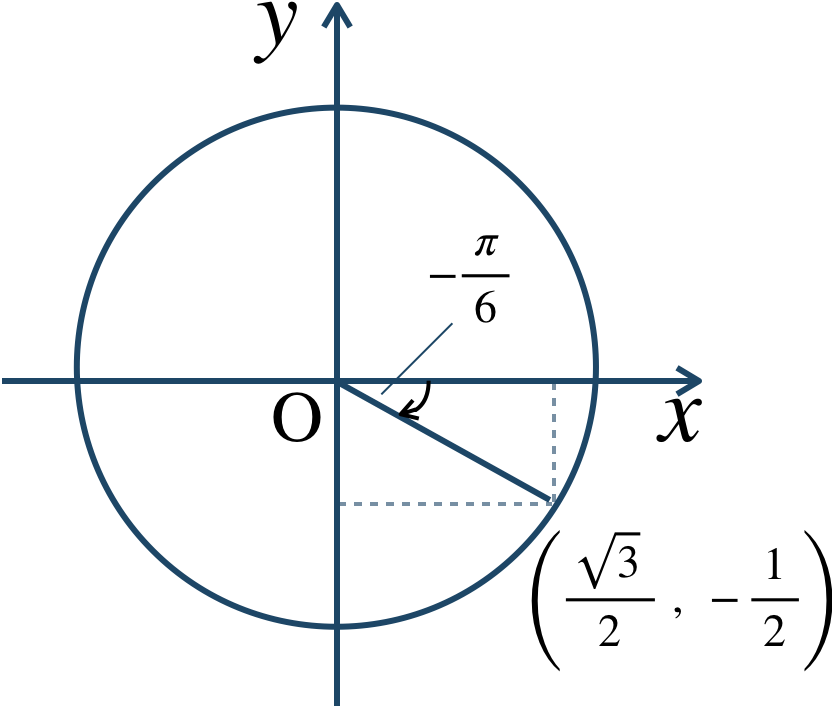
\({\large ②}~z\) を \(-{\large \frac{\,\pi\,}{\,6\,}}\) だけ回転するので、$$~~~~~~\left\{ \cos\left(-{\frac{\,\pi \,}{\,6 \,}}\right)+i\sin\left(-{\frac{\,\pi \,}{\,6 \,}}\right)\right\} \cdot z$$\(\sin{}~,~\cos{}\) を計算すると、単位円より、
$$~=\left(\frac{\,\sqrt{3} \,}{\,2 \,}-\frac{\,1 \,}{\,2 \,}i\right)\cdot z$$\(z=1+\sqrt{3}i\) を代入すると、$$~=\left(\frac{\,\sqrt{3} \,}{\,2 \,}-\frac{\,1 \,}{\,2 \,}i\right)(1+\sqrt{3}i)$$$$~=\frac{\,\sqrt{3} \,}{\,2 \,}+\frac{\,3 \,}{\,2 \,}i-\frac{\,1 \,}{\,2 \,}i+\frac{\,\sqrt{3} \,}{\,2 \,}i^2$$\(i^2=-1\) より、$$~=\frac{\,\sqrt{3} \,}{\,2 \,}+\frac{\,\sqrt{3} \,}{\, 2\,}+\left(\frac{\,3 \,}{\,2 \,}-\frac{\,1 \,}{\,2 \,}\right)i$$$$~=\sqrt{3}+i$$したがって、回転した点の複素数は、$$~~~\sqrt{3}+i$$
問題解説(2)
\({\small (2)}~\)次の複素数は点 \(z\) をどのように移動した点か答えよ。$$~{\large ①}~(1+i)z~~~~~~~~~~{\large ②}~(\sqrt{3}-i)z$$
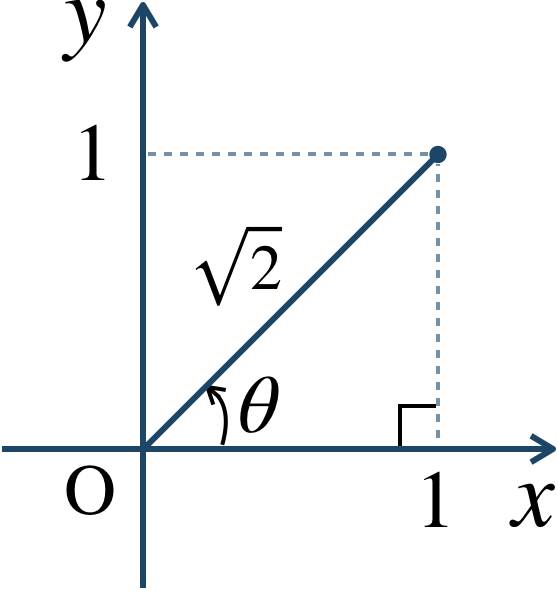
\({\large ①}~\) 複素数 \(1+i\) について、絶対値は、$$~~~~~~|1+i|$$$$~=\sqrt{1^2+1^2}=\sqrt{1+1}=\sqrt{2}$$また、複素数平面上に表すと、
図より、偏角は \({\large \frac{\,\pi\,}{\,4\,}}\) となるので、極形式は、$$~~~\sqrt{2}\left(\cos{\frac{\,\pi \,}{\,4 \,}}+i\sin{\frac{\,\pi \,}{\,4 \,}}\right)$$したがって、\((1+i)z\) は点 \(z\) を原点を中心に \({\large \frac{\,\pi\,}{\,4\,}}\) だけ回転して、原点からの距離を \(\sqrt{2}\) 倍した点となる。
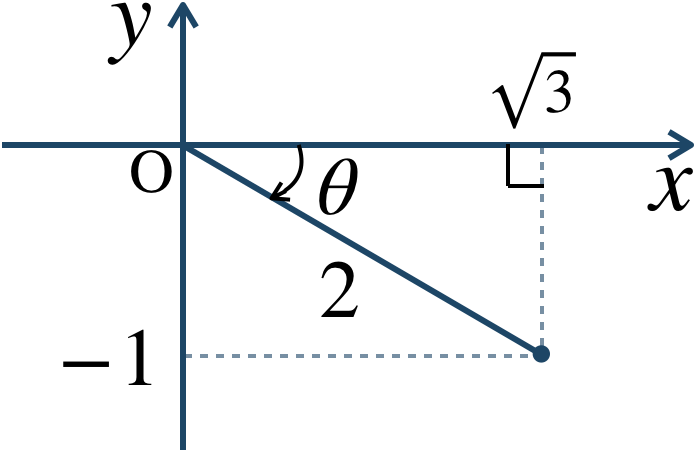
\({\large ②}~\) 複素数 \(\sqrt{3}-i\) について、絶対値は、$$~~~~~~|\sqrt{3}-i|$$$$~=\sqrt{(\sqrt{3})^2+(-1)^2}$$$$~=\sqrt{3+1}=\sqrt{4}=2$$また、複素数平面上に表すと、
図より、偏角は \(-{\large \frac{\,\pi\,}{\,6\,}}\) となる(ここでの偏角は範囲指定がないので、実軸から近い方で考える。)ので、極形式は、$$~~~2\left\{ \cos\left(-{\frac{\,\pi \,}{\,6 \,}}\right)+i\sin\left(-{\frac{\,\pi \,}{\,6 \,}}\right)\right\} $$したがって、\((\sqrt{3}-i)z\) は点 \(z\) を原点を中心に \(-{\large \frac{\,\pi\,}{\,6\,}}\) だけ回転して、原点からの距離を \(2\) 倍した点となる。
今回のまとめ
複素数平面上での点の回転移動について解説していきました。かけ算する複素数の式でどのように回転移動するかをおさえておきましょう。