複素数平面上の三角形の形状の解法
① 条件式を、$$~~~\frac{\,\beta-\alpha \,}{\, \gamma-\alpha\,}=a+bi$$と式変形する。
② \(a+bi\) を極形式にする。
絶対値 \(r\) 、偏角 \(\theta\) より、$$~~~a+bi=r(\cos{\theta}+i\sin{\theta})$$③ 辺の条件は、$$~~~\left|\frac{\,\beta-\alpha \,}{\,\gamma-\alpha \,}\right|={\rm \frac{\,AB \,}{\,AC \,}}=r$$となり、比で表すと、$$~~~{\rm AB\,:\,AC}=r\,:\,1$$④ 角の条件は、$$~~~\arg \left(\frac{\,\beta-\alpha \,}{\,\gamma-\alpha \,}\right)=\angle{\rm CAB}=\theta$$⑤ 辺の条件と角の条件より、三角形の形状を決める。
問題解説:複素数平面上の三角形の形状
問題解説(1)
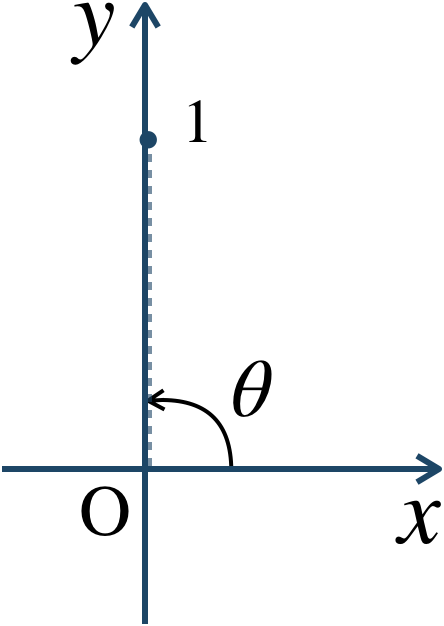
与えられた式を変形すると、$$~~~\frac{\,\beta-\alpha \,}{\,\gamma-\alpha \,}=i$$右辺の \(i\) を極形式で表すと、
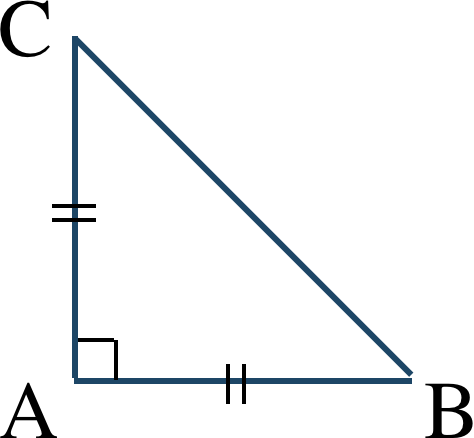
絶対値 \(1\) 、偏角 \({\large \frac{\,\pi\,}{\,2\,}}\) より、$$~~~i=\cos{\frac{\,\pi \,}{\,2 \,}}+i\sin{\frac{\,\pi \,}{\, 2\,}}$$よって、絶対値の条件より、$$~~~\left|\frac{\,\beta-\alpha \,}{\,\gamma-\alpha \,}\right|={\rm \frac{\, AB\,}{\,AC \,}}=1$$これより、$$~~~{\rm AB=AC}~~~\cdots~{\large ①}$$また、角の条件より、$$~~~\arg \left(\frac{\,\beta-\alpha \,}{\,\gamma-\alpha \,}\right)=\angle {\rm CAB}=\theta$$よって、$$~~~\angle{\rm CAB}=\frac{\,\pi \,}{\,2 \,}~~~\cdots~{\large ②}$$①と②より、\(\triangle {\rm ABC}\) を図で表すと、
したがって、\(\triangle {\rm ABC}\) は \(\angle{\rm CAB}={\large \frac{\,\pi\,}{\,2\,}}\) 、\({\rm AB=AC}\) の直角二等辺三角形となる。
問題解説(2)
与えられた式を変形すると、$$~~~\frac{\,\alpha-\beta \,}{\,\gamma-\beta \,}=1+\sqrt{3}i$$右辺の \(1+\sqrt{3}i\) を極形式で表すと、絶対値は、$$~~~~~~\left|1+\sqrt{3}i\right|$$$$~=\sqrt{1^2+(\sqrt{3})^2}$$$$~=\sqrt{1+3}=\sqrt{4}=2$$また、複素数平面上に表すと、
偏角は、\(\theta={\large \frac{\,\pi\,}{\,3\,}}\)
これより、$$~~~2\left(\cos{\frac{\,\pi \,}{\,3 \,}}+i\sin{\frac{\,\pi \,}{\,3 \,}}\right)$$よって、絶対値の条件より、$$~~~\left|\frac{\,\alpha-\beta \,}{\,\gamma-\beta \,}\right|={\rm \frac{\, BA\,}{\,BC \,}}=2$$これより、$$~~~{\rm BA\,:\,BC}=2\,:\,1~~~\cdots~{\large ①}$$また、角の条件より、$$~~~\arg \left(\frac{\,\alpha-\beta \,}{\,\gamma-\beta \,}\right)=\angle {\rm CBA}=\theta$$よって、$$~~~\angle{\rm CBA}=\frac{\,\pi \,}{\,3\,}~~~\cdots~{\large ②}$$①と②より、\(\triangle {\rm ABC}\) を図で表すと、
よって、\(1\,:\,2\,:\,\sqrt{3}\) の直角三角形となる。
したがって、$$~~~{\rm BC\,:\,BA\,:\,AC}=1\,:\,2\,:\,\sqrt{3}$$$$~~~\angle{\rm A}=\frac{\,\pi \,}{\,6 \,}~,~\angle{\rm B}=\frac{\,\pi \,}{\,3 \,}~,~\angle{\rm C}=\frac{\,\pi \,}{\,2 \,}$$の直角三角形となる。
今回のまとめ
複素数平面上の三角形の形状の求め方について解説しました。。与えられた式の右辺を極形式で表し、絶対値と偏角からどのような三角形となるか読み取りましょう。