順列と組合せ

2018.03.162020.06.09

順列と組合せの使い分け
問題解説：順列と組合せ
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

順列と組合せの使い分け

Point：順列と組合せ・順列
問題(1)は３つの文字を選んで、しかも一列に並べています。これは選んだ３つの文字に順位を付けているイメージです。

これで１通りとなります。ここで大事なのは

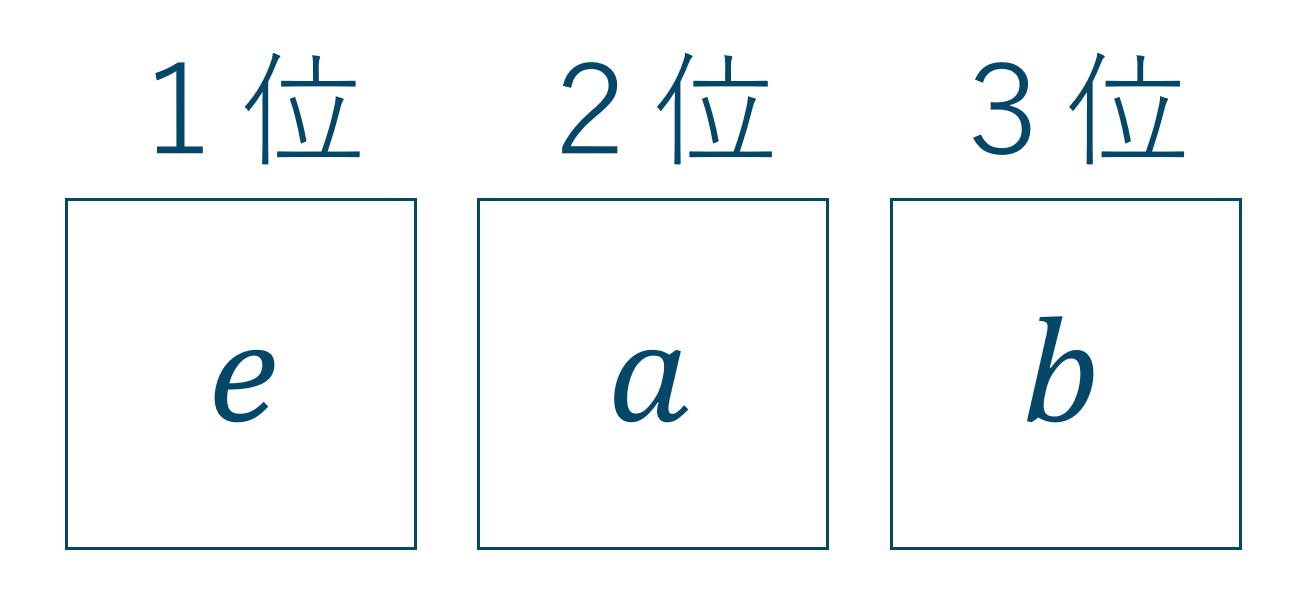
このように順位が変わったらたとえ選んだ種類が同じであってもまったく別の通りとなります。
これが「順列」の考え方です。

・組合せ
問題(2)では選ぶだけです。これはただ文字を３つ選んでいるだけです。

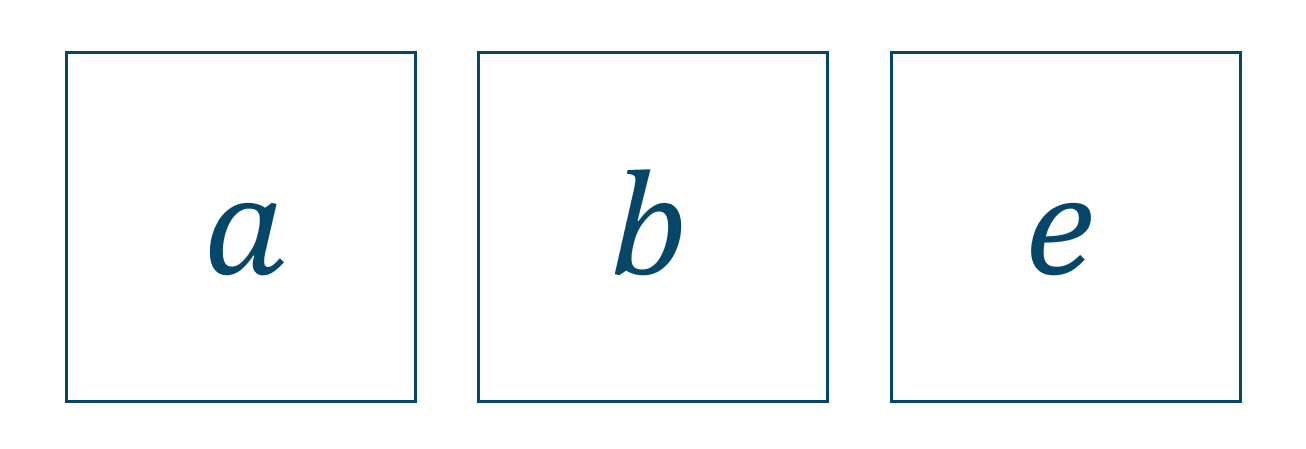
これが「組合せ」の考え方です。

この「順位を付けるかどうか」が順列と組合せの重要な違いとなります、

問題解説：順列と組合せ

問題解説(1)

問題 $a,b,c,d,e$ の５つの文字がそれぞれ１つずつあるとき、次の問いに答えよ。
${\small (1)}~$３つの文字を選び一列に並べるときの場合の数

(1)は、５つの文字から３つの文字を選んで、順位を付けているので順列となります。
１位、２位、３位と順位を付けるので、

とそれぞれの箱を描き、１位から順に何通りあるか箱の中に書いていきましょう。
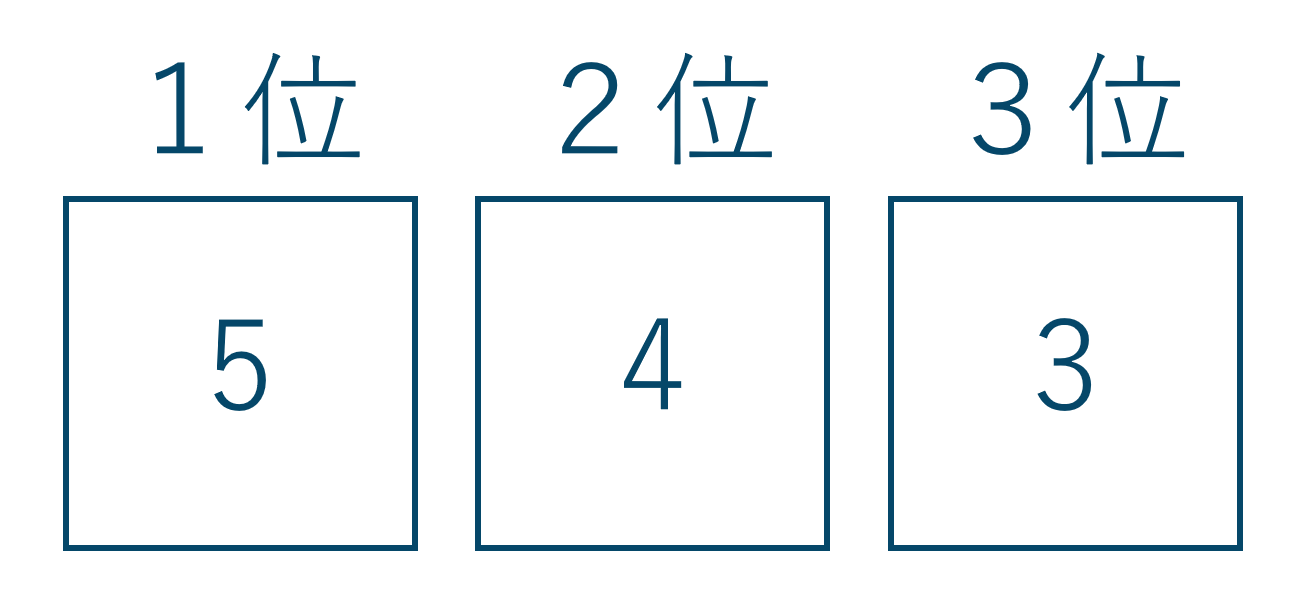
１位には５種類の文字のうちどれか１つが入るので５通りです。
２位では「１位と決めた文字」以外の４種類の文字から選ぶので４通り。
３位も同様に３通りとなります。

ここで、この順列では１位から順に「連続して」選んでいったので積の法則を使います。$$~~~5 \times 4 \times 3 =60$$よって、答えは60通りとなります。

問題解説(2)

問題 $a,b,c,d,e$ の５つの文字がそれぞれ１つずつあるとき、次の問いに答えよ。
${\small (2)}~$３つの文字を選ぶときの場合の数

５つのものから３つ選ぶ組合せより、記号 $\rm C$ を用いて、
　分子は $5$ から３つのかけ算
　分母は $3$ から３つのかけ算
よって、$$~~~{}_{5}{\rm C}_{3}=\frac{5\cdot 4\cdot 3}{3\cdot 2\cdot 1}$$$$~~~~~~~~~=5 \cdot 2$$$$~~~~~~~~~=10$$答えは $10$ となります。