中点連結定理と平行線と比

問題次の問いに答えよ。
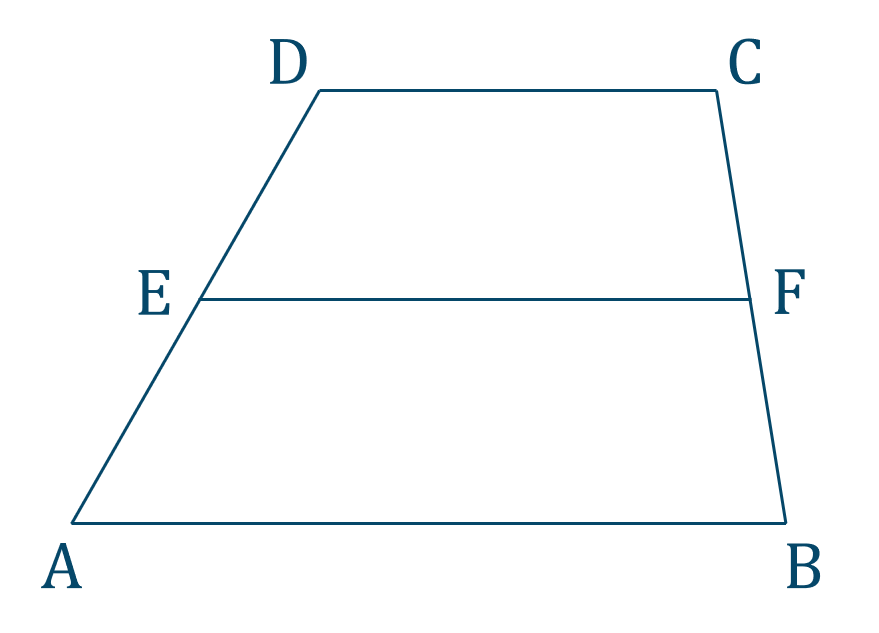
\({\small (1)}\) 次の台形 \({\rm ABCD}\) が \({\rm AB}\parallel{\rm DC}\) \(,\) \({\rm AB}=13\) \(,\) \({\rm CD}=7\) であり、点 \({\rm E~,~F}\) がそれぞれ \({\rm AD~,~BC}\) の中点とし、\({\rm AB}\parallel{\rm EF}\) であるとき、\({\rm EF}\) の長さを求めよ。

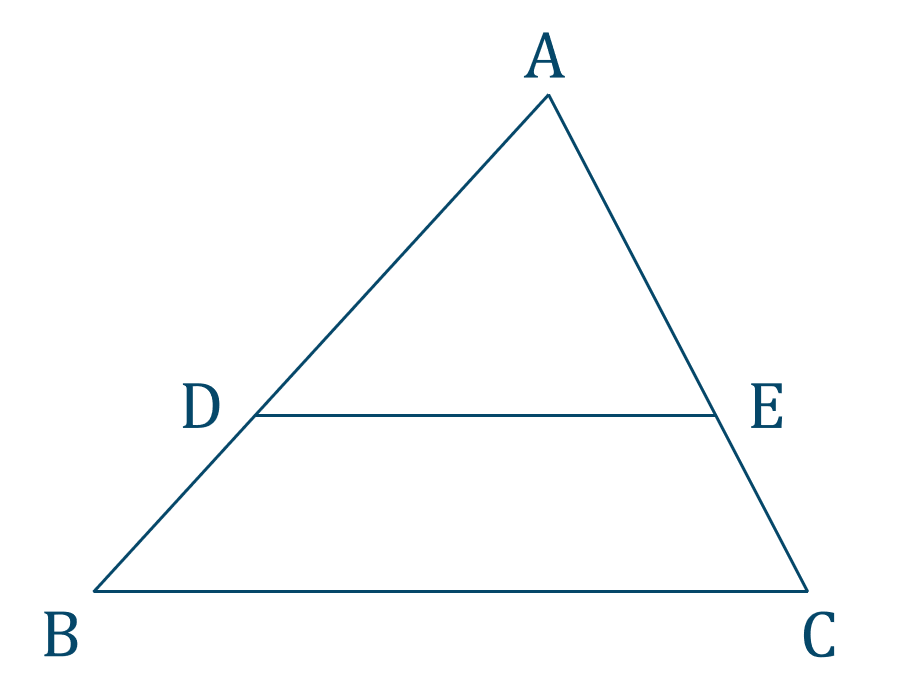
\({\small (2)}\) 次の \(\triangle {\rm ABC}\) について、\({\rm BC}\parallel{\rm DE}\) \(,\) \({\rm AD}=3\) \(,\) \({\rm DB}=2\) \(,\) \({\rm AE}=2\) \(,\) \({\rm BC}=6\) のとき、\({\rm EC}\) と \({\rm DE}\) の長さを求めよ。