三角形の外心の性質
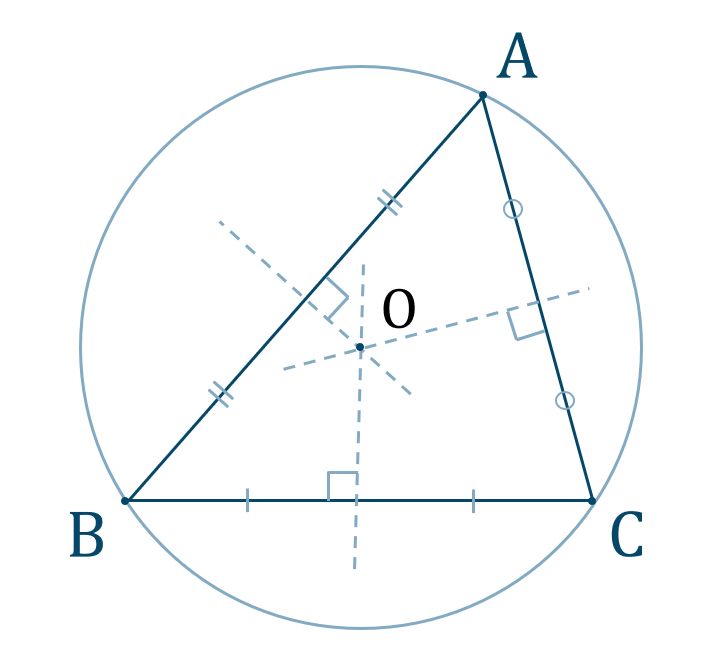
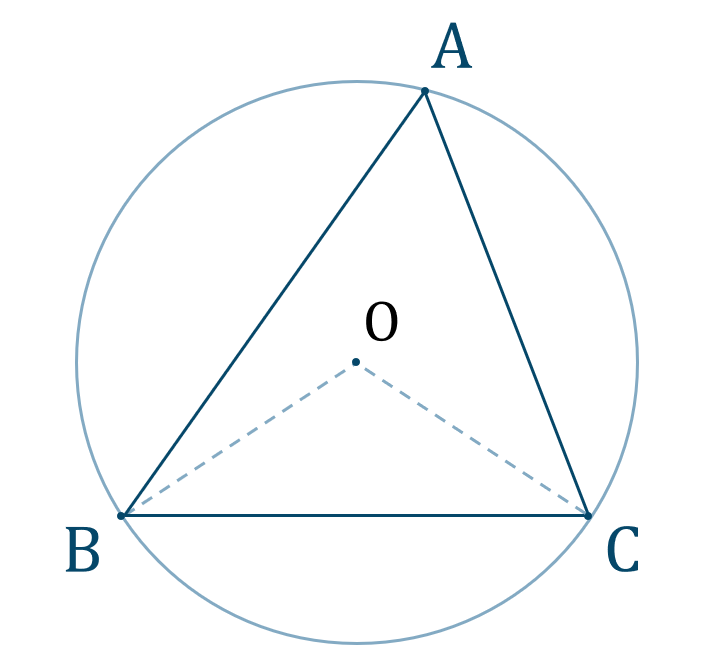
このときの交点 \({\rm O}\) を中心とする円を \(\triangle {\rm ABC}\) の外接円といい、点 \({\rm O}\) を外心という。
・外心についての性質
( ⅰ ) 円周角と中心角の定理が成り立つ
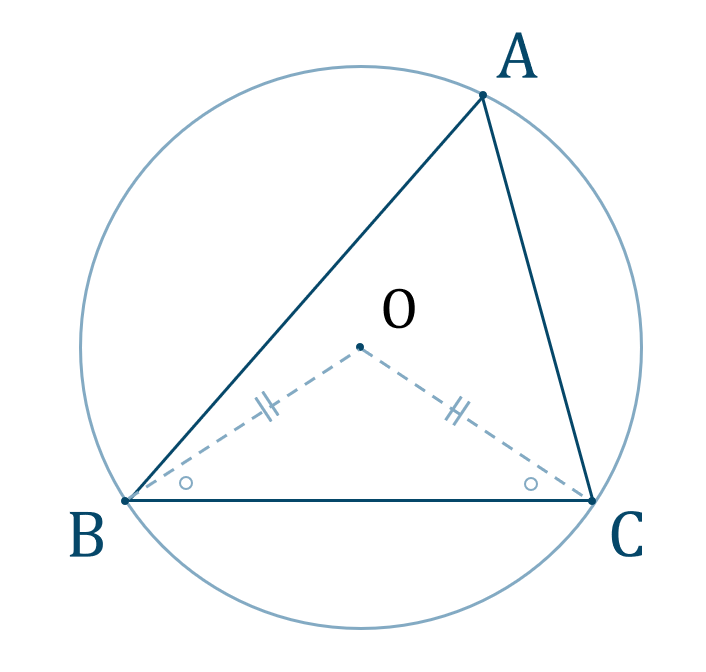
( ⅱ ) 外心 \({\rm O}\) から頂点に引いた線分は半径となるので、
これより、\(\triangle {\rm OBC}\) は二等辺三角形となります。よって、底角が等しくなるので、
問題解説：三角形の外心
問題解説(1)
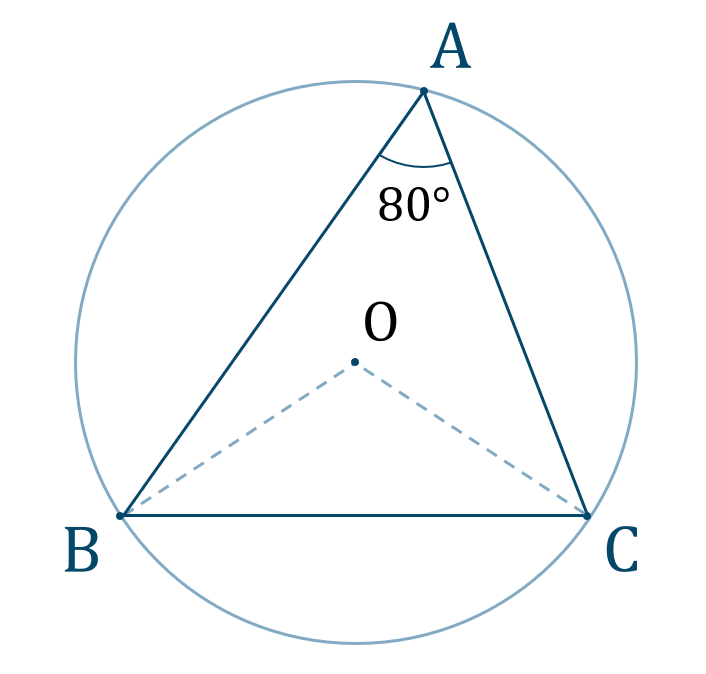
$${\small (1)}~\angle{\rm BOC}$$
図は次のようになります。
円周角と中心角の定理より、$$\hspace{ 10 pt}\angle{\rm BOC}=2\angle{\rm BAC}$$よって、値を代入すると、$$\hspace{ 10 pt}\angle{\rm BOC}=2\times80^\circ$$$$\hspace{ 42 pt}=160^\circ$$
よって、答えは$$~~~\angle{\rm BOC}=160^\circ$$となります。
問題解説(2)
次に \(\triangle {\rm OBC}\) は \({\rm OB}={\rm OC}\) の二等辺三角形となり、底角が等しくなるので、
$$~~~\angle{\rm OBC}=\angle{\rm OCB}$$また、三角形の内角の和より、$$~~~\angle{\rm BOC}+\angle{\rm OBC}+\angle{\rm OCB}=180^\circ$$値を代入すると、$$\hspace{ 10 pt}160^\circ+\angle{\rm OCB}+\angle{\rm OCB}=180^\circ$$移項すると$$\hspace{ 10 pt}2\angle{\rm OCB}=180^\circ-160^\circ$$$$\hspace{ 10 pt} 2\angle{\rm OCB}=20^\circ$$両辺を \(2\) で割ると、$$\hspace{ 10 pt}\angle{\rm OCB}=10^\circ$$
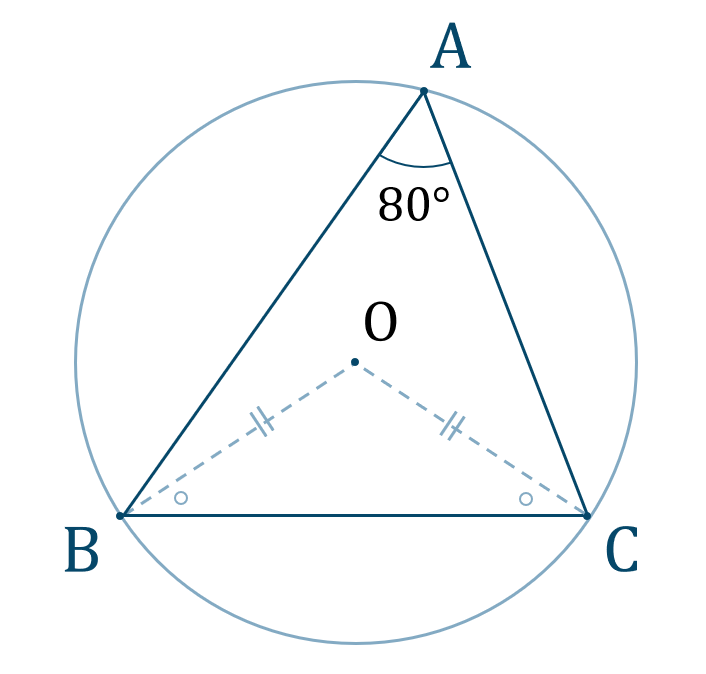
よって、答えは$$~~~\angle{\rm OCB}=10^\circ$$となります。
今回のまとめ
三角形の外接円とその中心の外心については、円周角と中心角の定理と半径より二等辺三角形ができることに注意して問題を解いていきましょう。
