三角形の垂心の性質
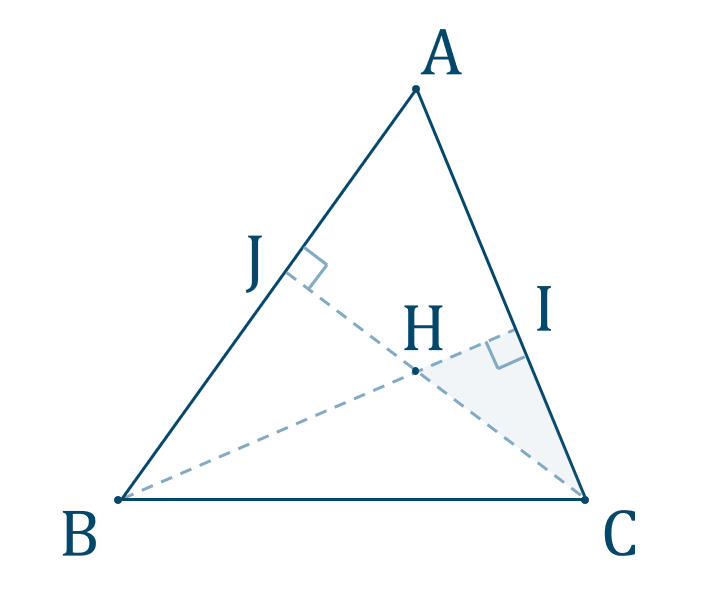
Point:三角形の垂心【定理】三角形の3つの頂点から対辺に下ろした垂線は1点で交わる。

このとき、交点 \({\rm H}\) を三角形の垂心といいます。
また、垂線を3本引くので \(\triangle {\rm ABC}\) の内部で複数の直角三角形ができます。これらを用いて問題を解きましょう。
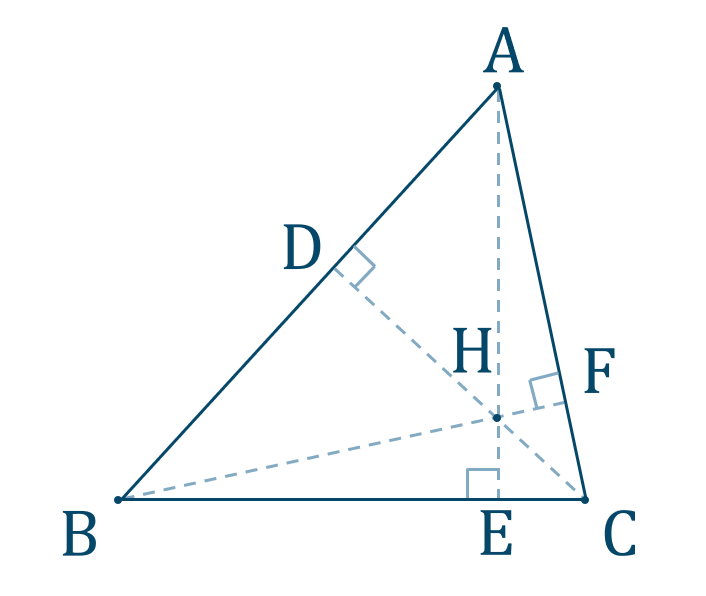
このとき、交点 \({\rm H}\) を三角形の垂心といいます。
また、垂線を3本引くので \(\triangle {\rm ABC}\) の内部で複数の直角三角形ができます。これらを用いて問題を解きましょう。
問題解説:三角形の垂心
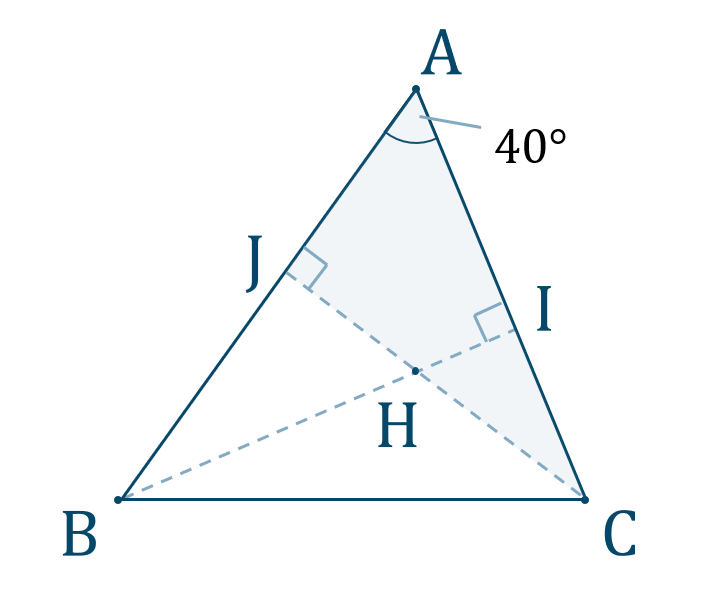
問題次の図で \(\angle{\rm A}=40^\circ\) である鋭角三角形 \({\rm ABC}\) の垂心を \({\rm H}\) とするとき、\(\angle{\rm BHC}\) の値を求めよ。

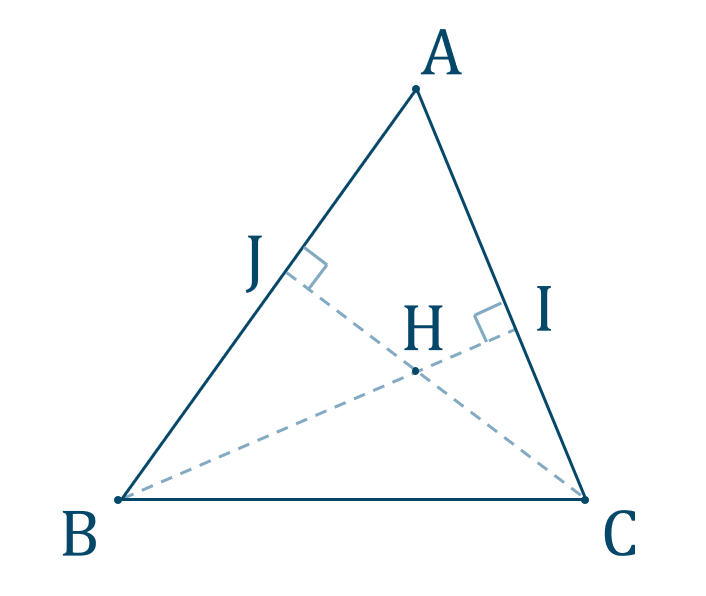
図は次のようになります。
\(\triangle {\rm AJC}\) において、直角三角形であることより、$$\hspace{ 10 pt}\angle{\rm JAC}+\angle{\rm ACJ}=90^\circ$$\(\angle{\rm JAC}=40^\circ\) より、$$\hspace{ 10 pt}40^\circ+\angle{\rm ACJ}=90^\circ$$移項すると、$$\hspace{ 10 pt}\angle{\rm ACJ}=90^\circ-40^\circ$$$$\hspace{ 40 pt}=50^\circ$$
次に、\(\triangle {\rm CHI}\) とその外角 \(\angle{\rm BHC}\) において、
外角は三角形の他の内角の和と等しくなるので、$$\hspace{ 10 pt}\angle{\rm BHC}=\angle{\rm HIC}+\angle{\rm ICH}$$ここで、$$~~~\angle{\rm HIC}=90^\circ~,~\angle{\rm ICH}=\angle{\rm ACJ}=50^\circ$$これらを用いると、$$\hspace{ 10 pt}\angle{\rm BHC}=90^\circ+50^\circ$$$$\hspace{ 42 pt}=140^\circ$$
よって、答えは$$~~~\angle{\rm BHC}=140^\circ$$となります。
今回のまとめ
三角形の垂心についての問題は、垂線を引いたときの直角三角形に着目して解いていきましょう。

【問題一覧】数学A:図形の性質
このページは「高校数学A:図形の性質」の問題一覧ページとなります。解説の見たい単元名がわからないとき...