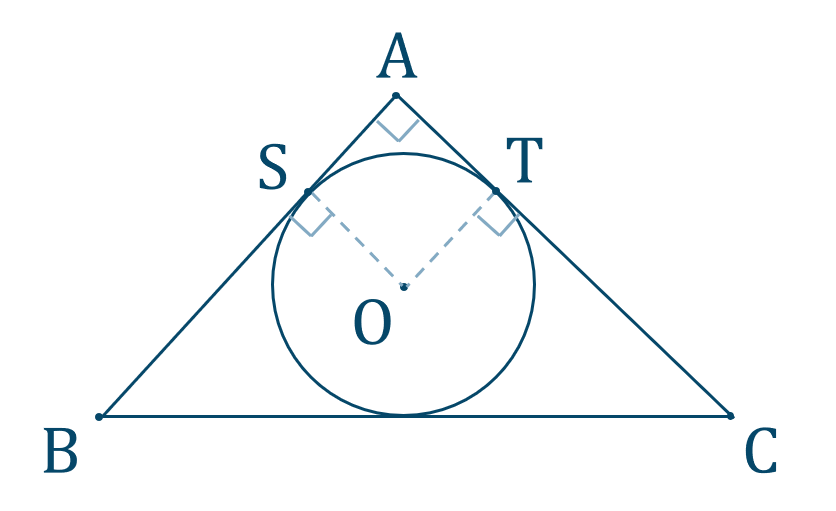
内接円と接線の条件
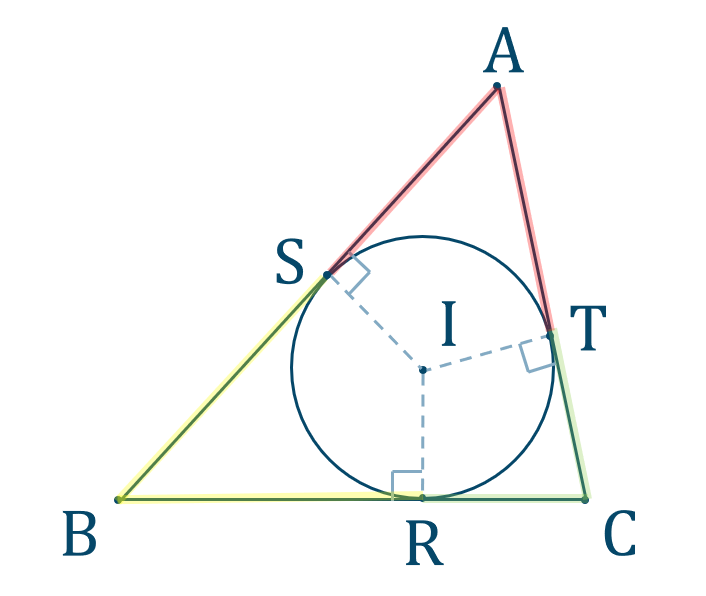
円と接線の性質より、
が成り立ちます。また、他の頂点でも同様に成り立ちます。
また、次のように \(\angle{\rm SAT}=90^\circ\) であるとき、
円より、四角形 \({\rm ASOT}\) は正方形となります。よって、
となり、円の半径と等しくなります。
問題解説：内接円と接線の条件
問題解説(1)
\({\small (1)}\) \({\rm BC}\) の長さを求めよ。
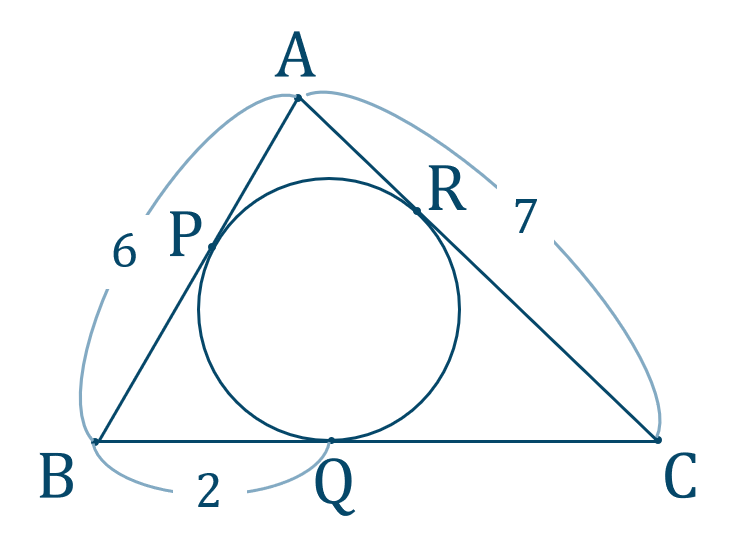
点 \({\rm B}\) での円と接線の条件より、
$$\hspace{ 10 pt}{\rm BQ}={\rm BP}=2$$また、$$\hspace{ 10 pt}{\rm AP}={\rm AB}-{\rm BP}$$$$\hspace{ 27 pt}=6-2$$$$\hspace{ 27 pt}=4$$
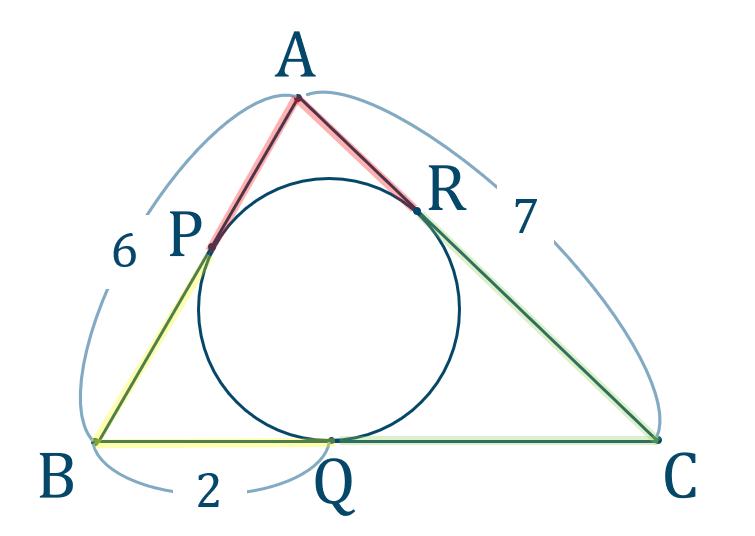
次に、点 \({\rm A}\) での円と接線の条件より、$$\hspace{ 10 pt}{\rm AP}={\rm AR}=4$$また、$$\hspace{ 10 pt}{\rm CR}={\rm AC}-{\rm AR}$$$$\hspace{ 27 pt}=7-4$$$$\hspace{ 27 pt}=3$$
次に、点 \({\rm C}\) での円と接線の条件より、$$\hspace{ 10 pt}{\rm CR}={\rm CQ}=3$$また、$$\hspace{ 10 pt}{\rm BC}={\rm BQ}+{\rm CQ}$$$$\hspace{ 27 pt}=2+3$$$$\hspace{ 27 pt}=5$$
よって、答えは$$~~~{\rm BC}=5$$となります。
問題解説(2)
\({\small (2)}\) 内接円の半径 \(r\) を求めよ。
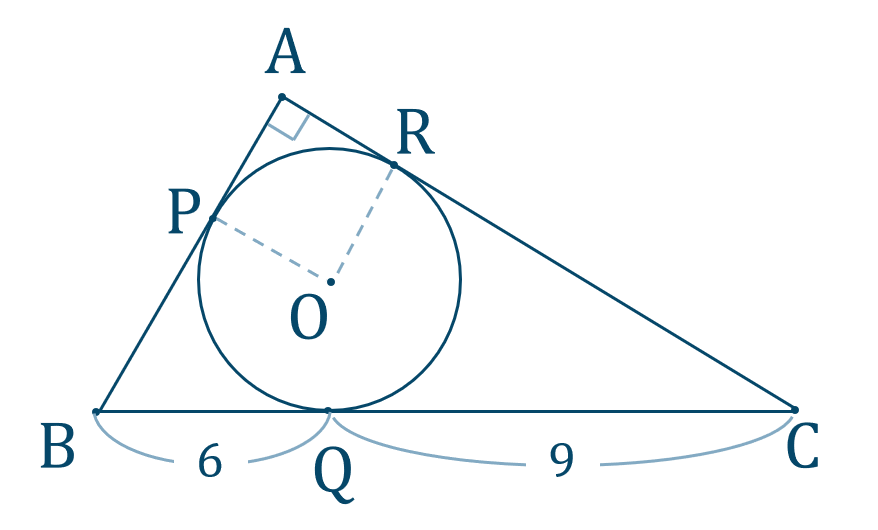
点 \({\rm A}\) について、\(\angle{\rm A}=90^\circ\) で円と接線の条件より、
$$~~~{\rm AP}={\rm AR}={\rm OP}={\rm OR}=r$$
また、点 \({\rm B}\) での円と接線の条件より、$$~~~{\rm BP}={\rm BQ}=6$$
また、点 \({\rm C}\) での円と接線の条件より、$$~~~{\rm CQ}={\rm CR}=9$$
これらより、$$~~~{\rm AB}=r+6$$$$~~~{\rm BC}=6+9=15$$$$~~~{\rm AC}=r+9$$
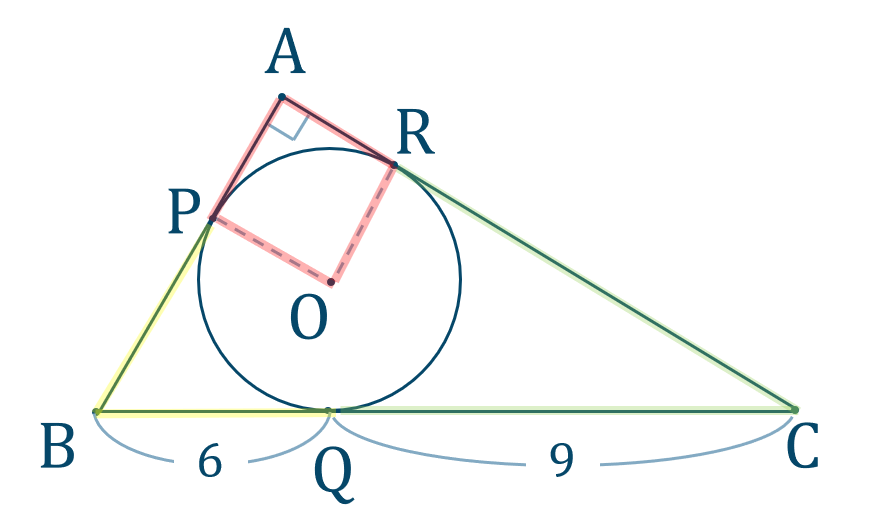
ここで、\(\triangle {\rm ABC}\) は直角三角形であるので、三平方の定理より、$$~~~{\rm AB}^2+{\rm AC}^2={\rm BC}^2$$値を代入すると、$$\hspace{ 10 pt}(r+6)^2+(r+9)^2=15^2$$展開すると、$$\hspace{ 10 pt}r^2+12r+36+r^2+18r+81=225$$移項すると、$$\hspace{ 10 pt}2r^2+30r+117-225=0$$$$\hspace{ 36 pt}2r^2+30r-108=0$$両辺を \(2\) で割ると、$$\hspace{ 10 pt}r^2+15r-54=0$$左辺を因数分解すると、$$\hspace{ 10 pt}(r+18)(r-3)=0$$\(r>0\) より、答えは$$~~~r=3$$となります。
今回のまとめ
内接円と接線の条件を用いて、等しい線分を図示しながら問題を解いていきましょう。また、(2)のような図形では半径と線分が等しくなり、直角三角形となるので三平方の定理を用いて計算しましょう。
