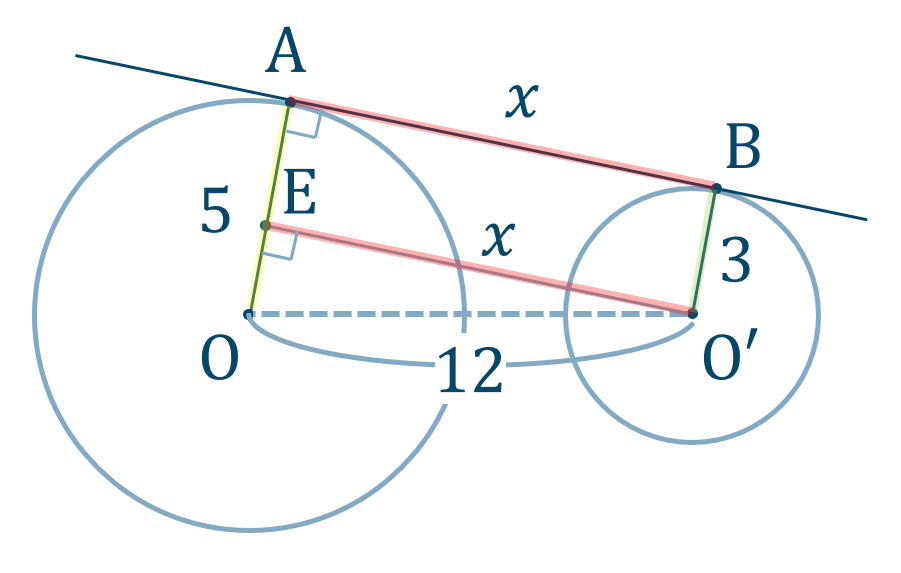
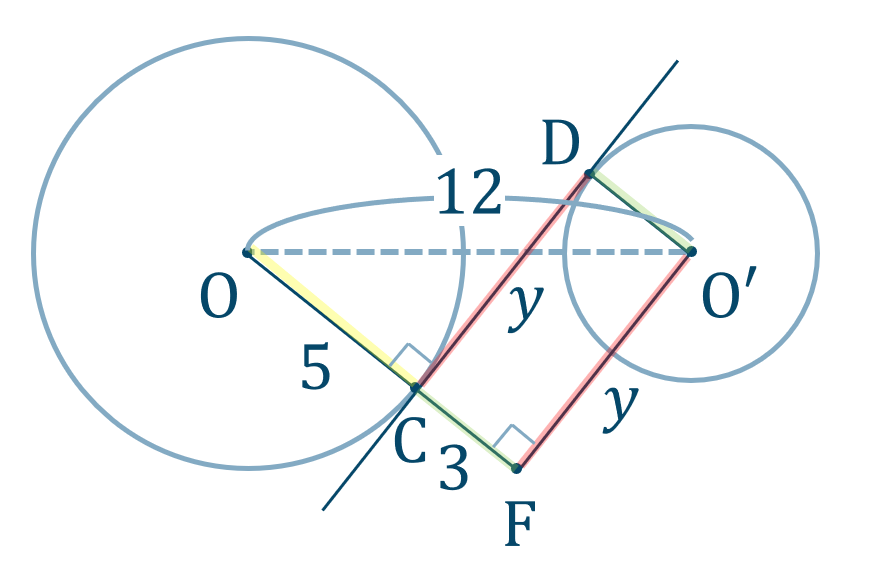
共通接線の長さ
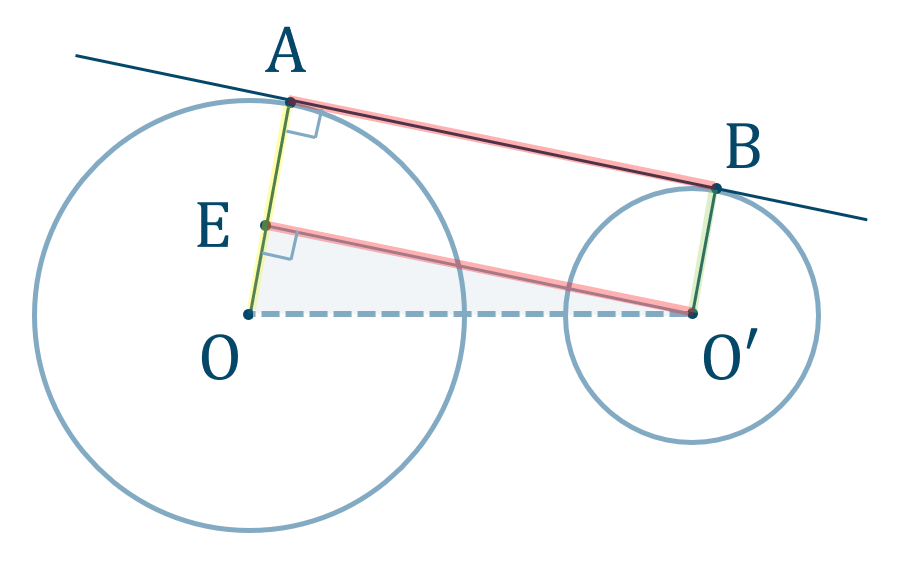
\({\rm AB}\) を平行移動して、\(\triangle {\rm OO’E}\) で三平方の定理を用いる。
パターン(2)
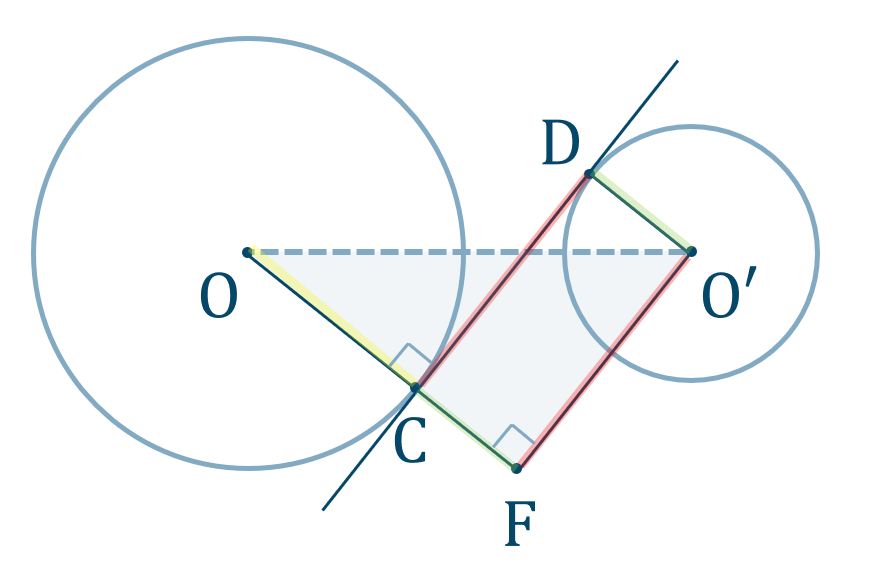
\({\rm CD}\) を平行移動して、\(\triangle {\rm OO’F}\) で三平方の定理を用いる。
問題解説:共通接線の長さ
問題解説(1)
\({\small (1)}\) 共通接線 \({\rm AB}\) の線分の長さ
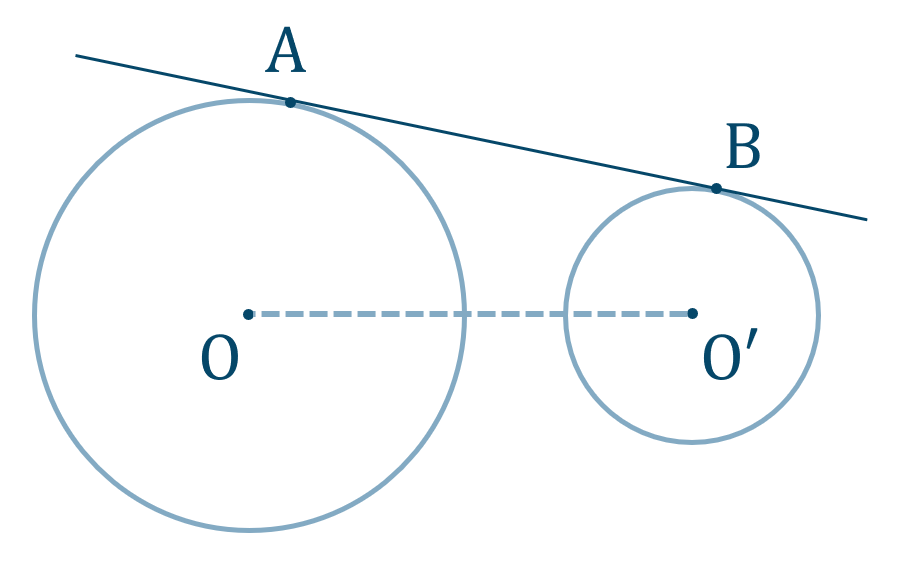
線分 \({\rm AB}\) の長さを \(x\) とし、線分 \({\rm AB}\) を点 \({\rm O’}\) まで平行移動した線分を \({\rm EO’}\) とすると、図は次のようになります。
ここで、半径 \(3\) より、$$~~~{\rm AE}={\rm BO’}=3$$よって、$$\hspace{ 10 pt}{\rm OE}={\rm AO}-{\rm AE}$$$$\hspace{ 27 pt}=5-3$$$$\hspace{ 27 pt}=2$$
次に \(\triangle {\rm OO’E}\) について、三平方の定理を用いると、$$\hspace{ 10 pt}12^2=2^2+x^2$$両辺を入れ替えて、移項すると、$$\hspace{ 10 pt}x^2+4=144$$$$\hspace{ 10 pt}x^2=144-4$$$$\hspace{ 10 pt}x^2=140$$\(x>0\) より、$$\hspace{ 10 pt}x=\sqrt{140}$$$$\hspace{ 19 pt}=2\sqrt{35}$$
よって、答えは$$~~~{\rm AB}=2\sqrt{35}$$となります。
問題解説(2)
\({\small (2)}\) 共通接線 \({\rm CD}\) の線分の長さ

線分 \({\rm CD}\) の長さを \(y\) とし、線分 \({\rm CD}\) を点 \({\rm O’}\) まで平行移動した線分を \({\rm FO’}\) とすると、図は次のようになります。
ここで、半径 \(3\) より、$$~~~{\rm CF}={\rm O’D}=3$$よって、$$\hspace{ 10 pt}{\rm OF}={\rm OC}+{\rm OF}$$$$\hspace{ 27 pt}=5+3$$$$\hspace{ 27 pt}=8$$
次に \(\triangle {\rm OO’F}\) について、三平方の定理を用いると、$$\hspace{ 10 pt}12^2=8^2+y^2$$両辺を入れ替えて、移項すると、$$\hspace{ 10 pt}y^2+64=144$$$$\hspace{ 33 pt}y^2=144-64$$$$\hspace{ 33 pt}y^2=80$$\(y>0\) より、$$\hspace{ 10 pt}y=\sqrt{80}$$$$\hspace{ 18 pt}=4\sqrt{5}$$
よって、答えは$$~~~{\rm CD}=4\sqrt{5}$$となります。
今回のまとめ
共通接線の長さの問題では、線分を平行移動することで直角三角形をつくるようにしましょう。