内分点と外分点の作図

2018.10.182020.06.09

問題解説：内分点と外分点の作図
1. 問題解説(1)
2. 問題解説(2)
今回のまとめ

問題解説：内分点と外分点の作図

問題解説(1)

問題次の図形を作図せよ。
\({\small (1)}\) 線分 \({\rm AB}\) を \(1:3\) に内分する点

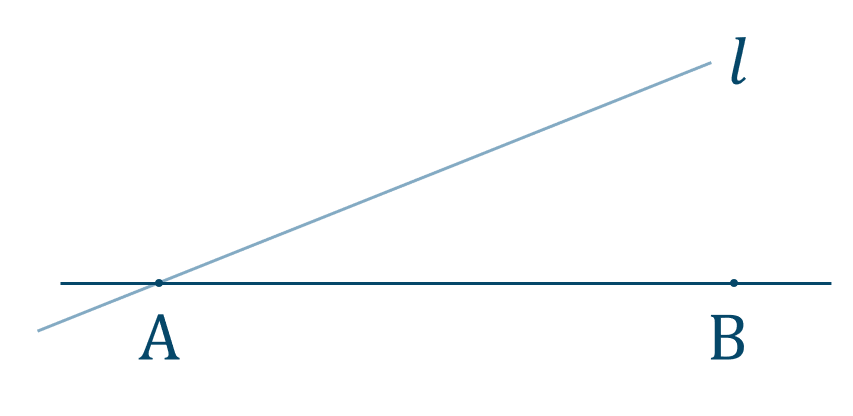
点 \({\rm A}\) を通り直線 \({\rm AB}\) とは別の直線 \(l\) を引きます。

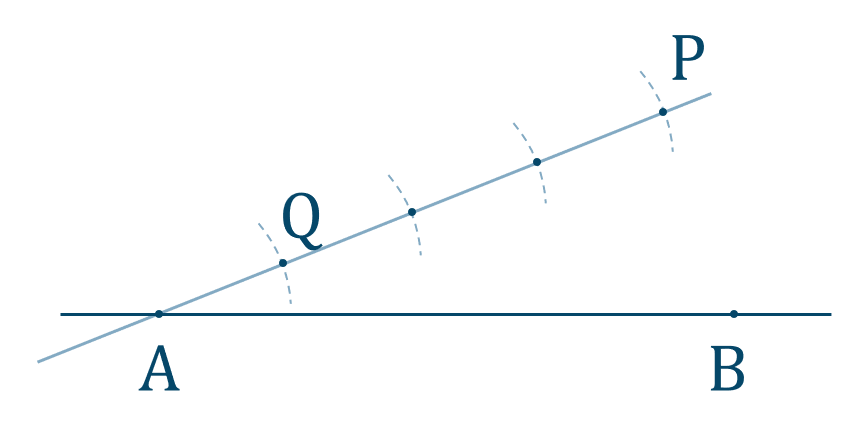
直線 \(l\) に点 \({\rm A}\) からコンパスで等間隔に４点をとります。（比が \(1:3\) より、\(1+3=4\) 点必要となります。）
この４点を \(1:3\) に内分する点を \({\rm Q}\) として、４点目を \({\rm P}\) とします。

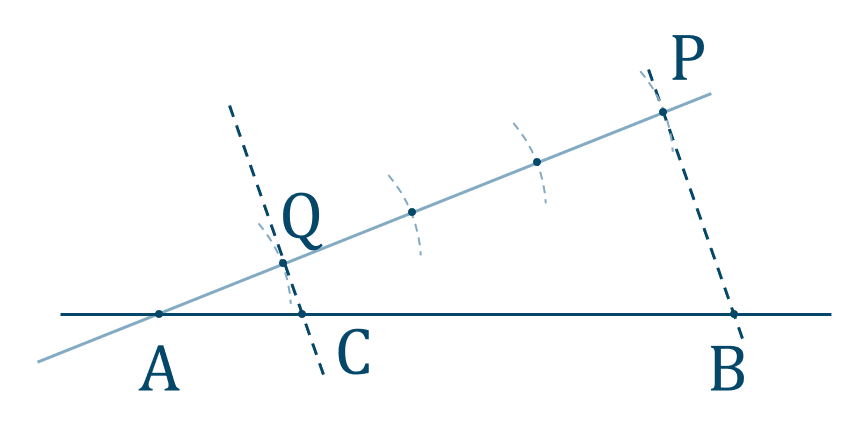
直線 \({\rm PB}\) を引きこの直線に平行で点 \({\rm Q}\) を通る直線を引きます。

このとき、線分 \({\rm AB}\) との交点 \({\rm C}\) が線分 \({\rm AB}\) を \(1:3\) に内分する点となります。

問題解説(2)

問題次の図形を作図せよ。
\({\small (2)}\) 線分 \({\rm AB}\) を \(3:1\) に外分する点

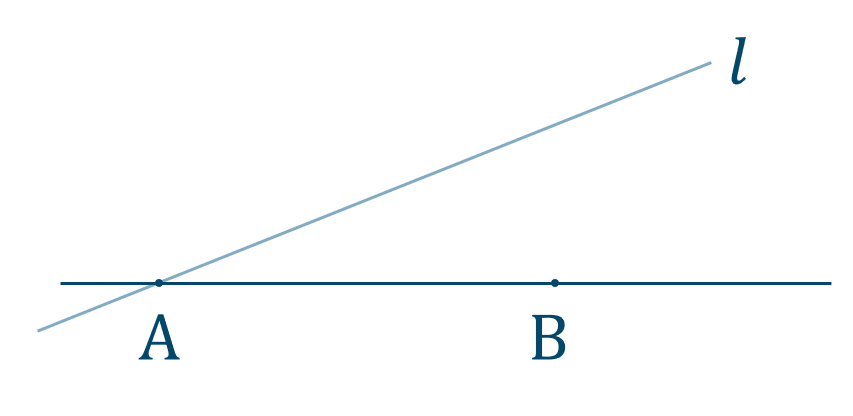
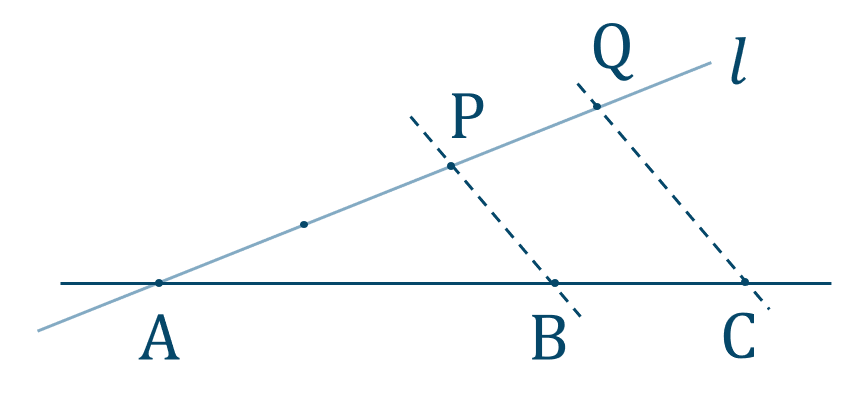
点 \({\rm A}\) を通り直線 \({\rm AB}\) とは別の直線 \(l\) を引きます。

直線 \(l\) に点 \({\rm A}\) からコンパスで等間隔に３点をとります。（外分点のときは、大きい比の値の分だけ必要です。）
２点目を \({\rm P}\) 、３点目を \({\rm Q}\) とします。

直線 \({\rm PB}\) を引きこの直線に平行で点 \({\rm Q}\) を通る直線を引きます。

このとき、線分 \({\rm AB}\) との交点 \({\rm C}\) が線分 \({\rm AB}\) を \(3:1\) に外分する点となります。