分数倍の作図

2018.10.182020.06.09

問題解説：分数倍の作図
今回のまとめ

問題解説：分数倍の作図

問題${\rm AB}$ の長さが $1$ のとき、${\rm AP}={\large \frac{3}{2}}$ となるような点 ${\rm P}$ を作図せよ。

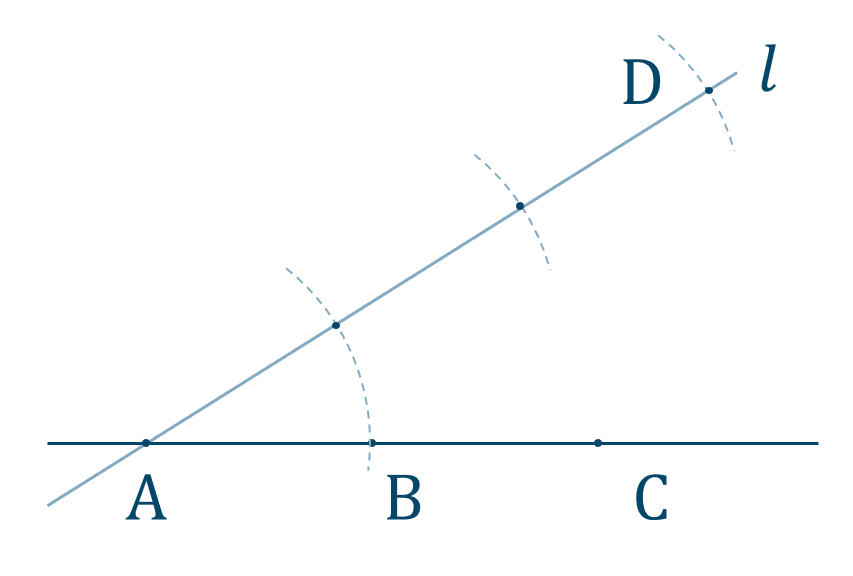
直線 ${\rm AB}$ 上に分母の値より、${\rm AC}=2$ となるようにコンパスを用いて点 ${\rm C}$ をとります。

点 ${\rm A}$ を通り直線 ${\rm AB}$ とは別の直線 $l$ を引き分子の値より ${\rm AD}=3$ となるような点 ${\rm D}$ をとります。

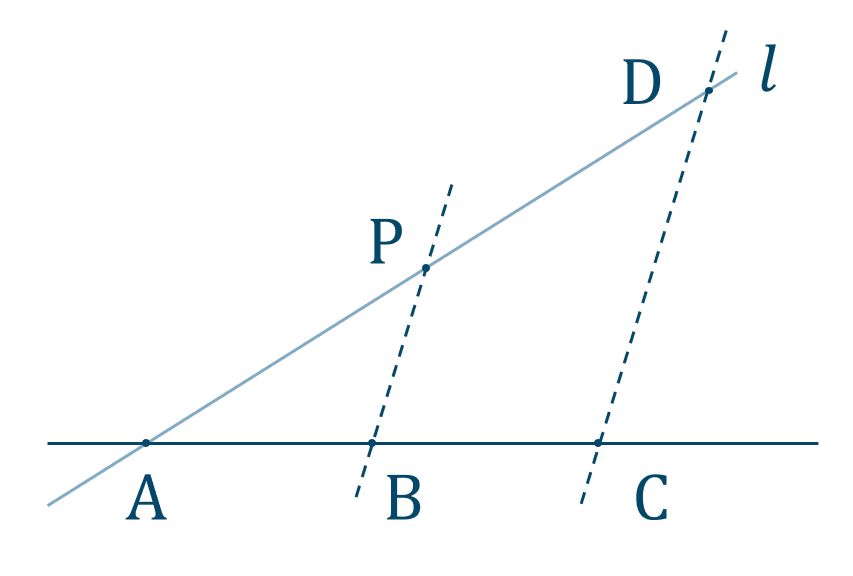
直線 ${\rm CD}$ を引いて、この直線に平行で点 ${\rm B}$ を通る直線を作図します。

このとき、直線 ${\rm AD}$ との交点を ${\rm D}$ とすると、$$~~~{\rm AP}=\frac{3}{2}$$となります。