図形と漸化式の解法
① \(n=1~,~2~,~3~,~4~,~\cdots\) と実際に図形を描いていき、\(n\) が増えると、どのように変化するかを推定します。
② \(n=k\) のときの \(a_k\) より、\(k+1\) 番目の図形の変化がどのようになるかを①より考えて、\(a_{k+1}\) との関係を式にします。
③ 立てた漸化式を解きます。
問題解説
\(n=1\) のとき、直線は１本となり交点はないので、
$$~~~a_1=0~~~\cdots{\Large ①}$$
\(n=2\) のとき、直線は２本となり交点が１つとなるので、
$$~~~a_2=1$$
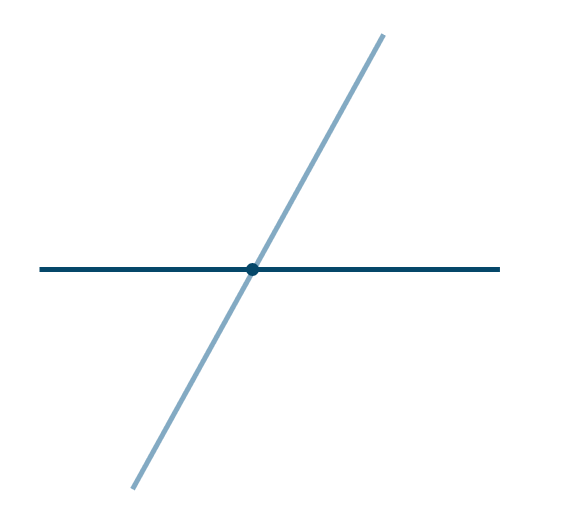
\(n=3\) のとき、直線は３本となり交点が２つ増えて３つとなるので、
$$~~~a_3=3$$
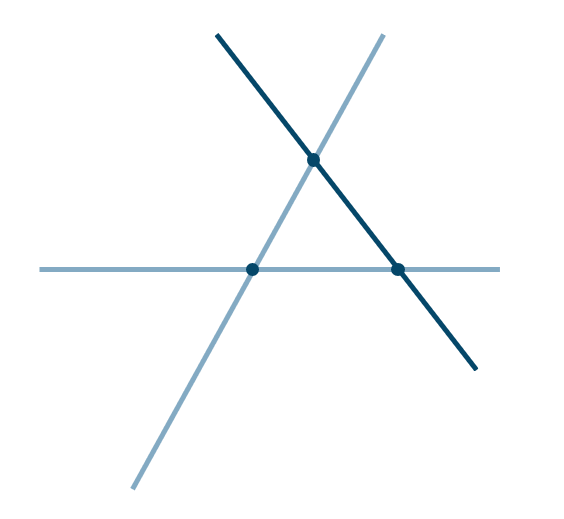
\(n=4\) のとき、直線は４本となり交点が３つ増えて６つとなるので、
$$~~~a_4=6$$
次に \(n=k\) のとき、\(k\) 本の直線があり \(a_k\) 個の交点があります。
ここで、\(k+1\) 本目の直線を引くと、もとの \(k\) 本の直線すべてと１点ずつで交わり、交点が \(k\) 個増えます。
よって、\(k+1\) 本の直線での交点の個数 \(a_{k+1}\) は、$$~~~a_{k+1}=a_k+k$$
この漸化式について、\(n≧2\) のとき、$$~~~a_{n+1}-a_n=n$$この数列の階差数列は、一般項が \(n\) となるので、$$\hspace{ 10 pt}a_n=a_1+\sum_{k=1}^{n-1}k$$$$\hspace{ 22 pt}=0+\frac{1}{2}(n-1)\{(n-1)+1\}$$$$\hspace{ 22 pt}=\frac{1}{2}(n-1)(n-1+1)$$$$\hspace{ 22 pt}=\frac{1}{2}(n-1)n$$$$\hspace{ 22 pt}=\frac{1}{2}n(n+1)$$ここで、この式は \(n=1\) のとき、$$\hspace{ 10 pt}a_1=\frac{1}{2}\cdot1\cdot(1-1)$$$$\hspace{ 21 pt}=\frac{1}{2}\cdot1\cdot0$$$$\hspace{ 21 pt}=0$$よって、①より \(n=1\) のときも成り立ちます。
よって、答えは$$~~~a_n=\frac{1}{2}n(n-1)$$となります。
今回のまとめ
図形と漸化式についての問題は、\(n=k\) のときと、\(n=k+1\) との変化を式にすることがポイントとなります。実際に \(n=1~,~2~,~3~,~\cdots\) のときより規則性を見つけましょう。
