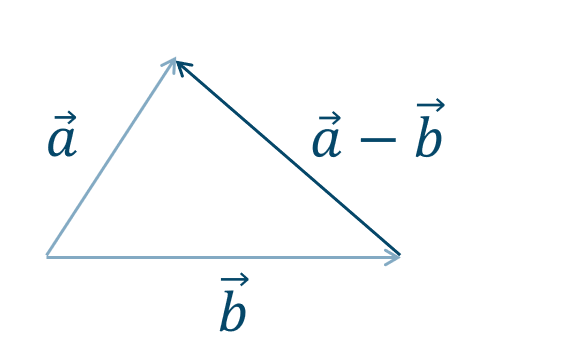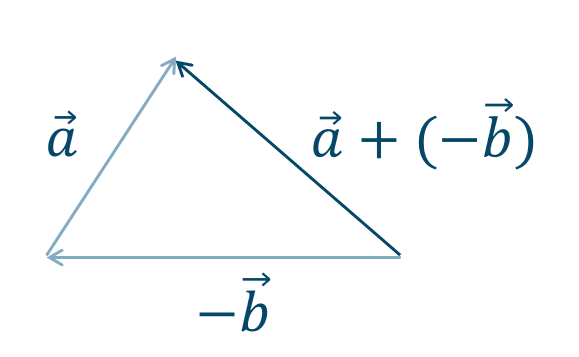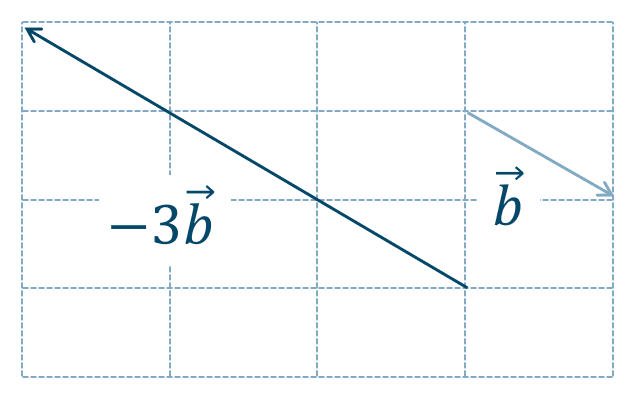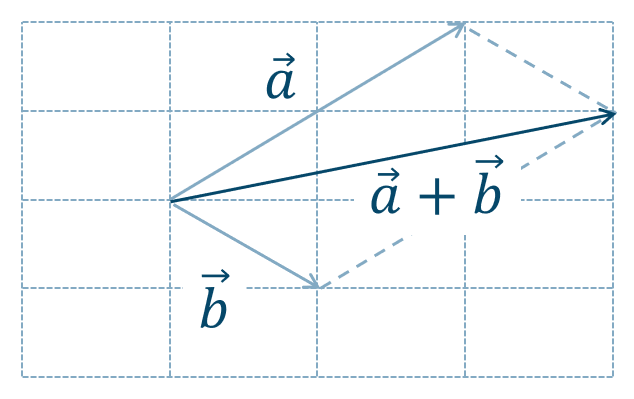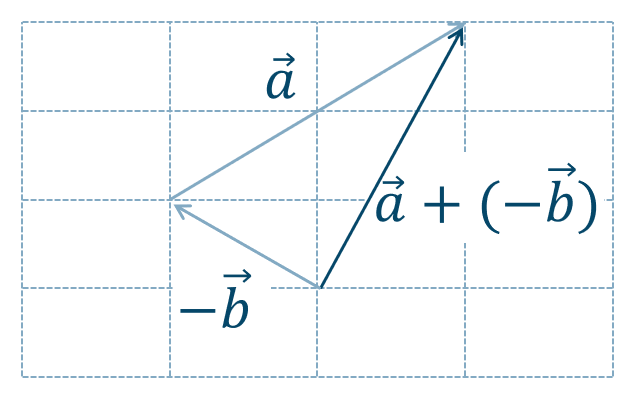ベクトルの実数倍・加法・減法
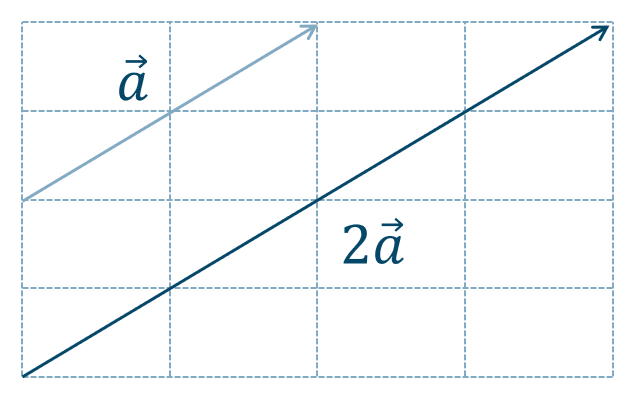
( ⅰ ) \(k>0\) のとき、
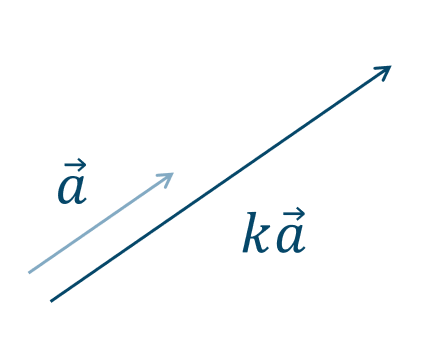
\(\overrightarrow{a}\) と同じ向きで、大きさが \(k\) 倍のベクトルとなります。
( ⅱ ) \(k=0\) のとき、$$~~~k\overrightarrow{a}=0\cdot\overrightarrow{a}=\overrightarrow{0}$$よって、零ベクトルとなります。
( ⅲ ) \(k<0\) のとき、
\(\overrightarrow{a}\) と反対の向きで、大きさが \(k\) 倍のベクトルとなります。
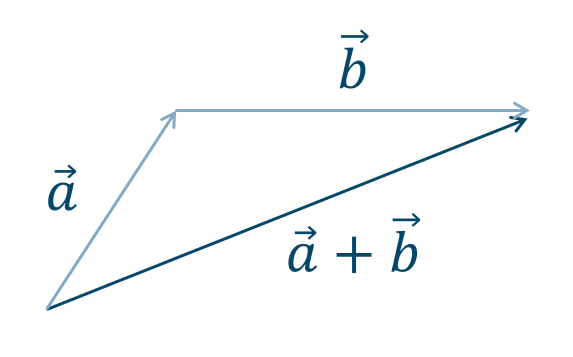
ベクトルの和 \(\overrightarrow{a}+\overrightarrow{b}\) は、
(1) \(\overrightarrow{a}\) の終点と \(\overrightarrow{b}\) の始点を一致させるように平行移動させて考えると次のようになります。
(2) ２つのベクトルの始点を一致させて平行四辺形を作り、その対角線のベクトルを考えると次のようになります。
ベクトルの差 \(\overrightarrow{a}-\overrightarrow{b}\) は、
(1) ２つのベクトルの始点を一致させて三角形を作り、その辺のベクトルと考えると次のようになります。
(2) 式を \(\overrightarrow{a}+(-\overrightarrow{b})\) と考えて、\(\overrightarrow{b}\) の逆ベクトルを用いると次のようになります。
問題解説：ベクトルの実数倍・加法・減法
問題解説(1)
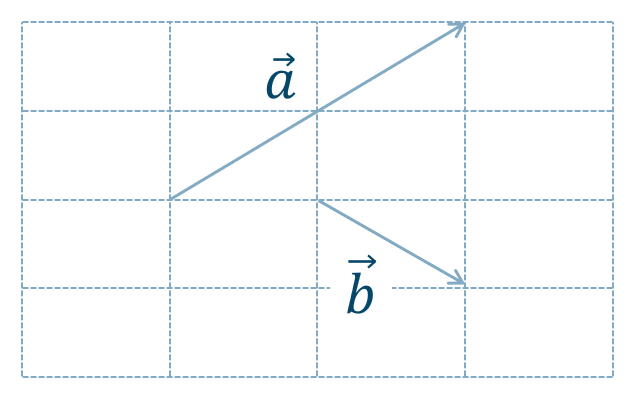$${\small (1)}~2\overrightarrow{a}$$
\(\overrightarrow{a}\) の大きさを \(2\) 倍にしたベクトルとなるので、答えは次の図のようになります。
問題解説(2)
\(\overrightarrow{b}\) の大きさを \(3\) 倍にして向きを反対にしたベクトルとなるので、答えは次の図のようになります。
問題解説(3)
\(\overrightarrow{a}\) の終点に \(\overrightarrow{b}\) の始点を一致させて考えると、答えは次のようになります。
【別解】２つのベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) の始点を一致させて平行四辺形を作り、その対角線のベクトルと考えると、答えは次のようになります。
問題解説(4)
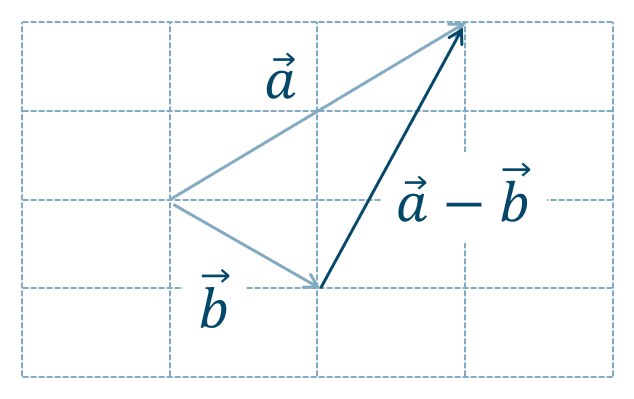
２つのベクトル \(\overrightarrow{a}~,~\overrightarrow{b}\) の始点を一致させて三角形を作り、その辺のベクトルと考えると、答えは次のようになります。
【別解】与えられた式を$$~~~\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{a}+(-\overrightarrow{b})$$として、\(\overrightarrow{b}\) の逆ベクトルを考えると、答えは次のようになります。
今回のまとめ
ベクトルの図示の方法はしっかりと覚えておきましょう。また、加法と減法に関してはそれぞれ２通りの表し方をおさえておきましょう。
