ベクトルの平行条件と単位ベクトル
これを満たす実数 \(k\) が存在します。
大きさが \(1\) のベクトル \(\overrightarrow{e}\) を単位ベクトルといいます。
例えば、\(\overrightarrow{a}\) と平行な単位ベクトルは \(\overrightarrow{a}\) の大きさが \(|\overrightarrow{a}|\) であることより、
となります。
問題解説:ベクトルの成分と平行条件
問題解説(1)
\({\small (1)}\) \(\overrightarrow{a}=(1~,~3)\) と平行な単位ベクトル \(\overrightarrow{e}\) を成分で表せ。
単位ベクトル \(\overrightarrow{e}\) の成分を、$$~~~\overrightarrow{e}=(x~,~y)$$とすると、
大きさが \(1\) であることより、$$\hspace{ 10 pt}|\overrightarrow{e}|=\sqrt{x^2+y^2}=1$$$$\hspace{ 51 pt}x^2+y^2=1~~~\cdots{\Large ①}$$
また、\(\overrightarrow{a}\neq\overrightarrow{0}~,~\overrightarrow{e}=\overrightarrow{0}\) で平行であるから実数 \(k\) を用いて、$$~~~\overrightarrow{e}=k\overrightarrow{a}$$よって、成分の計算をすると、$$\hspace{ 10 pt}\left(\begin{array} {c} x \\ y \end{array}\right)=k\left(\begin{array} {c} 1 \\ 3 \end{array}\right)$$$$\hspace{ 10 pt}\left(\begin{array} {c} x \\ y \end{array}\right)=\left(\begin{array} {c} k \\ 3k \end{array}\right)$$それぞれの成分は$$~~~\biggl\{ \begin{eqnarray} x=k \\ y=3k \end{eqnarray}$$これを①に代入すると、$$\hspace{ 10 pt}k^2+(3k)^2=1$$$$\hspace{ 22 pt}k^2+9k=1$$$$\hspace{ 35 pt}10k^2=1$$両辺を \(10\) で割ると、$$\hspace{ 10 pt}k^2=\frac{1}{10}$$よって、$$\hspace{ 10 pt}k=\pm\sqrt{\frac{1}{10}}$$$$\hspace{ 18 pt}=\pm\frac{\sqrt{1}}{\sqrt{10}}$$$$\hspace{ 18 pt}=\pm\frac{1}{\sqrt{10}}$$
よって、\(x=k~,~y=3k\) より、$$~~~x=\frac{1}{\sqrt{10}}~,~y=\frac{3}{\sqrt{10}}$$または、$$~~~x=-\frac{1}{\sqrt{10}}~,~y=-\frac{3}{\sqrt{10}}$$
よって、答えは$$~~~\overrightarrow{e}=\left( \frac{1}{\sqrt{10}}~,~\frac{3}{\sqrt{10}}\right)$$$$\hspace{ 32 pt}\left( -\frac{1}{\sqrt{10}}~,~-\frac{3}{\sqrt{10}}\right)$$となります。
問題解説(2)
\(\overrightarrow{b}\neq\overrightarrow{0}~,~\overrightarrow{c}\neq\overrightarrow{0}\) であることより、\(\overrightarrow{b}\) と \(\overrightarrow{c}\) が平行になるためには、$$~~~\overrightarrow{c}=k\overrightarrow{b}$$となる実数 \(k\) が存在します。
よって、成分の計算をすると、$$\hspace{ 10 pt}\left(\begin{array} {c} -1 \\ x-3 \end{array}\right)=k\left(\begin{array} {c} x \\ 2 \end{array}\right)$$$$\hspace{ 10 pt}\left(\begin{array} {c} -1 \\ x-3 \end{array}\right)=\left(\begin{array} {c} kx \\ 2k \end{array}\right)$$これより、$$~~~\biggl\{ \begin{eqnarray} ~-1=kx~~~\cdots{\Large ①} \\ ~x-3=2k~~~\cdots{\Large ②} \end{eqnarray}$$
②より、$$\hspace{ 10 pt}x-3=2k$$移項すると、$$\hspace{ 10 pt}x=2k+3~~~\cdots{\Large ③}$$これを①に代入すると、$$\hspace{ 10 pt}-1=k(2k+3)$$$$\hspace{ 10 pt}-1=2k^2+3k$$両辺を入れ替えて、移項すると、$$\hspace{ 28 pt}2k^2+3k=-1$$$$\hspace{ 10 pt}2k^2+3k+1=0$$たすき掛けの表より、
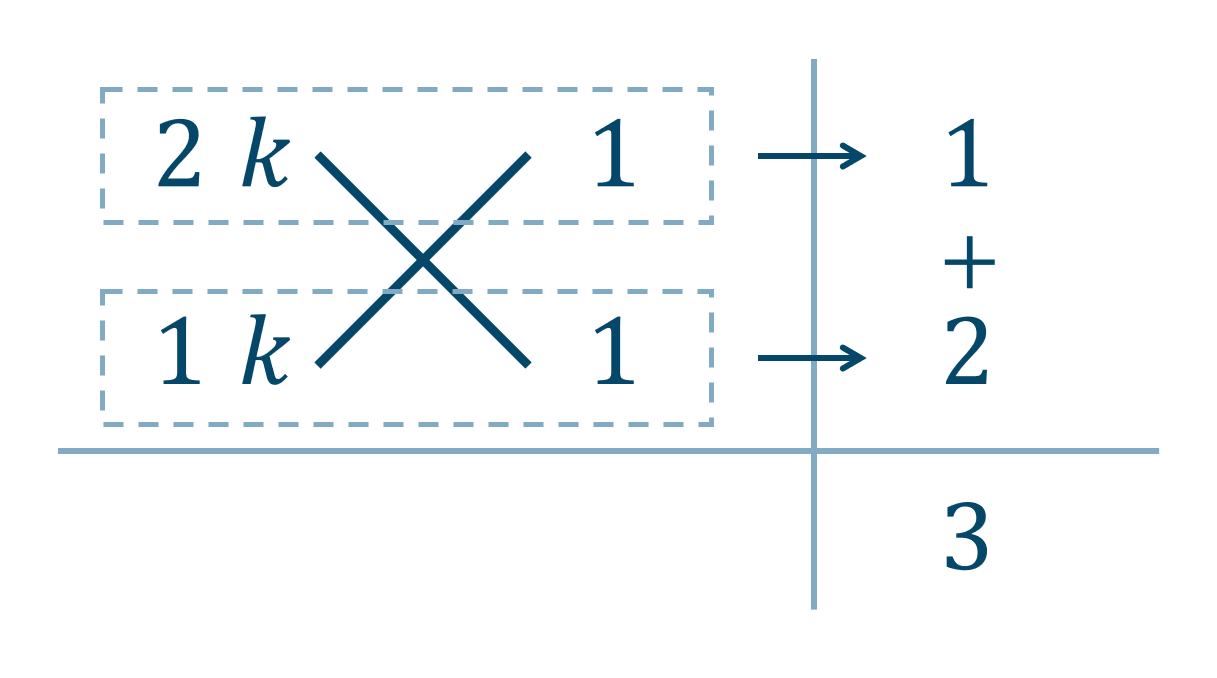
( ⅰ ) \(k=-1\) のとき、③より、$$\hspace{ 10 pt}x=2(-1)+3$$$$\hspace{ 18 pt}=-2+3$$$$\hspace{ 18 pt}=1$$
( ⅱ ) \(k=-{\large \frac{1}{2}}\) のとき、③より、$$\hspace{ 10 pt}x=2\left(-\frac{1}{2}\right)+3$$$$\hspace{ 18 pt}=-1+3$$$$\hspace{ 18 pt}=2$$
よって、答えは$$~~~x=1~,~2$$となります。
今回のまとめ
ベクトルの成分と平行条件は、向きが等しくなることから実数倍の条件式を用いて計算していきましょう。また、向きが反対の逆ベクトルでも平行となる点には注意しましょう。



