ベクトルの内積
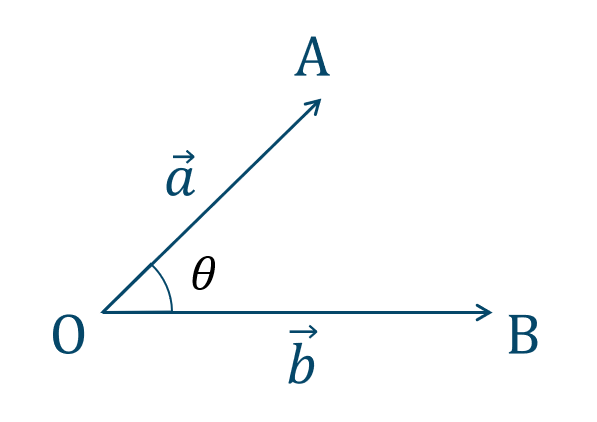
この２つのベクトルのなす角を$$~~~\theta~~~(0^\circ≦\theta≦180^\circ)$$としたとき、
\(\overrightarrow{a}\cdot\overrightarrow{b}\) を \(\overrightarrow{a}\) と \(\overrightarrow{b}\) の内積といい次の式で表します。
問題解説：ベクトルの内積①（基本）
問題解説(1)
\({\small (1)}\) \(|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4\) として、\(\overrightarrow{a}\) と \(\overrightarrow{b}\) のなす角が \(\theta\) が以下の値のとき、内積 \(\overrightarrow{a}\cdot\overrightarrow{b}\) を求めよ。$$~{\large ①}~\theta=30^\circ~~~~~~~~{\large ②}~\theta=60^\circ$$$$~{\large ③}~\theta=90^\circ~~~~~~~~{\large ④}~\theta=135^\circ$$
$${\large ①}~\theta=30^\circ$$\(|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4~,~\theta=30^\circ\) より、$$~~~~~~\overrightarrow{a}\cdot\overrightarrow{b}$$$$~=3\cdot4\cdot\cos{30^\circ}$$$$~=3\cdot4\cdot\frac{\sqrt{3}}{2}$$$$~=6\sqrt{3}$$
よって、答えは \(6\sqrt{3}\) となります。
$${\large ②}~\theta=60^\circ$$\(|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4~,~\theta=60^\circ\) より、$$~~~~~~\overrightarrow{a}\cdot\overrightarrow{b}$$$$~=3\cdot4\cdot\cos{60^\circ}$$$$~=3\cdot4\cdot\frac{1}{2}$$$$~=6$$
よって、答えは \(6\) となります。
$${\large ③}~\theta=90^\circ$$\(|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4~,~\theta=90^\circ\) より、$$~~~~~~\overrightarrow{a}\cdot\overrightarrow{b}$$$$~=3\cdot4\cdot\cos{90^\circ}$$$$~=3\cdot4\cdot0$$$$~=0$$
よって、答えは \(0\) となります。
$${\large ④}~\theta=135^\circ$$\(|\overrightarrow{a}|=3~,~|\overrightarrow{b}|=4~,~\theta=135^\circ\) より、$$~~~~~~\overrightarrow{a}\cdot\overrightarrow{b}$$$$~=3\cdot4\cdot\cos{135^\circ}$$$$~=3\cdot4\cdot\left(-\frac{1}{\sqrt{2}}\right)$$$$~=-12\cdot\frac{1}{\sqrt{2}}\cdot\frac{\sqrt{2}}{\sqrt{2}}$$$$~=-12\cdot\frac{\sqrt{2}}{2}$$$$~=-6\sqrt{2}$$
よって、答えは \(-6\sqrt{2}\) となります。
問題解説(2)
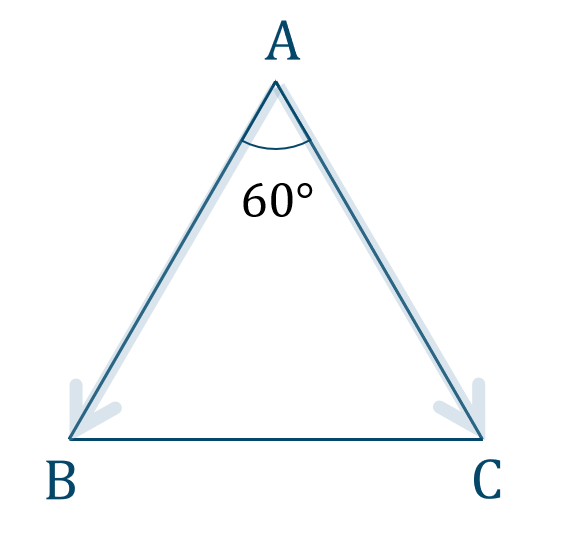
$${\large ①}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}$$図で表すと、次のようになります。
\(|\overrightarrow{\rm AB}|=3~,~|\overrightarrow{\rm AC}|=3\) で \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AC}\) のなす角が \(60^\circ\) となるので、内積は$$~~~~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}$$$$~=|\overrightarrow{\rm AB}|\cdot|\overrightarrow{\rm AC}|\cdot\cos{60^\circ}$$$$~=3\cdot3\cdot\frac{1}{2}$$$$~=\frac{9}{2}$$
よって、答えは$$~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AC}=\frac{9}{2}$$となります。
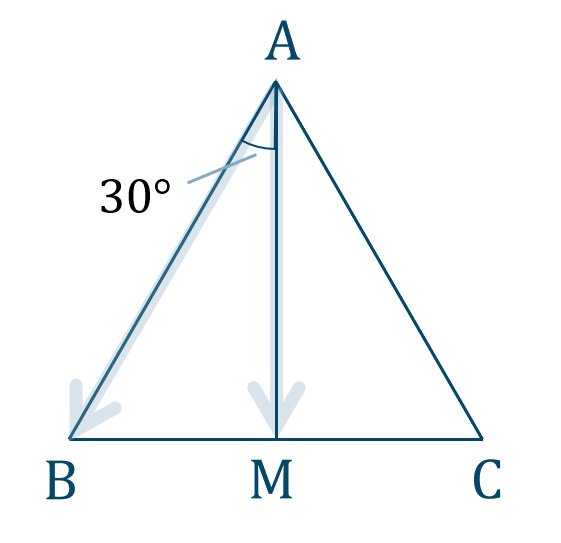
$${\large ②}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AM}$$図で表すと、次のようになります。
\(|\overrightarrow{\rm AB}|=|\overrightarrow{\rm BC}|=|\overrightarrow{\rm CA}|=3\) より、$$~~~|\overrightarrow{\rm AM}|=\frac{3\sqrt{3}}{2}$$また、$$~~~\angle{\rm BAM}=60^\circ\div2=30^\circ$$やって、 \(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm AM}\) のなす角が \(30^\circ\) となるので、内積は$$~~~~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AM}$$$$~=|\overrightarrow{\rm AB}|\cdot|\overrightarrow{\rm AM}|\cdot\cos{30^\circ}$$$$~=3\cdot\frac{3\sqrt{3}}{2}\cdot\frac{\sqrt{3}}{2}$$$$~=\frac{9\cdot3}{4}$$$$~=\frac{27}{4}$$
よって、答えは$$~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm AM}=\frac{27}{4}$$となります。
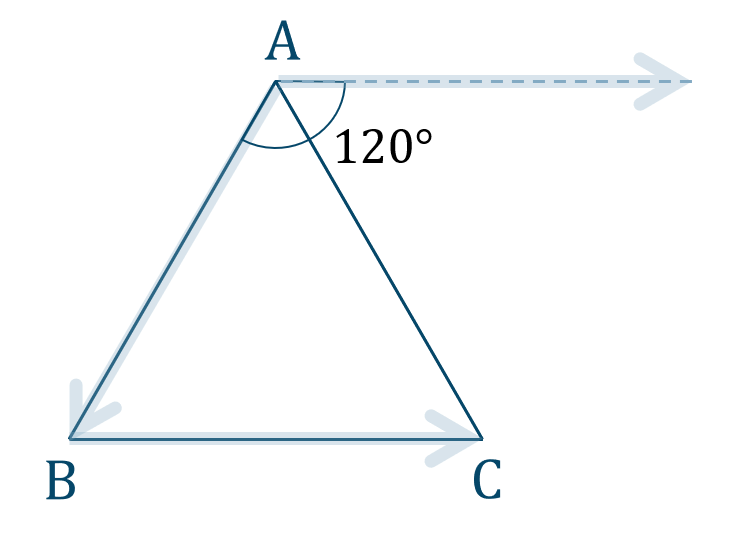
$${\large ③}~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BC}$$始点を揃えて図示すると、
これより、\(\overrightarrow{\rm AB}\) と \(\overrightarrow{\rm BC}\) のなす角が \(120^\circ\) となるので、内積は$$~~~~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BC}$$$$~=|\overrightarrow{\rm AB}|\cdot|\overrightarrow{\rm BC}|\cdot\cos{120^\circ}$$$$~=3\cdot3\cdot\left(-\frac{1}{2}\right)$$$$~=-\frac{9}{2}$$
よって、答えは$$~~~\overrightarrow{\rm AB}\cdot\overrightarrow{\rm BC}=-\frac{9}{2}$$となります。
$${\large ④}~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm BC}$$図で表すと、次のようになります。
$$~~~|\overrightarrow{\rm BM}|=\frac{1}{2}|\overrightarrow{\rm BC}|=\frac{3}{2}$$また、\(\overrightarrow{\rm BM}\) と \(\overrightarrow{\rm BC}\) のなす角が \(0^\circ\) となるので、内積は$$~~~~~~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm BC}$$$$~=|\overrightarrow{\rm BM}|\cdot|\overrightarrow{\rm BC}|\cdot\cos{0^\circ}$$$$~=\frac{3}{2}\cdot3\cdot1$$$$~=\frac{9}{2}$$
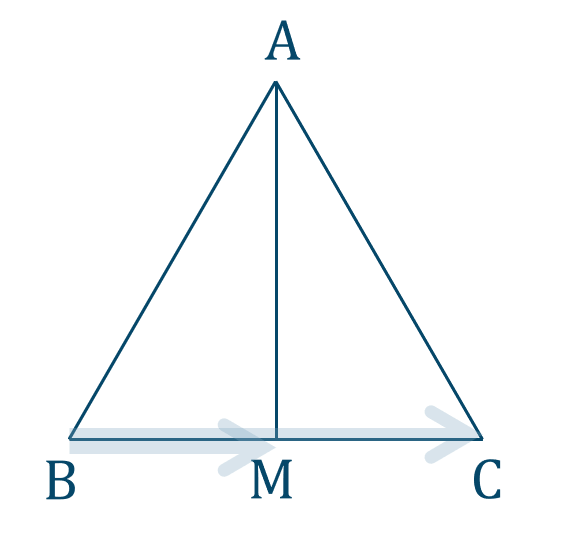
よって、答えは$$~~~\overrightarrow{\rm BM}\cdot\overrightarrow{\rm BC}=\frac{9}{2}$$となります。
今回のまとめ
ベクトルの内積で一番重要な点は、「始点を揃えてなす角を考える」ことです。なす角を求めるときに注意しましょう。
