【新課程】数研出版：高等学校数学Ⅲ[709]

p.102 練習1$${\small (1)}~y=-4x-8$$$${\small (2)}~y=x$$

p.103 練習2$${\small (1)}~y=\frac{\,1\,}{\,2\,}x+\frac{\,3\,}{\,2\,}$$$${\small (2)}~y=-\frac{\,2\sqrt{3}\,}{\,3\,}x+\frac{\,1\,}{\,2\,}+\frac{\,\sqrt{3}\pi\,}{\,9\,}$$

p.104 練習3$${\small (1)}~y=x+1$$$${\small (2)}~y=e^2x-e^2$$

p.105 練習4$${\small (1)}~y=2x+4$$$${\small (2)}~y=-\sqrt{2}x+1$$

p.107 練習5$$~~~c=1$$

p.107 練習6[証明] \(f(x)=e^x\) とおくと、\(f'(x)=e^x\)
\(f(x)\) はすべて実数 \(x\) で連続で微分可能であるから、平均値の定理より、$$~~~\frac{\,e^b-e^a\,}{\,b-a\,}=e^c~,~a< c < b$$これを満たす実数 \(c\) が存在する
ここで、\(f(x)\) は単調増加するので \(e^a< e^c < e^b\) となり、$$~~~e^a< \frac{\,e^b-e^a\,}{\,b-a\,} < e^b$$[終]

p.108 練習7閉区間 \([a~,~b]\) において、\(a≦u < v≦b\) を満たす任意の \(u~,~v\) をとると、平均値の定理より、$$~~~f(v)-f(u)=(v-u)f'(c)~,~u< c< v$$これを満たす実数 \(c\) が存在する
 
２
[証明] \(v-u>0~,~f'(c)<0\) より、$$~~~f(v)-f(u)< 0$$これより、\(f(u)> f(v)\) であるので、閉区間 \([a~,~b]\) で単調減少 [終]
 
３
[証明] \(f'(c)=0\) より、$$\begin{eqnarray}~~~f(v)-f(u)&=&0\\[2pt]~~~f(u)&=&f(v)\end{eqnarray}$$\(a≦u < v≦b\) を満たす任意の \(u~,~v\) に対して \(f(u)=f(v)\) であるので、閉区間 \([a~,~b]\) で定数 [終]

p.109 練習8[証明] \(F(x)=g(x)-f(x)\) とすると、
　\(F'(x)=g'(x)-f'(x)\)
これより、区間 \((a~,~b)\) で常に \(g'(x)=f'(x)\) ならば \(F'(x)=0\)
したがって、\(F(x)\) は区間 \([a~,~b]\) で連続で、 \(C\) を定数として
　\(F(x)=C\)
よって、
　\(g(x)-f(x)=C\)
したがって、閉区間 \([a~,~b]\) で
　 \(g(x)=f(x)+C\)
ただし \(C\) は定数 [終]

p.109 練習9\({\small (1)}~\)区間 \(x≦0\) で単調増加
　　区間 \(0≦x\) で単調減少
\({\small (2)}~\)区間 \(1≦x\) で単調増加
　　区間 \(0< x≦1\) で単調減少
\({\small (3)}~\)区間 \(0≦x≦\pi\) で単調増加

p.111 練習10\({\small (1)}~\)
　\(x=2\) で極大値 \({\large \frac{\,4\,}{\,e^2\,}}\)
　\(x=0\) で極小値 \(0\)
\({\small (2)}~\)
　\(x={\large \frac{\,1\,}{\,e\,}}\) で極小値 \(-{\large \frac{\,1\,}{\,e\,}}\)
\({\small (3)}~\)
　\(x=-\sqrt{2}\) で極大値 \(-2\sqrt{2}\)
　\(x=\sqrt{2}\) で極小値 \(2\sqrt{2}\)

p.112 練習11\({\small (1)}~\)
　\(x=-{\large \frac{\,1\,}{\,2\,}}\) で極大値 \({\large \frac{\,1\,}{\,4\,}}\)
　\(x=0\) で極小値 \(0\)
\({\small (2)}~\)
　\(x=-{\large \frac{\,4\,}{\,3\,}}\) で極大値 \({\large \frac{\,4\sqrt{6}\,}{\,9\,}}\)
　\(x=0\) で極小値 \(0\)

p.113 練習12$$~~~a=1$$　\(x=-1\) で極大値 \(-2\)
　\(x=1\) で極小値 \(2\)

p.114 練習13\({\small (1)}~\)
　\(x={\large \frac{\,\pi\,}{\,3\,}}\) で最大値 \({\large \frac{\,3\sqrt{3}\,}{\,4\,}}\)
　\(x={\large \frac{\,5\,}{\,3\,}}\pi\) で最小値 \(-{\large \frac{\,3\sqrt{3}\,}{\,4\,}}\)
\({\small (2)}~\)
　\(x=1\) で最大値 \({\large \frac{\,1\,}{\,2\,}}\)
　\(x=3\) で最小値 \(-{\large \frac{\,1\,}{\,2\,}}\)

p.117 練習14\({\small (1)}~\)
　\(x< -1~,~0< x\) で下に凸
　\(-1< x < 0\) で上に凸
　変曲点 \((-1~,~0)~,~(0~,~1)\)
\({\small (2)}~\)
　\(x< 2\) で上に凸
　\(2< x\) で下に凸
　変曲点 \(\left(2~,~{\large \frac{\,2\,}{\,e^2\,}}\right)\)
\({\small (3)}~\)
　\(0< x < {\large \frac{\,\pi\,}{\,2\,}}\) で下に凸
　\({\large \frac{\,\pi\,}{\,2\,}}< x < \pi\) で上に凸
　変曲点 \(\left({\large \frac{\,\pi\,}{\,2\,}}~,~{\large \frac{\,\pi\,}{\,2\,}}\right)\)
\({\small (4)}~\)
　常に上に凸
　変曲点なし

p.118 練習15

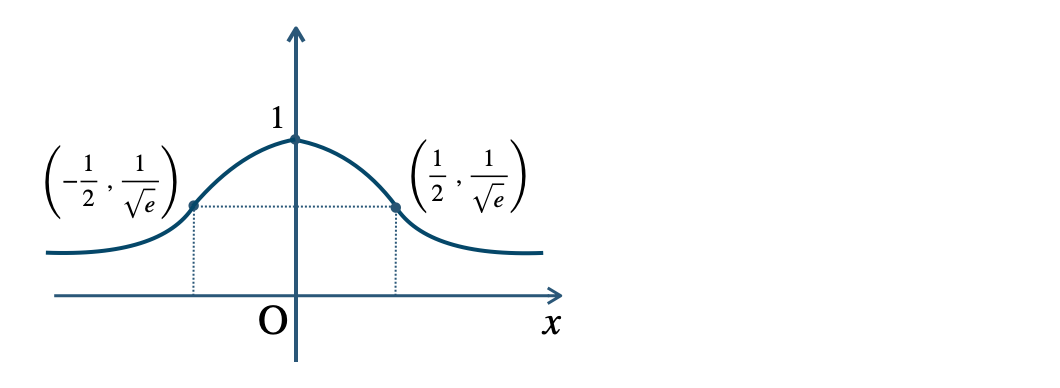
p.119 練習16

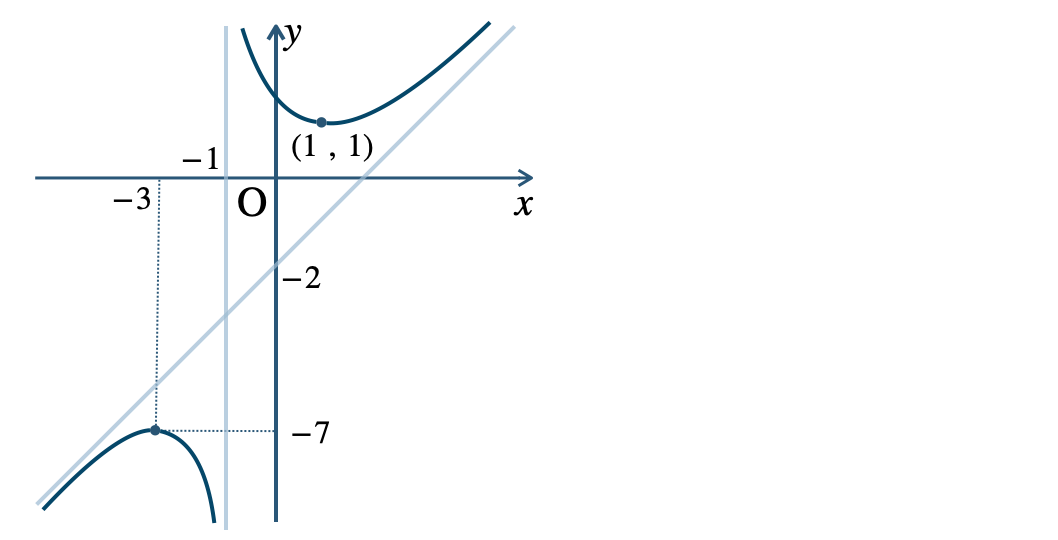
p.123 練習17\({\small (1)}~\)
　\(x=0\) で極大値 \(5\)
　\(x=\pm \sqrt{3}\) で極小値 \(-4\)
\({\small (2)}~\)
　\(x={\large \frac{\,2\,}{\,3\,}}\pi\) で極大値 \({\large \frac{\,2\,}{\,3\,}}\pi+\sqrt{3}\)
　\(x={\large \frac{\,4\,}{\,3\,}}\pi\) で極小値 \({\large \frac{\,4\,}{\,3\,}}\pi-\sqrt{3}\)

p.124 問題 2\({\small (1)}~\)[証明] \(y^2=4px\) 上の点 \((x_1~,~y_1)\) より、$$~~~y_1^2=4px_1$$また、\(y^2=4px\) の両辺を \(x\) で微分すると、$$~~~2y\cdot y’=4p$$\(y\neq 0\) のとき、$$~~~y’=\frac{\,2p\,}{\,y\,}$$よって、傾きは \({\large \frac{\,2p\,}{\,y_1\,}}\) となり、\(y_1\neq 0\) での接線の方程式は、$$~~~y-y_1=\frac{\,2p\,}{\,y_1\,}(x-x_1)$$\(y_1^2=4px_1\) を代入すると、$$\begin{eqnarray}~~~y_1y-4px_1&=&2p(x+x_1)\\[2pt]~~~y_1y&=&2p(x+x_1)\end{eqnarray}$$また、\(y=0\) のとき接点が \((0~,~0)\) となり接線が \(x=0\)
これは \((x_1~,~y_1)=(0~,~0)\) のとき上の式を満たす
以上より、接線の方程式は \(y_1y=2p(x+x_1)\) [終]
 
\({\small (2)}~\)[証明] 楕円上の点 \((x_1~,~y_1)\) より、$$~~~\frac{\,{x_1}^2\,}{\,a^2\,}+\frac{\,{y_1}^2\,}{\,b^2\,}=1~~~\cdots{\large ①}$$また、両辺を \(x\) で微分すると、$$~~~\frac{\,2x\,}{\,a^2\,}+\frac{\,2y\,}{\,b^2\,}y’=0$$\(y\neq 0\) のとき、$$~~~y’=-\frac{\,b^2x\,}{\,a^2y\,}$$よって、接線の傾きは \(-{\large \frac{\,b^2x_1\,}{\,a^2y_1\,}}\) となるので \(y_1\neq 0\) での接線の方程式は、$$\begin{eqnarray}~~~y-y_1&=&-\frac{\,b^2x_1\,}{\,a^2y_1\,}(x-x_1)
\\[3pt]~~~\frac{\,b^2x_1\,}{\,a^2y_1\,}x+y&=&\frac{\,b^2x_1\,}{\,a^2y_1\,}x_1+y_1
\\[3pt]~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}&=&\frac{\,{x_1}^2\,}{\,a^2\,}+\frac{\,{y_1}^2\,}{\,b^2\,}\end{eqnarray}$$①を代入すると、$$~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}=1$$ここで、\(y_1=0\) のとき接点が \((\pm a~,~0)\) となり接線の方程式は \(x=\pm a\)
これは \((x_1~,~y_1)=(\pm a~,~0)\) のとき上の式を満たす
以上より、接線の方程式は$$~~~\frac{\,x_1x\,}{\,a^2\,}+\frac{\,y_1y\,}{\,b^2\,}=1$$[終]

p.124 問題 7

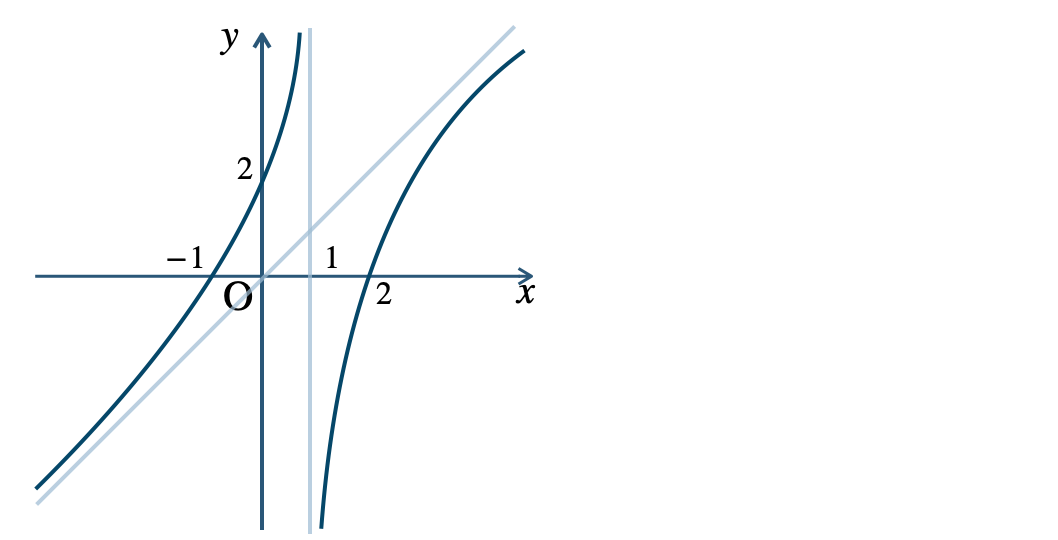
p.124 問題 8

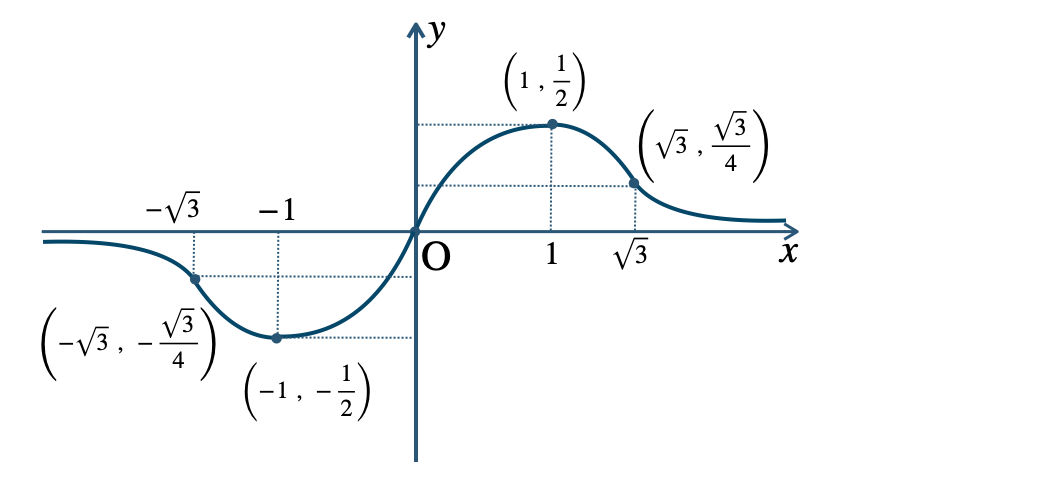
　\(x=1\) のとき、最大値 \({\large \frac{\,1\,}{\,2\,}}\)
　\(x=-1\) のとき、最大値 \(-{\large \frac{\,1\,}{\,2\,}}\)

p.125 練習18\({\small (1)}~\)[証明] \(f(x)=\log_{}(x+1)-x\) とすると、$$~~~f'(x)=\frac{\,1\,}{\,x+1\,}-1=-\frac{\,x\,}{\,x+1\,}$$\(x> 0\) のとき \(f'(x)< 0\) であるので、\(f(x)\) は \(x≧0\) で単調減少
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)< 0\)
したがって、\(x> 0\) で$$~~~\log_{}(x+1)< x$$[終]
 
\({\small (2)}~\)[証明] \(f(x)=e^x-\left(1+x+{\large \frac{\,x^2\,}{\,2\,}}\right)\) とすると、$$~~~f'(x)=e^x-(1+x)$$応用例題4より \(f'(x)=e^x-(1+x)> 0\)
よって、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~e^x > 1+x+\frac{\,x^2\,}{\,2\,}$$[終]

p.126 練習19\({\small (1)}~\)
　\(a> {\large \frac{\,27\,}{\,4\,}}\) のとき、３個
　\(a= {\large \frac{\,27\,}{\,4\,}}\) のとき、２個
　\(a< {\large \frac{\,27\,}{\,4\,}}\) のとき、１個
\({\small (2)}~\)
　\(-{\large \frac{\,1\,}{\,e\,}} < a< 0\) のとき、２個
　\(a≧0~,~a=-{\large \frac{\,1\,}{\,e\,}}\) のとき、１個
　\(a< -{\large \frac{\,1\,}{\,e\,}}\) のとき、０個

p.128 練習20　速度 \(v_0-gt~~[{\rm m/s}]\)
　加速度 \(-g~~[{\rm m/s^2}]\)

p.130 練習21\({\small (1)}~\)
　速さ \(2\sqrt{2}\)、加速度の大きさ \(2\)
\({\small (2)}~\)
　速さ \(2\pi\)、加速度の大きさ \(2\pi ^2\)

p.132 練習22$${\small (1)}~\cos{(a+h)}≒\cos{a}-h\sin{a}$$$${\small (2)}~\tan{(a+h)}≒\tan{a}+\frac{\,h\,}{\,\cos^2{a}\,}$$

p.132 練習23$${\small (2)}~e^x≒1+x$$$${\small (2)}~\log_{}(1+x)≒x$$$${\small (3)}~\frac{\,1\,}{\,1+x\,}≒1-x$$

p.140 練習26$${\small (1)}~1.0075$$$${\small (2)}~0.01$$$${\small (3)}~1.002$$

p.133 問題 9[証明] \(f(x)=\log_{}(1+x)-x+{\large \frac{\,x^2\,}{\,2\,}}\) とすると、$$~~~f'(x)=\frac{\,1\,}{\,1+x\,}-1+x=\frac{\,x^2\,}{\,1+x\,}$$\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~x-\frac{\,x^2\,}{\,2\,}< \log_{}(1+x)$$[終]

p.134 章末問題Ａ 2[証明] \(f(x)=\log_{}x\) とおくと、\(f'(x)={\large \frac{\,1\,}{\,x\,}}\)
\(f(x)\) は \(x> 0\) で連続で微分可能であるから、平均値の定理より、$$~~~\frac{\,\log_{}(a+1)-\log_{}a\,}{\,(a+1)-a\,}=\frac{\,1\,}{\,c\,}$$$$~~~a< c < a+1$$これを満たす実数 \(c\) が存在する
ここで、\(f(x)\) は \(x> 0\) 単調減少するので、\(a< c < a+1\) より、$$~~~\frac{\,1\,}{\,a+1\,} < \frac{\,1\,}{\,c\,} < \frac{\,1\,}{\,a\,}$$したがって、$$~~~\frac{\,1\,}{\,a+1\,} < \log_{}(a+1)-\log_{}a < \frac{\,1\,}{\,a\,}$$[終]

p.134 章末問題Ａ 4\({\small (1)}~\)

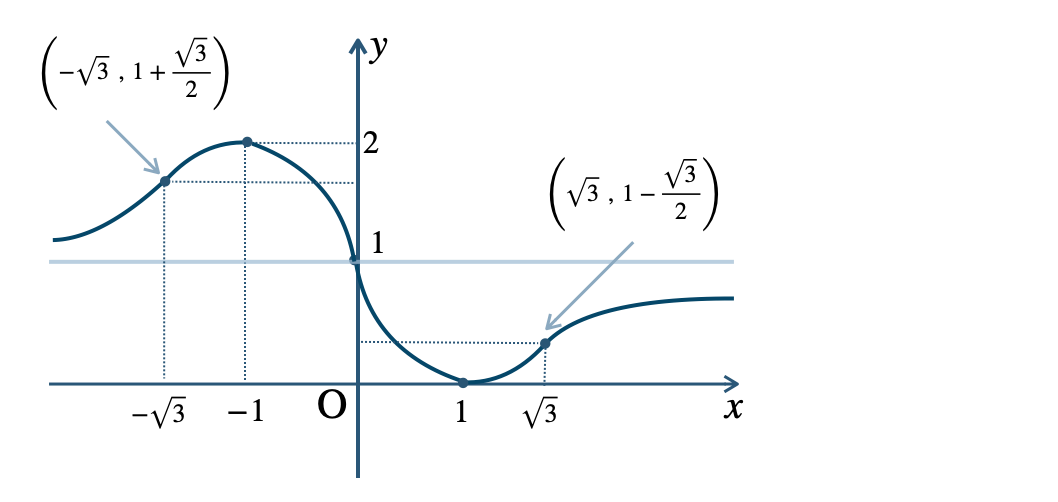
\({\small (2)}~\)

p.134 章末問題Ａ 5[証明] 図より、$$~~~{\rm AB=AC}=2r\cos{\theta}~,~{\rm BC}=2r\sin{2\theta}$$よって、周の長さは、$$~~~l=4r\cos{\theta}+2r\sin{2\theta}$$ただし、\(0< \theta < {\large \frac{\,\pi\,}{\,2\,}}\)\(\theta\) で微分すると、$$\begin{eqnarray}~~~\frac{\,dl\,}{\,d\theta\,}&=&-4r\sin{\theta}+4r\cos{2\theta}\\[3pt]~~~&=&-4r\sin{\theta}+4r(1-2\sin^2{\theta})\\[2pt]~~~&=&-4r(2\sin{\theta}-1)(\sin{\theta}+1)\end{eqnarray}$$\(\sin{\theta}+1 >0\) より、\({\large \frac{\,dl\,}{\,d\theta\,}}=0\) となるのは、$$~~~\sin{\theta}=\frac{\,1\,}{\,2\,}~\Leftrightarrow~\theta=\frac{\,\pi\,}{\,6\,}$$これより、増減表は、

\(\theta\)	\(0\)	\(\cdots\)	\({\large \frac{\,\pi\,}{\,6\,}}\)	\(\cdots\)	\({\large \frac{\,\pi\,}{\,2\,}}\)
\(l’\)		\(+\)	\(0\)	\(-\)
\(l\)		↗︎		↘︎

これより、\(\theta={\large \frac{\,\pi\,}{\,6\,}}\) で最大となる
このとき、\(\angle{\rm A}={\large \frac{\,\pi\,}{\,3\,}}\) の二等辺三角形となるので、\(\triangle {\rm ABC}\) は正三角形 [終]

p.134 章末問題Ａ 7\({\small (1)}~\)[証明] \(f(x)=\cos{x}-1+{\large \frac{\,x^2\,}{\,2\,}}\) とすると、$$~~~f'(x)=-\sin{x}+x$$$$~~~f”(x)=-\cos{x}+1$$\(f”(x)=0\) となるのは \(x=2\pi k\) ( \(k\) は整数 )のときで、それ以外では \(f”(x)> 0\)
よって、\(f'(x)\) は単調増加
また、\(f'(0)=0\) である
これより、\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~\cos{x}> 1-\frac{\,x^2\,}{\,2\,}$$[終]
 
\({\small (2)}~\)[証明] \(f(x)=\sin{x}-x+{\large \frac{\,x^3\,}{\,6\,}}\) とすると、$$~~~f'(x)=\cos{x}-1+\frac{\,x^2\,}{\,2\,}$$\(x> 0\) のとき \(f'(x)> 0\) であるので、\(f(x)\) は \(x≧0\) で単調増加
また、\(f(0)=0\) であるので \(x> 0\) のとき \(f(x)> 0\)
したがって、\(x> 0\) で$$~~~\sin{x} > x-\frac{\,x^3\,}{\,6\,}$$[終]

p.135 章末問題Ｂ 8[証明] 点 \({\rm P}\) の座標を \((t~,~\sqrt{t})\) ただし、\(t> 0\) とすると、
\(f(x)=\sqrt{x}\) として、\(f'(x)={\large \frac{\,1\,}{\,2\sqrt{x}\,}}\)
これより、法線の方程式は、$$\begin{eqnarray}~~~y-\sqrt{t}&=&-2\sqrt{t}(x-t)\\[2pt]~~~y&=&-2\sqrt{t}x+(2t+1)\sqrt{t}\end{eqnarray}$$これより、\(x\) 軸と交わる点 \({\rm Q}\) の \(x\) 座標は \(y=0\) より、$$~~~x=\frac{\,2t+1\,}{\,2\,}$$また、点 \({\rm R}(t~,~0)\) より、$$~~~{\rm QR}=\frac{\,2t+1\,}{\,2\,}-t=\frac{\,1\,}{\,2\,}$$したがって、線分 \({\rm QR}\) の長さは一定 [終]

p.135 章末問題Ｂ 11[証明]$$~~~f'(x)=3x^2+6ax+3b$$$$~~~f'{}'(x)=6x+6a$$\(f'{}'(x)=0\) より、\(x=-a\)
よって、変曲点Ａは \((-a~,~2a^3-3ab+c)\)
ここで、Ｃのグラフを点Ａが原点に重なるように平行移動させるとそのグラフは、$$~~~g(x)=x^3+3(b-a^2)x$$ここで、$$~~~g(-x)=-x^3-3(b-a^2)x=-g(x)$$となるので、\(g(x)\) は原点に関して対称である
したがって、曲線Ｃ上にＡ以外の任意の点Ｐをとり、Ａに関して対称な点をＱとすると、Qも曲線Ｃ上にある [終]