【新課程】数研出版：高等学校数学Ⅲ[709]

p.139 練習1\(C\) を積分定数とする$${\small (1)}~-\frac{\,1\,}{\,2x^2\,}+C$$$${\small (2)}~\frac{\,3\,}{\,4\,}x^{\frac{\,4\,}{\,3\,}}+C$$$${\small (3)}~\frac{\,2\,}{\,5\,}x^{\frac{\,5\,}{\,2\,}}+C=\frac{\,2\,}{\,5\,}x^2\sqrt{x}+C$$$${\small (4)}~2\sqrt{x}+C$$

p.140 練習2\(C\) を積分定数とする$${\small (1)}~\log_{}|x|+\frac{\,4\,}{\,x\,}-\frac{\,1\,}{\,2x^2\,}+C$$$${\small (2)}~\frac{\,2\,}{\,3\,}x\sqrt{x}+4\sqrt{x}+C$$$${\small (3)}~y-4\sqrt{y}+\log_{}y+C$$$${\small (4)}~\frac{\,9\,}{\,5\,}t^5-3t^2-\frac{\,1\,}{\,t\,}+C$$

p.141 練習3\(C\) を積分定数とする$${\small (1)}~\sin{x}+2\cos{x}+C$$$${\small (2)}~2\sin{x}-\tan{x}+C$$$${\small (3)}~-\frac{\,1\,}{\,\tan{x}\,}-x+C$$$${\small (4)}~\frac{\,5^x\,}{\,\log_{}5\,}+C$$$${\small (5)}~\frac{\,3^x\,}{\,\log_{}3\,}-2e^x+C$$

p.142 練習4\(C\) を積分定数とする$${\small (1)}~\frac{\,1\,}{\,15\,}(3x+1)^5+C$$$${\small (2)}~-\frac{\,1\,}{\,8\,}(4x-3)^{-2}+C$$$${\small (3)}~-\sqrt{1-2x}+C$$$${\small (4)}~\frac{\,1\,}{\,2\,}\log_{}|2x+1|+C$$$${\small (5)}~-\frac{\,1\,}{\,2\,}\cos{2x}+C$$$${\small (6)}~\frac{\,1\,}{\,3\,}e^{3x-1}+C$$

p.144 練習5\(C\) を積分定数とする$${\small (1)}~\frac{\,1\,}{\,15\,}(3x+1)(2x-1)\sqrt{2x-1}+C$$$${\small (2)}~\frac{\,2\,}{\,3\,}(x-2)\sqrt{x+1}+C$$

p.145 練習6\(C\) を積分定数とする$${\small (1)}~\frac{\,2\,}{\,9\,}(x^3+2)\sqrt{x^3+2}+C$$$${\small (2)}~\frac{\,1\,}{\,4\,}\sin^4{x}+C$$$${\small (3)}~\frac{\,1\,}{\,2\,}(\log_{}x)^2+C$$

p.145 練習7\(C\) を積分定数とする$${\small (1)}~\log_{}|x^2+x-1|+C$$$${\small (2)}~\log_{}(e^x+1)+C$$$${\small (3)}~\log_{}|\sin{x}|+C$$

p.146 練習8\(C\) を積分定数とする$${\small (1)}~-x\cos{x}+\sin{x}+C$$$${\small (2)}~-(x+1)e^{-x}+C$$

p.147 練習9\(C\) を積分定数とする$${\small (1)}~x\log_{}2x-x+C$$$${\small (2)}~x\log_{}x^2-2x+C$$$${\small (3)}~\frac{\,1\,}{\,2\,}x^2\log_{}x-\frac{\,1\,}{\,4\,}x^2+C$$

p.147 練習10\(C\) を積分定数とする$$~~~(1-x^2)\cos{x}+2x\sin{x}+C$$

p.148 練習11$$~~~a=-1~,~b=2$$\(C\) を積分定数とする$$~~~\log_{}\frac{\,(x+2)^2\,}{\,|x+1|\,}+C$$

p.148 練習12\(C\) を積分定数とする$${\small (1)}~\frac{\,1\,}{\,2\,}x^2-2x+3\log_{}|x+2|+C$$$${\small (2)}~x^2+x+\frac{\,1\,}{\,2\,}\log_{}|2x-1|+C$$$${\small (3)}~\log_{}\left| \frac{\,x-1\,}{\,x+2\,} \right|+C$$

p.149 練習13\(C\) を積分定数とする$${\small (1)}~\frac{\,1\,}{\,2\,}x+\frac{\,1\,}{\,4\,}\sin{2x}+C$$$${\small (2)}~\frac{\,1\,}{\,2\,}x-\frac{\,1\,}{\,12\,}\sin{6x}+C$$$${\small (3)}~-\frac{\,1\,}{\,4\,}\cos{2x}+C=\frac{\,1\,}{\,2\,}\sin^2{x}+C$$$${\small (4)}~\frac{\,1\,}{\,10\,}\sin{5x}+\frac{\,1\,}{\,2\,}\sin{x}+C$$$${\small (5)}~-\frac{\,1\,}{\,8\,}\sin{4x}+\frac{\,1\,}{\,4\,}\sin{2x}+C$$

p.151 練習14$${\small (1)}~\frac{\,1\,}{\,2\,}$$$${\small (2)}~1$$$${\small (3)}~-\log_{}2$$$${\small (4)}~\frac{\,3\,}{\,2\log_{}2\,}$$

p.152 練習15$${\small (1)}~\frac{\,2\,}{\,3\,}(3\sqrt{3}-2\sqrt{2})$$$${\small (2)}~10$$$${\small (3)}~0$$$${\small (4)}~0$$$${\small (5)}~\pi$$$${\small (6)}~\frac{\,2\,}{\,3\,}$$

p.153 練習16$${\small (1)}~2$$$${\small (2)}~e^2+\frac{\,1\,}{\,e\,}-3$$

p.155 練習17$${\small (1)}~\frac{\,1\,}{\,42\,}$$$${\small (2)}~\frac{\,256\,}{\,15\,}$$

p.155 練習18$${\small (1)}~\frac{\,\pi\,}{\,2\,}$$$${\small (2)}~\pi+\sqrt{3}$$$${\small (3)}~\frac{\,\pi\,}{\,6\,}$$

p.156 練習19$${\small (1)}~\frac{\,\pi\,}{\,3\,}$$$${\small (2)}~\frac{\,\pi\,}{\,4\,}$$

p.156 練習20　偶関数 ②
　奇関数 ①、③

p.157 練習21$${\small (1)}~36$$$${\small (2)}~0$$$${\small (3)}~0$$$${\small (4)}~\frac{\,\pi\,}{\,2\,}$$

p.158 練習22$${\small (1)}~\pi$$$${\small (2)}~1$$$${\small (3)}~2\log_{}2-\frac{\,3\,}{\,4\,}$$

p.158 練習23$$~~~-\frac{\,8\,}{\,5\,}$$

p.158 練習24$$~~~\pi-2$$

p.159 研究 練習1$$~~~\frac{\,e^{\frac{\,\pi\,}{\,2\,}}-1\,}{\,2\,}$$

p.161 練習25$${\small (1)}~\sin{x}$$$${\small (2)}~x\log_{}x$$

p.161 練習26$$~~~G'(x)=e^x-1~,~G'{}'(x)=e^x$$

p.162 練習27$$~~~9x\cos{3x}-x\cos{x}$$

p.162 練習28$$~~~f(x)=x+\frac{\,1\,}{\,2-e\,}$$

p.163 練習29[証明] $$\begin{eqnarray}~~~T_n&=&0\cdot\frac{\,1\,}{\,n\,}+\left(\frac{\,1\,}{\,n\,}\right)^2\cdot\frac{\,1\,}{\,n\,}\\[3pt]~~~&~&~~~~+\left(\frac{\,2\,}{\,n\,}\right)^2\cdot\frac{\,1\,}{\,n\,}+\cdots\\[3pt]~~~&~&~~~~~~\cdots+\left(\frac{\,n-1\,}{\,n\,}\right)^2\cdot\frac{\,1\,}{\,n\,}\\[3pt]~~~&=&\frac{\,1\,}{\,n^3\,}\{1^2+2^2+\cdots+(n-1)^2\}\\[3pt]~~~&=&\frac{\,1\,}{\,n^3\,}\sum_{k=1}^{n-1}k^2\\[3pt]~~~&=&\frac{\,1\,}{\,n^3\,}\cdot\frac{\,1\,}{\,6\,}(n-1)n(2n-1)\\[3pt]~~~&=&\frac{\,1\,}{\,6\,}\left(1-\frac{\,1\,}{\,n\,} \right)\left(2-\frac{\,1\,}{\,n\,} \right)\end{eqnarray}$$これより、$$~~~\lim_{n \to \infty}T_n=\frac{\,1\,}{\,6\,}(1-0)(2-0)=\frac{\,1\,}{\,3\,}=S$$[終]

p.165 練習30$$~~~\frac{\,1\,}{\,5\,}$$

p.166 練習31\({\small (1)}~\)[証明] \(x≧0\) のとき、$$~~~x+1≦x^2+x+1$$したがって、$$~~~\frac{\,1\,}{\,x+1\,}≧\frac{\,1\,}{\,x^2+x+1\,}$$[終]
 
\({\small (2)}~\)[証明] \({\small (1)}\) の不等式の等号は常には成り立たないので、$$~~~\int_{0}^{1} \frac{\,1\,}{\,x+1\,} dx > \int_{0}^{1} \frac{\,1\,}{\,x^2+x+1\,}dx$$ここで、$$~~\int_{0}^{1} \frac{\,1\,}{\,x+1\,} dx=\left[ \log_{}|x+1| \right]_{0}^{1}=\log_{}2$$したがって、$$~~~\log_{}2 > \int_{0}^{1} \frac{\,1\,}{\,x^2+x+1\,}dx$$[終]

p.167 練習32[証明] 自然数 \(k\) について、\(k≦x≦k+1\) とすると、$$~~~\frac{\,1\,}{\,k\,}≧\frac{\,1\,}{\,x\,}$$等号は常に成り立たないので、$$~~~\frac{\,1\,}{\,k\,}> \int_{k}^{k+1}\frac{\,1\,}{\,x\,}dx$$これより、\(n≧2\) のとき、$$~~~\sum_{k=1}^{n}\frac{\,1\,}{\,k\,}> \sum_{k=1}^{n}\int_{k}^{k+1}\frac{\,1\,}{\,x\,}dx$$左辺は、$$~~~\sum_{k=1}^{n}\frac{\,1\,}{\,k\,}=\frac{\,1\,}{\,2\,}+\frac{\,1\,}{\,3\,}+\cdots+\frac{\,1\,}{\,n\,}$$右辺は、$$\begin{split}&\sum_{k=1}^{n}\int_{k}^{k+1}\frac{\,1\,}{\,x\,}dx\\[3pt]~~=~&\int_{1}^{n+1}\frac{\,1\,}{\,x\,}dx\\[3pt]~~=~&\left[ \log_{}x \right]_{1}^{n+1}=\log_{}(n+1)\end{split}$$したがって、$$~~~1+\frac{\,1\,}{\,2\,}+\frac{\,1\,}{\,3\,}+\cdots+\frac{\,1\,}{\,n\,}> \log_{}(n+1)$$[終]

p.169 練習33$${\small (1)}~1$$$${\small (2)}~\frac{\,14\,}{\,3\,}$$

p.169 練習34$$~~~e^2-2e+1$$

p.170 練習35$${\small (1)}~\frac{\,1\,}{\,3\,}$$$${\small (2)}~\frac{\,15\,}{\,8\,}-2\log_{}2$$

p.171 練習36$${\small (1)}~\frac{\,14\,}{\,3\,}$$$${\small (2)}~\frac{\,125\,}{\,6\,}$$

p.172 練習37$$~~~\frac{\,\sqrt{2}\,}{\,4\,}\pi$$

p.173 練習38$$~~~3\pi$$

p.175 練習39[証明]

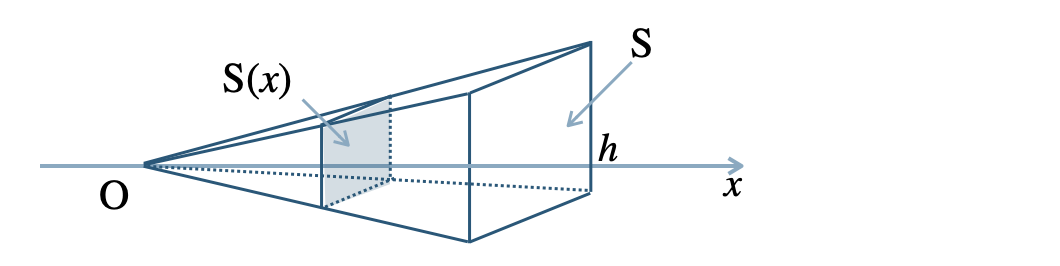
この角錐の頂点から底面に垂線を下ろし、これを \(x\) 軸として、頂点を原点にとる
座標が \(x\) である点を通り、\(x\) 軸に垂直な平面で角錐を切ったときの断面積を \(S(x)\) とする
この断面は底面と相似な多角形で。相似比は \(x:h\) であるから、面積比は２乗の比となり、$$~~~S(x):S=x^2:h^2$$これより、$$~~~S(x)=\frac{\,S\,}{\,h^2\,}x^2$$したがって、$$\begin{eqnarray}~~~V&=&\int_{0}^{h}\frac{\,S\,}{\,h^2\,}x^2 \,dx\\[3pt]~~~&=&\frac{\,S\,}{\,h^2\,}\left[ \frac{\,x^3\,}{\,3\,} \right]_{0}^{h}\\[3pt]~~~&=&\frac{\,S\,}{\,h^2\,}\cdot\frac{\,h^3\,}{\,3\,}\\[3pt]~~~&=&\frac{\,1\,}{\,3\,}Sh\end{eqnarray}$$[終]

p.176 練習40$$~~~\frac{\,2\,}{\,3\,}a^3$$

p.177 練習41$${\small (1)}~\frac{\,16\,}{\,15\,}\pi$$$${\small (2)}~\frac{\,1\,}{\,2\,}\pi^2$$

p.178 練習42$$~~~\frac{\,4\,}{\,3\,}\pi ab^2$$

p.178 練習43$${\small (1)}~\frac{\,9\,}{\,2\,}\pi$$$${\small (2)}~\frac{\,\pi\,}{\,5\,}$$

p.179 練習44$$~~~\frac{\,108\,}{\,5\,}\pi$$

p.180 練習45$$~~~\frac{\,8\,}{\,15\,}\pi$$

p.181 練習46$$~~~5$$

p.183 練習47$$~~~2$$

p.184 練習48$$~~~\sqrt{1+\pi^2}\left(1-\frac{\,1\,}{\,e^2\,} \right)$$

p.186 練習49$$~~~6$$

p.187 練習50$$~~~\frac{\,335\,}{\,27\,}$$

p.188 問題 15\({\small (1)}~\)[証明] 曲線上の任意の点 \((a~,~b)\) に対して、$$~~~b^2=a^2(1-a^2)$$ここで、\(x\) 軸に関して対称な点 \((a~,~-b)\) に対しても、$$~~~b^2=a^2(1-a^2)$$となり曲線上にある
したがって、この曲線は \(x\) 軸に関して対称である
また、\(y\) 軸に関して対称な点 \((-a~,~b)\) に対しても、$$~~~b^2=a^2(1-a^2)$$となり曲線上にある
したがって、この曲線は \(y\) 軸に関して対称である [終]$${\small (2)}~\frac{\,4\,}{\,3\,}$$

p.190 章末問題Ｂ 10[証明] \(\cos{x}=\sin{\left({\large \frac{\,\pi\,}{\,2\,}}-x\right)}\) として、\({\large \frac{\,\pi\,}{\,2\,}}-x=t\) とおくと、
\(x\) が \(0\to {\large \frac{\,\pi\,}{\,2\,}}\) のとき \(t\) は \({\large \frac{\,\pi\,}{\,2\,}} \to 0\)
また、 \(dx=-dt\) であるので、$$\begin{split}&\int_{0}^{\frac{\,\pi\,}{\,2\,}}f(\cos{x})dx\\[3pt]~~=~&\int_{0}^{\frac{\,\pi\,}{\,2\,}}f\left(\sin{\left( \frac{\,\pi\,}{\,2\,}- x \right)}\right)dx\\[3pt]~~=~&\int_{\frac{\,\pi\,}{\,2\,}}^{0}f(\sin{t})(-dt)\\[3pt]~~=~&\int_{0}^{\frac{\,\pi\,}{\,2\,}}f(\sin{t})dt\\[3pt]~~=~&\int_{0}^{\frac{\,\pi\,}{\,2\,}}f(\sin{x})dx\end{split}$$したがって、$$~~~\int_{0}^{\frac{\,\pi\,}{\,2\,}}f(\sin{x})dx=\int_{0}^{\frac{\,\pi\,}{\,2\,}}f(\cos{x})dx$$[終]

p.192 研究 練習1　\(y=Ae^{x^2}\)
ただし、\(A\) は任意の定数

p.193 研究 練習2　\(x^2-y^2=C\)
ただし、\(C\) は任意の定数